- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Уравнения, сводящиеся к квадратным
Содержание
- 2. Квадратное уравнение. Решение уравнений, сводящихся к квадратным, сводится к решению квадратных уравнений.
- 3. Существует ряд уравнений, которые удается решить при помощи сведения их к квадратным уравнениям.
- 4. Определение!!!Уравнение ах⁴+вх²+с=0, где а≠0,Называется биквадратным
- 5. Алгоритм решения биквадратного уравнения:
- 6. Образец решения:
- 7. 5. Выполним обратную замену
- 8. Общий знаменатель дробей (х+2)(х-3)Если х+2≠0 и
- 9. Преобразуем это уравнение:
- 10. Уравнение №2 +=(х-1)(х-2)≠0, отсюда следует1+3(х-2)=(3-х)(х-1). Преобразуем
- 11. Скачать презентацию
- 12. Похожие презентации
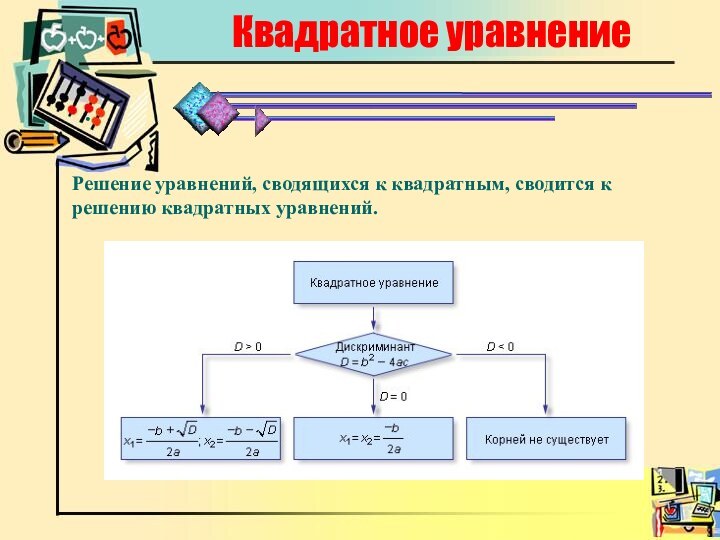
Квадратное уравнение. Решение уравнений, сводящихся к квадратным, сводится к решению квадратных уравнений.










Слайд 2
Квадратное уравнение
.
Решение уравнений, сводящихся к квадратным, сводится
к решению квадратных уравнений.
Слайд 3 Существует ряд уравнений, которые удается решить при помощи
сведения их к квадратным уравнениям.
Слайд 6
Образец решения:
1.Запишем
уравнение
9х⁴-32х²-16=0
2. Введем новую переменнуюПусть х²=t, t≥0
Тогда х⁴=t²
3. Запишем уравнение, используя новую переменную
9t²-32t-16=0
4. Решим квадратное уравнение
D=b²-4ac
D=(-32)²-4×9×(-16)=1024+576=1600
D˃0, два корня
t1=4; t2=-4/9-не удовлетворяет условию t≥0
Слайд 7
5. Выполним обратную замену
t=4,
значит х²=46.Решим полученное уравнение
х²=4
х=±√4
х=±2
7.Запишем ответ
Ответ:-2;2.
Слайд 8
Общий знаменатель дробей (х+2)(х-3)
Если х+2≠0 и х-3≠0
то, умножая обе части уравнения на
(х+2)(х-3), получаем
3(х-3)-4(х+2)=3(х+2)(х-3)
Уравнение №1
Слайд 9
Преобразуем это уравнение:
Зх-9-4х-8=3(х²-х-6)
-х-17=3х²-3х-183х²-2х-1=0
Решаем полученное квадратное уравнение:
х1=1; х2= ;
Т.к. при х1=1 и х2= знаменатели дробей исходного уравнения образующиеся в нуль, то числа 1 и является корнями исходного уравнения.
Ответ: х1=1; х2= .
Слайд 10
Уравнение №2
+
=
(х-1)(х-2)≠0, отсюда следует
1+3(х-2)=(3-х)(х-1). Преобразуем это уравнение
1+3х-6=х²+4х-3
х²-х-2=0
х=-1; х=2
при
х=-1 | (1-1)(1-2) ≠0
при х=2 | (2-1)(2-2)=0, поэтому число
2 не являеться корнем исходного уравненияответ:х=-1.