Кичкасс
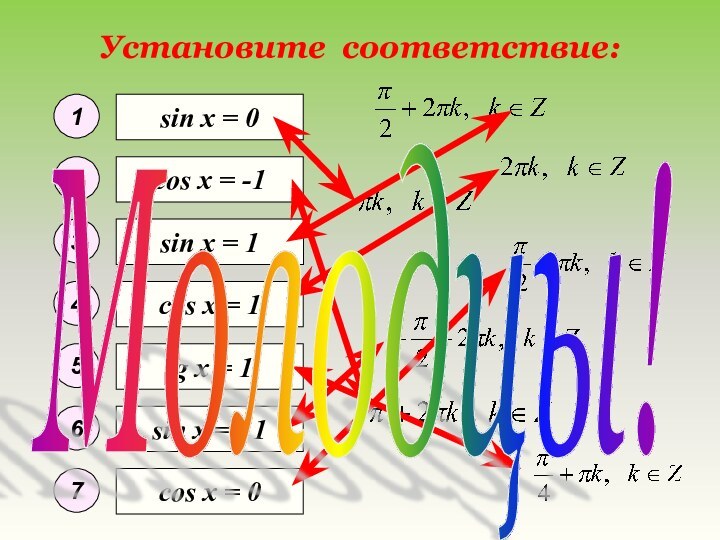
sin x = 1
cos x = 0
sin 4x –
sin 2x = 0Удачи!
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть















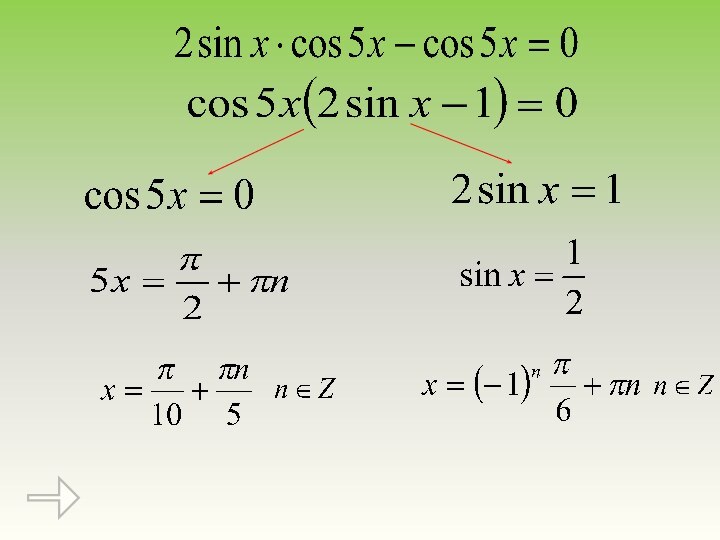


Удачи!
Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела.
Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников. Также следует отметить применение тригонометрии в таких областях, как техника навигации, теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, биология, медицина (включая ультразвуковое исследование (УЗИ) и компьютерную томографию), фармацевтика, химия, теория чисел (и, как следствие, криптография), сейсмология, метеорология, океанология, картография, многие разделы физики, топография и геодезия, архитектура, фонетика, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография.
Значительный вклад в развитие тригонометрии внесли арабские ученые Аль-Батани (850-929) и Абу-ль-Вефа Мухамед-бен Мухамед (940-998), который составил таблицы синусов и тангенсов через 10’ с точностью до 1/604. Теорему синусов уже знали индийский ученый Бхаскара (р. 1114, год смерти неизвестен) и азербайджанский астроном и математик Насиреддин Туси Мухамед (1201-1274). Кроме того, Насиреддин Туси в своей работе Трактат о полном четырехстороннике изложил плоскую и сферическую тригонометрию как самостоятельную дисциплину. Теорему тангенсов доказал Региомонтан (латинизированное имя немецкого астронома и математика Иоганна Мюллера (1436-1476)). Региомонтан составил также подробные тригонометрические таблицы; благодаря его трудам плоская и сферическая тригонометрия стала самостоятельной дисциплиной и в Европе. Дальнейшее развитие тригонометрия получила в трудах выдающихся астрономов Николая Коперника (1473-1543) – творца гелиоцентрической системы мира, Тихо Браге (1546-1601) и Иогана Кеплера (1571-1630), а также в работах математика Франсуа Виета (1540-1603), который полностью решил задачу об определениях всех элементов плоского или сферического треугольника по трем данным.
2. При каком значении а
уравнение cos x = a имеет
решение?
При каком значении а
уравнение sin x = a имеет
решение?
Какой формулой
выражается это решение?
Какой формулой
выражается это решение?
4.
На какой оси откладывается
значение а при решении
уравнения cos x = a ?
4.
На какой оси откладывается
значение а при решении
уравнения sin x = a ?
В каком промежутке
находится значение а?
6. В каком промежутке
находится значение а?
Каким будет решение
уравнения cos x = 1?
7. Каким будет решение
уравнения sin x = 1?
8. Каким будет решение
уравнения cos x = -1?
8. Каким будет решение
уравнения sin x = -1?
Чему равняется
arccos ( - a)?
10. Чему равняется
arcsin ( - a)?
В каком промежутке
находится arctg a?
11. В каком промежутке
находится arcctg a?
Какой формулой
выражается решение
уравнения tg x = а?
12. Какой формулой
выражается решение
уравнения сtg x = а?
cos x = 1
tg x = 1
cos x = -1
1
2
3
4
5
6
7
cos x = 1
tg x = 1
cos x = -1
1
2
3
4
5
6
7
Молодцы!
1.
2.
3.
4.
5.
6.
7.
8.
9.
10
А.
Б.
В.
Г.
Д.
Е.
Ж.
З.
И.
К.
Л.
М.
Корней нет
Вернёмся к подстановке, у нас получиться два уравнения
Решений нет, т.к
Ответ:
Решим пример методом разложения на множители