Слайд 3
В математике существует специальная операция, лежащая в основе
суждений о сходстве или различии объектов. Это — сравнение.
При ее помощи выявляются количественные и качественные характеристики объекта.
А можно измерить его красоту?
Слайд 4
В человеческой культуре создан специальный «инструмент» такого измерения.
Он носит название «божественная пропорция» или «золотое сечение»
Слайд 5
Цель работы:
Узнать, что же такое «золотое сечение»,
какое значение закон «золотого сечения» имеет в природе, искусстве,
в жизни человека
Слайд 6
Объект исследования:
Золотое сечение, объекты архитектуры нашего города,
бабочки, картины различных художников, история государств, участников Варшавского договора,
флаги этих государств
Слайд 7
Предмет исследования:
Отображение «Золотого сечения» природе, жизни и в
исторической деятельности человека
Слайд 8
Гипотеза:
Все красивое подчинено закону «золотого сечения»
Слайд 9
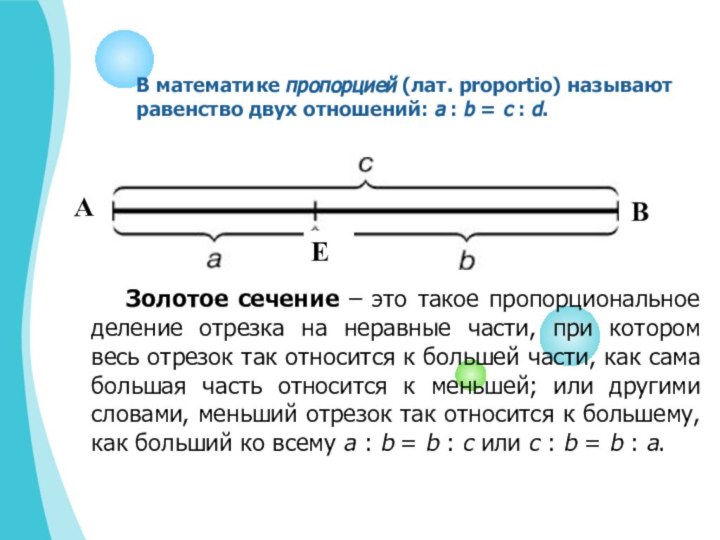
В математике пропорцией (лат. proportio) называют равенство двух
отношений: a : b = c : d.
Золотое сечение
– это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему a : b = b : c или с : b = b : а.
А
В
Е
Слайд 10
Отрезки золотой пропорции выражаются бесконечной иррациональной дробью: если
АВ принять за единицу, то ВE = 0,618..., АЕ
= 0,382...
Для практических целей часто используют приближенные значения 0,62 и 0,38.
Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям.
Слайд 12
Прямоугольник называется «золотым», если в нем отношение большей
стороны к меньшей равно золотой пропорции, то есть
АВ:
ВС = t = 1,618033988...
В данном прямоугольнике
a : b = 24,72 : 15,28
a : b = 1,617…
Он «золотой»
Слайд 13
Можно ли считать, что прямоугольник с отношением сторон,
равным t, выглядит изящнее, чем прямоугольники с отношением сторон,
скажем, 2:1, 3:2 или 5:7?
Впрочем, может ли прямоугольник сам по себе быть захватывающе прекрасным или отталкивающе безобразным?
Чтобы ответить на этот вопрос, были проведены специальные эксперименты.
Слайд 14
Собрали 60 рисунков прямоугольников.
Из них:
на 37 отношения
сторон соответствуют «золотым» размерам;
на 7 – 2:1;
остальные просто обвели
огрызки своих линеек.
Слайд 15
Вывод:
большинство людей интуитивно рисует прямоугольник, подчиняясь закону
золотого сечения
Слайд 17
Есть предположение, что используя закономерности золотого сечения, можно
исследовать пропорциональную структуру любого художественного произведения, даже если оно
создавалось на основе творческой интуиции.
Слайд 18
Мы провели исследования картин разных художников.
Художники оказались
гармонично развитыми людьми.
На 16 из 20 картин линия горизонта
проведена в отношении, близком к 1,7.
Слайд 19
Провели эксперимент в школе. Попросили одноклассников нарисовать линию
горизонта там, где они считают, что это будет красиво.
Собрали 32 рисунка.
Из них:
на 23 — линия горизонта делит лист А4 в отношении близком к 1,7;
на 6 — проведена ровно посередине;
на 3 — по разному (2:1, 1:3, 2:7)
Слайд 20
Вывод:
большинство людей интуитивно проводит линию горизонта, подчиняясь
закону «золотого сечения».
Слайд 22
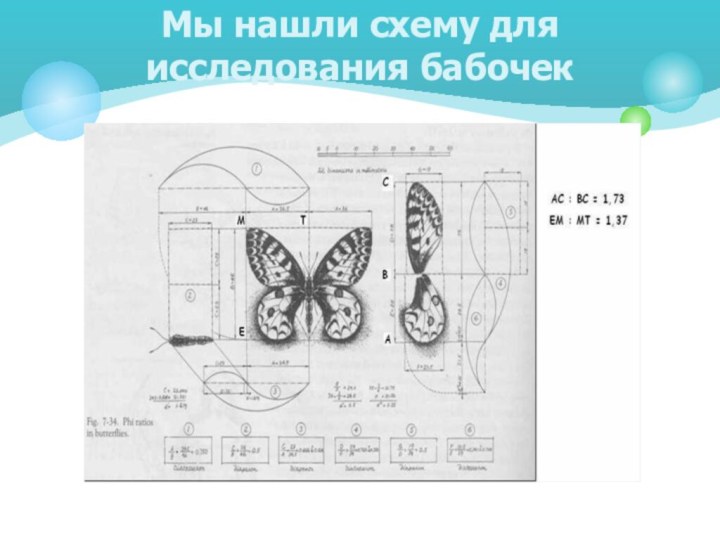
Мы нашли схему для исследования бабочек
Слайд 23
У учителя биологии одолжили все наглядные пособия с
бабочками и стрекозами.
Исследовали 22 бабочки.
Все бабочки отвечают «божественной пропорции».
Вывод:
закон «золотого сечения» в природе (в частности на бабочках) работает безукоризненно.
Слайд 24
«Золотое сечение»
в архитектуре
Слайд 25
«Для полной пропорциональной согласованности архитектурного памятника, представляющего собой
в любом случае объемное решение, требуется пропорциональное согласование прежде
всего его линейных размеров по высотам и горизонталям, следствием чего и является пропорциональное решение фасадных площадей и далее всего объема».
Г.Д. Гримм
Слайд 26
Сначала провели анкету, которая помогла определить красивые объекты.
Был опрошен 91 человек (ученики, родители и учителя школы).
Слайд 27
В результате эксперимента измерено 20 архитектурных объектов города.
Имеют
«золотые» пропорции — 11 зданий.
Слайд 28
Вывод:
архитекторы, проектирующие здания нашего города, придерживаются «законов
красоты» — применяют «золотое сечение». Здания, получившие высокие рейтинги
при опросе имеют «золотые» элементы в своей конструкции.
Слайд 31
Изучая различные отображения «золотого сечения» в жизни человека,
мы случайно нашли информацию, что соотношения длины и ширины
флага РСФСР (была в Советском Союзе такая республика) составляло 8:5. Заинтересовавшись, начали изучать информацию о флагах других государств.
Слайд 32
Проверили 63 флага.
В результате исследования выяснилось:
отношения сторон 2:1
— 19 флагов;
2,3:1,5 — 25 флагов;
2,5:1,5 — 9 флагов
(в том числе России);
другие размеры — 10 флагов.
Слайд 33
Вывод:
из 63 флагов государств 40 флагов имеют
соотношения длины и ширины в соответствии с «золотой пропорцией»,
видимо, интуитивная тяга к красивому присуща человеку во всех сферах его деятельности.
Слайд 35
Советский Союз
Осей симметрии нет, в 1991 году прекратил
свое существование
Слайд 37
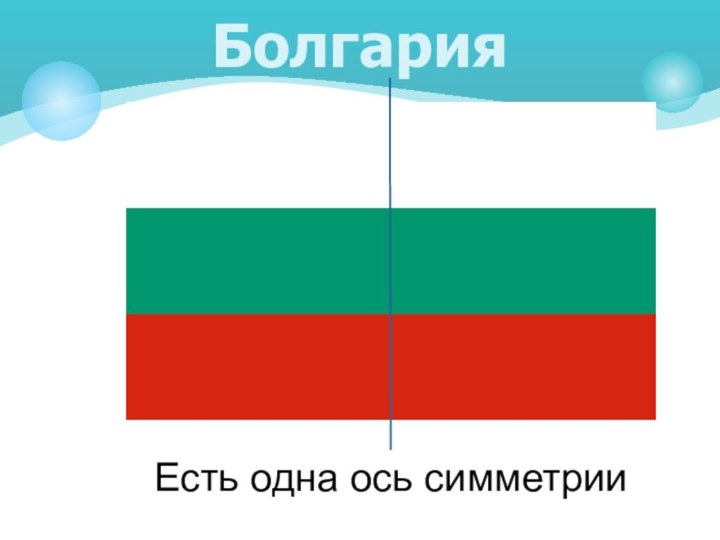
Болгария
Есть одна ось симметрии
Слайд 39
ГДР
Осей симметрии нет, 30 октября 1990 года перестала
существовать
Слайд 42
Чехословакия
Осей симметрии нет, в июне 1992 года Чехословакии
не стало
Слайд 43
Вывод:
при создании своего флага не пренебрегайте «золотым
сечением» и симметричностью.