- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Геометрия на сфере
Содержание
- 2. Сферой называется поверхность, которая состоит
- 3. Шаровой или сферической поверхностью называется геометрическое место
- 4. Рассмотрим окружность с центром О и радиусом
- 5. Через любые две точки на сфере, кроме
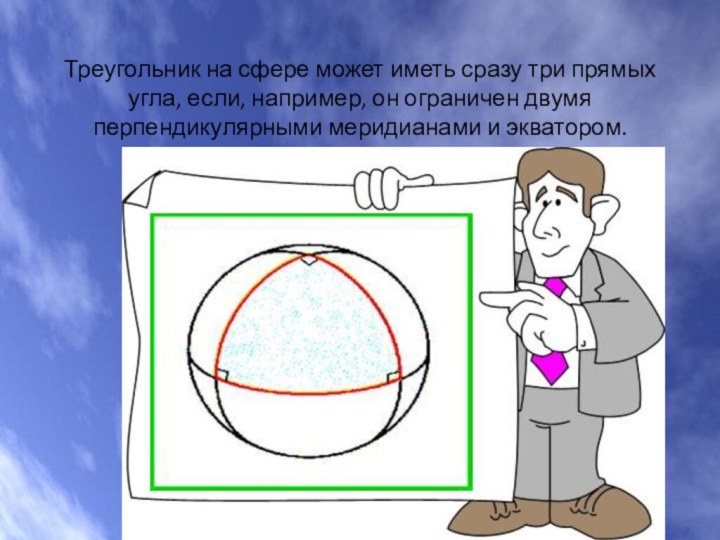
- 6. Треугольник на сфере может иметь сразу три
- 7. Длина сферического отрезка определяется через радианную меру
- 8. Сферическая окружность -множество точек сферы, равноудаленных от
- 9. При пересечении двух сферических прямых a и
- 10. Три больших окружности, пересекаясь попарно в двух
- 11. Множество точек, равноудаленных от концов отрезка будет
- 12. Доказательство сферической теоремы о медианах: Плоскости, содержащие
- 13. Треугольники, имеющие равные элементы и различную ориентацию, называются симметричными, таковы, например, треугольники АС`С и ВСС`
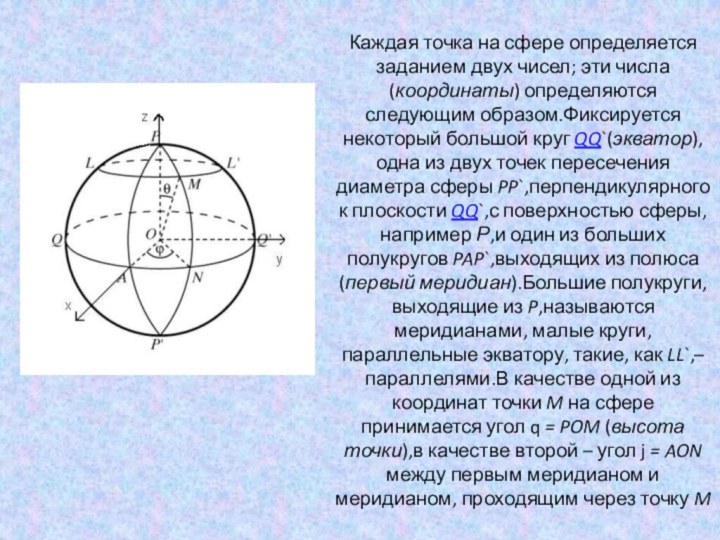
- 14. Каждая точка на сфере определяется заданием двух
- 15. Скачать презентацию
- 16. Похожие презентации
Сферой называется поверхность, которая состоит из всех точек пространства, находящихся на заданном расстоянии от данной точки. Эта точка называется центром, а заданное расстояние – радиусом сферы, или шара – тела, ограниченного сферой. Шар состоит













Слайд 3 Шаровой или сферической поверхностью называется геометрическое место точек
пространства, удаленных от данной точки О (центра) на заданное
расстояние R (радиус).Слайд 4 Рассмотрим окружность с центром О и радиусом R
, лежащую в плоскости λ. Будем вращать ее вокруг
диаметра АВ. Тогда каждая из точек окружности,, в свою очередь опишет при вращении окружность, имеющую своим центром точку М0—проекцию вращающейся точки М на ось вращения АВ. Шаровая поверхность может быть получена вращением окружности вокруг любого из ее диаметров.Слайд 5 Через любые две точки на сфере, кроме диаметрально
противоположных, можно провести единственный большой круг.Через диаметрально противоположные точки
проходит бесконечное количество больших кругов.Меньшая дуга AmB большого круга является кратчайшей из всех линий на сфере, соединяющих заданные точки. Такая линия называется геодезической.