- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Аркфункции
Содержание
- 2. «Функция, как правило, определяется для
- 3. sint = 0,5sint = 0,3При каких значениях t верно равенство?, t=?
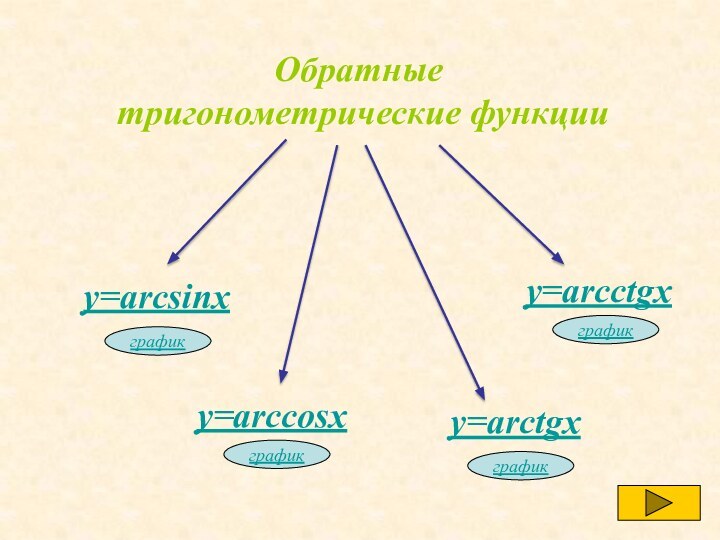
- 4. Обратные тригонометрические функции
- 5. Область определения функции — множество R всех
- 6. Область определения функции — множество R всех
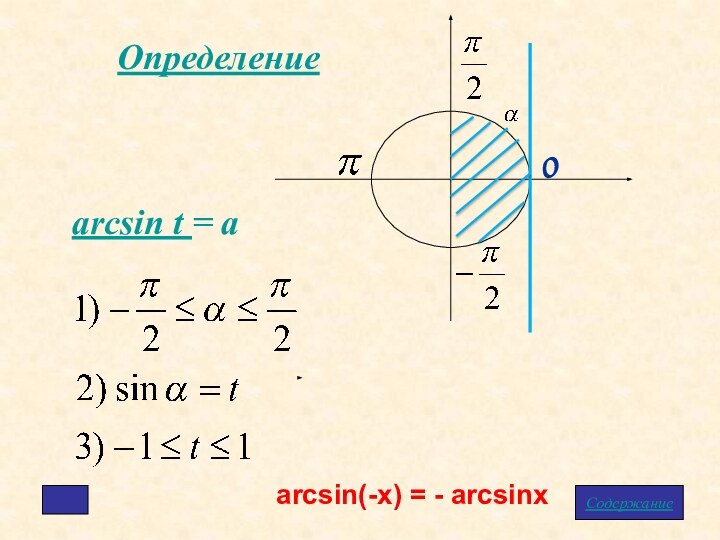
- 7. Определениеarcsin t = aarcsin(-x) = - arcsinxСодержание
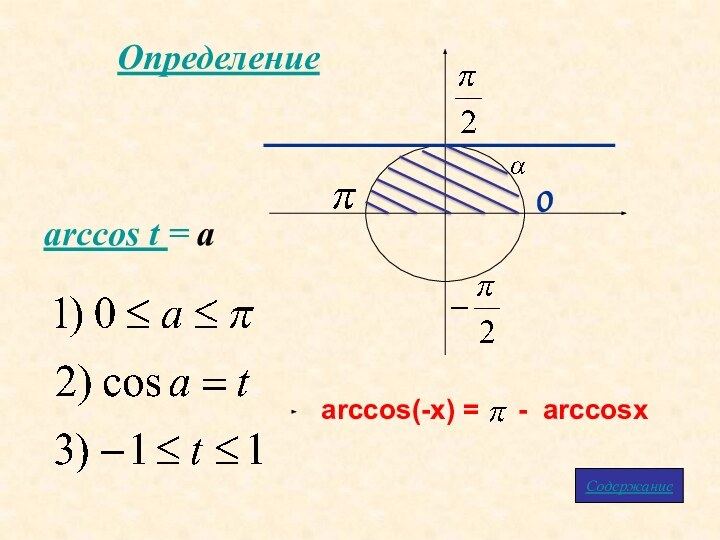
- 8. Определениеarccos t = aСодержаниеarccos(-x) = - arccosx
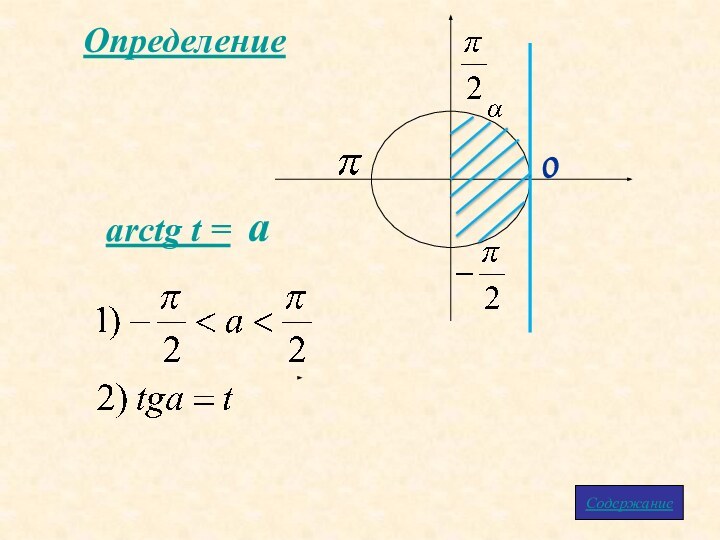
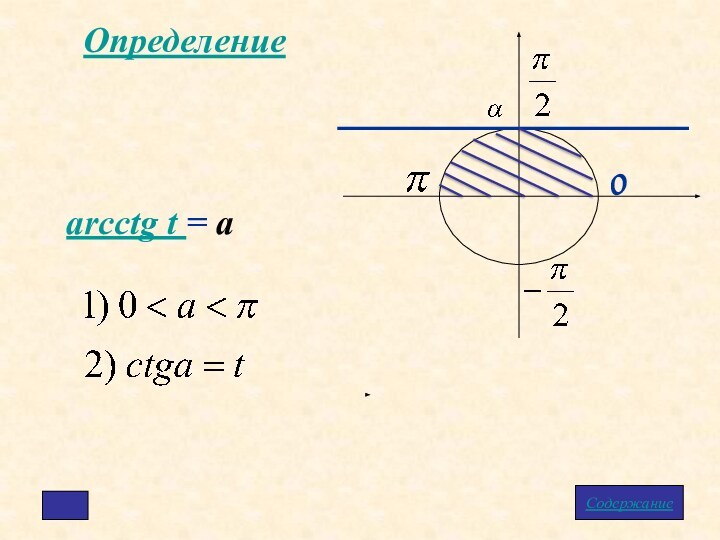
- 9. Определениеarctg t = aСодержание
- 10. Определениеarcctg t = aСодержание
- 11. у = arcsinxСодержаниех1)Область определения: отрезок [-1; 1];
- 12. у=arccos xСодержание1)Область определения: отрезок [-1; 1]; 2)Область
- 13. у=arctgxСодержание1)Область определения: R – множество действительных чисел
- 14. у=arcctgxСодержание1)Область определения: R - 2)Область значений:
- 15. Работаем устноСодержаниеarcsin(-x) = - arcsinxarccos(-x) = - arccosx
- 16. Работаем устноИмеет ли смысл выражение?Содержание
- 17. Работаем устноНайдите значения выражений:Содержание
- 18. Работаем устноСодержаниеarctg(-x) = - arctgxarcctg(-x) = - arcctgx
- 19. Свойства аркфункций
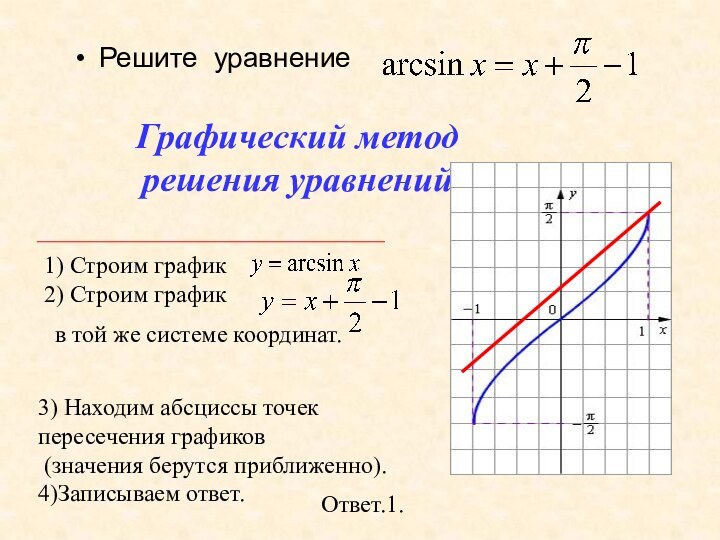
- 20. Решите уравнение Ответ.1.3) Находим абсциссы точек пересечения графиков (значения берутся приближенно).4)Записываем ответ.Графический метод решения уравнений
- 21. Функционально-графическийметод решения уравненийПример: решите равнение3) Уравнение f(x)=g(x)
- 22. Скачать презентацию
- 23. Похожие презентации
«Функция, как правило, определяется для тех значений аргумента, какие для данной задачи представляют реальноезначение»



![Аркфункции у = arcsinxСодержаниех1)Область определения: отрезок [-1; 1]; 2)Область значений: отрезок ; 3)Функция](/img/tmb/14/1362705/65cf5276401a4aecf7cb2a91741da5b9-720x.jpg)
![Аркфункции у=arccos xСодержание1)Область определения: отрезок [-1; 1]; 2)Область значений: отрезок 3)Функция у =](/img/tmb/14/1362705/800f06fad54737ec50f4c2037262752d-720x.jpg)







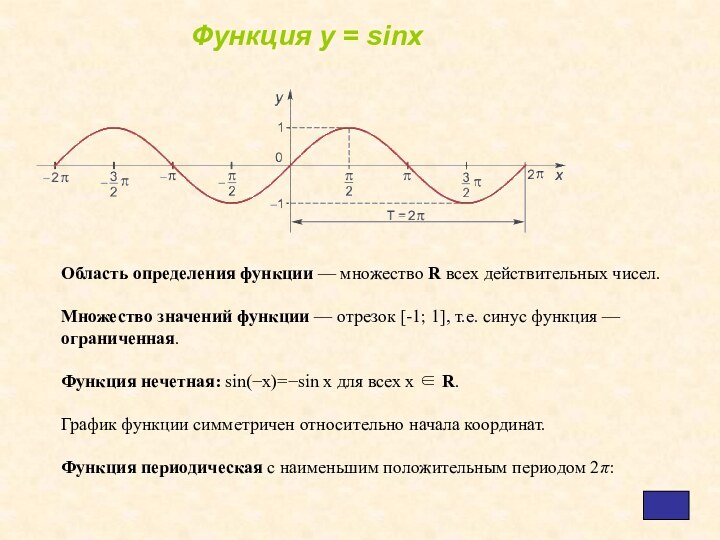
Слайд 5 Область определения функции — множество R всех действительных
чисел.
Множество значений функции — отрезок [-1; 1], т.е. синус
функция — ограниченная.Функция нечетная: sin(−x)=−sin x для всех х ∈ R.
График функции симметричен относительно начала координат.
Функция периодическая с наименьшим положительным периодом 2π:
Функция у = sinx
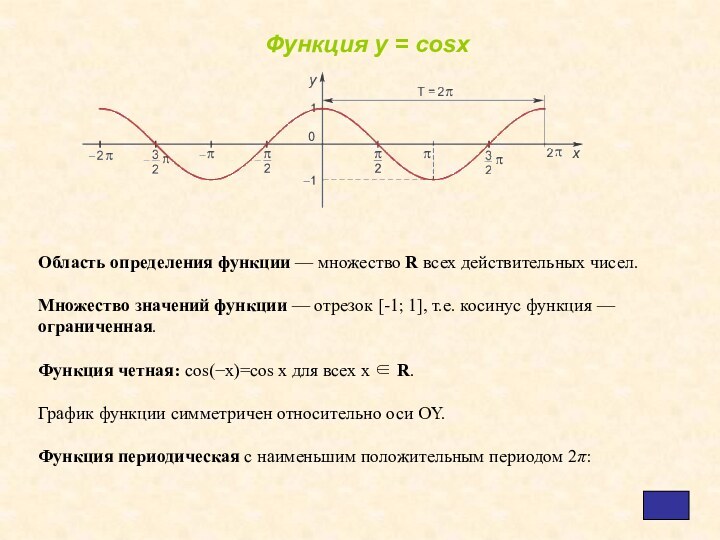
Слайд 6 Область определения функции — множество R всех действительных
чисел.
Множество значений функции — отрезок [-1; 1], т.е. косинус
функция — ограниченная.Функция четная: cos(−x)=cos x для всех х ∈ R.
График функции симметричен относительно оси OY.
Функция периодическая с наименьшим положительным периодом 2π:
Функция у = cosx
Слайд 11
у = arcsinx
Содержание
х
1)Область определения: отрезок [-1; 1];
2)Область
значений: отрезок
;
3)Функция у = arcsin x нечетная:
arcsin (-x) = - arcsin x;4)Функция у = arcsin x монотонно возрастающая;
Слайд 12
у=arccos x
Содержание
1)Область определения: отрезок [-1; 1];
2)Область значений:
отрезок
3)Функция у = arcсos x четная:
arcscos (-x)
= 4)Функция у = arcсosx монотонно убывающая;
Слайд 13
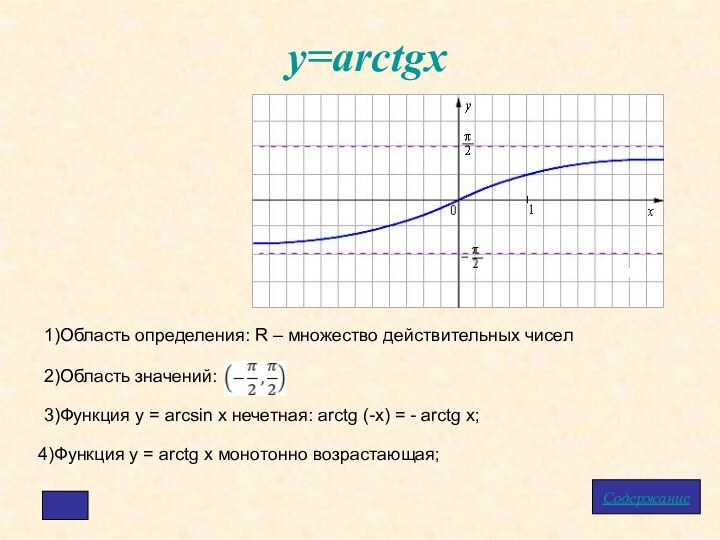
у=arctgx
Содержание
1)Область определения: R – множество действительных чисел
2)Область
значений:
3)Функция у = arcsin x нечетная: arctg
(-x) = - arctg x;4)Функция у = arctg x монотонно возрастающая;
Слайд 14
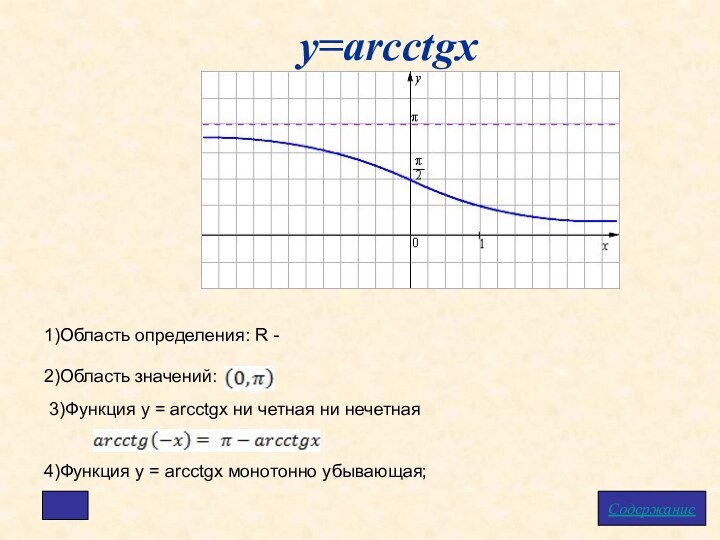
у=arcctgx
Содержание
1)Область определения: R -
2)Область значений:
4)Функция
у = arcсtgx монотонно убывающая;
3)Функция у = arcctgх
ни четная ни нечетная