Презентация на тему Элементы теории случайных процессов

с бесконечным числом свободы – атомарное строение вещества
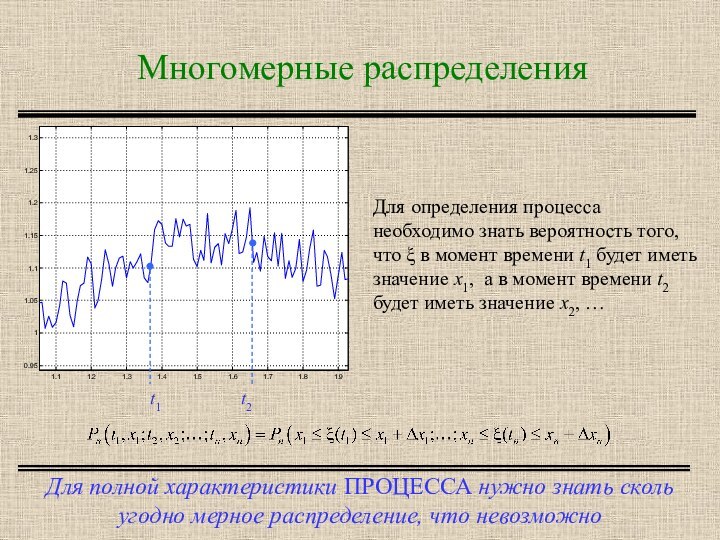
Световое поле

любого реального источника есть статистический сигнал – частичная когерентность
Фоны имеют сложную структуру случайно изменяющуюся по пространству и времени:
Волнений водной поверхности
Изменение прозрачности атмосферы
Природные фоны: лес, поля, горы – изменяются от места к месту по вероятностному закону
Шумы приемной аппаратуры

понятия теории вероятности – анализ азартных игр – задачи

с равновероятными исходами:

Вероятность орел – решка: P(о)= P(р)=1/2;
Грань игральной кости: P(г)=1/6;
Карта из колоды: P(к) =1/32;
В случае равновероятных исходов вероятность события A:

В такой системе возможны и более сложные ситуации – вероятность двух тузов в прикупе:

Общее определение вероятности по Laplace (Pierre-Simon, 1749–1827) для систем с равновероятными исходами:

зрения математической теории?
Hall A. On an experimental determinition of

π. – Messeng. Math., 1873, V2. P.113:

S(A)

Определим некоторую меру события, которая пропорцианальна площади:

Частотное определение вероятности Mises Richard (1883, Львов - 1953, Бостон):

физикой - частотой события
Задано пространство Ω элементарных событий (исходов)

ω: ω ∈Ω;
Событие A является множеством ω и подмножеством Ω – существует набор правил, по которым из элементов ω можно образовывать систему подмножеств – алгебра ;
Введена мера множества события A, удовлетворяющая правилам:
1 ≥ P(A)≥0: P(Ω)=1, P()=0

случайные величины
Случайная величина: функция ξ= ξ(ω), ω ∈Ω на

заданном вероятностном пространстве (Ω, ,P);
Случайная величина сама является случайным событием на вероятностном пространстве (X, ,Pξ) – непосредственно заданная случайная величина;
Алгебра  есть система интервалов на некотором сегменте X;
Pξ(B)= P(ξ ∈B);
Случайная величина может быть:

а ее распределение
Центральные моменты случайной величины:
- математическое ожидание (среднее)
Важнейшей

из которых является дисперсия:

является мостиком, соединяющим математическую теорию с физическим содержанием
Bernoulli Jacob

(1654 - 1705):
ξi – индикатор события A:

не будет характеризовать процесс
ξ(t)= ξ(t,ω), ω ∈Ω на заданном

вероятностном пространстве (Ω, ,P), t ∈T

t – одномерная величина (время) – случайный процесс;
t – многомерная величина (радиус-вектор r) – случайное поле
ξ= ξ(t,ω0) – реализация случайного процесса – осциллограмма тока или напряжения
ξ= ξ(t0,ω) – случайная величина, для которой можно ввести Mξ(t), Dξ(t) – функции параметра t