Слайд 2
Вопрос 1: Какая из следующих последовательностей является арифметической
прогрессией?
А. Последовательность натуральных степеней числа 3.
Б. Последовательность натуральных чисел,
кратных 7.
В. Последовательность квадратов натуральных чисел.
Г. Последовательность чисел, обратных натуральным.
Слайд 3
1. Какая из следующих последовательностей является арифметической прогрессией?
Правильно.
К
вопросу 2
Слайд 4
1. Какая из следующих последовательностей является арифметической прогрессией?
Не
верно.
В этой последовательности разница между соседними числами изменяется, а
должна быть постоянна.
Вернуться к вопросу 1
Слайд 5
Вопрос 2: Какая из следующих последовательностей не является
геометрической прогрессией?
А. Последовательность натуральных степеней числа 3.
Б. Последовательность, все
члены которой равны одному и тому же числу 3.
В. Последовательность, состоящая из чередования чисел 3 и -3.
Г. Последовательность, первый член которой равен 3, а все остальные члены - нули.
Слайд 6
2. Какая из следующих последовательностей не является геометрической
прогрессией?
Правильно.
К вопросу 3
Слайд 7
2. Какая из следующих последовательностей не является геометрической
прогрессией?
Не верно.
В этой последовательности отношение последующего члена к предыдущему
равно одному и тому же не равному нулю числу, а значит, - это геометрическая прогрессия.
Вернуться к вопросу 2
Слайд 8
Вопрос 3: Какое число не является членом арифметической
прогрессии 6, 12, 18, …?
А. 60
Г. 72
Б. 63
В. 66
Слайд 9
Правильно.
К вопросу 4
3. Какое число не является членом
арифметической прогрессии 6, 12, 18, …?
Слайд 10
Не верно.
Вспомни, что аn = a1 + d(n-1),
где a1 = 6, d = 12 – 6
= 6, откуда
аn = 6 + 6(n-1) = 6 + 6n – 6 = 6n, то есть каждый из членов прогрессии нацело делится на число 6.
Вернуться к вопросу 3
3. Какое число не является членом арифметической прогрессии 6, 12,18, …?
Слайд 11
Вопрос 4: Какое число является членом геометрической прогрессии
6, 12, 24, …?
А. 192
Г. 60
Б. 100
В. 84
Слайд 12
Правильно.
К вопросу 5
4. Какое число является членом геометрической
прогрессии 6, 12, 24, …?
Слайд 13
Не верно.
Вспомни, что q = bn+1 : bn
,
найди q = 12 : 6 = 2
и выпиши еще несколько членов данной прогрессии!
Вернуться к вопросу 4
4. Какое число является членом геометрической прогрессии 6, 12, 24, …?
Слайд 14
Вопрос 5: известны несколько последовательных Членов арифметической прогрессии:
…-12; x; 14; 27… Найдите число x.
А. -1
Б. 0
В.
1
Г. 2
Слайд 15
Не верно!
Определи разность прогрессии или вспомни ее характеристическое
свойство!
Вернуться к вопросу №5
5. известны несколько последовательных Членов арифметической
прогрессии:
…-12; x; 14; 27… Найдите число x.
Слайд 16
Правильно! Молодец!
Переходи к вопросу 6
5. известны несколько последовательных
Членов арифметической прогрессии:
…-12; x; 14; 27… Найдите число
x.
Слайд 17
Вопрос 6: известны несколько последовательных членов геометрической прогрессии:
…2; y; 8; -16;… Найдите число Y.
А. – 4
Б. – 5 В. 4 Г. 5
Слайд 18
Вернись назад
Не верно!
Определи знаменатель прогрессии или вспомни ее
характеристическое свойство!
6. известны несколько последовательных членов геометрической прогрессии:
…2;
y; 8; -16;… Найдите число Y.
Слайд 19
Молодец! Правильно!!!
Перейти к вопросу 7
6. известны несколько последовательных
членов геометрической прогрессии:
…2; y; 8; -16;… Найдите число
Y.
Слайд 20
Вопрос 7: Найди сумму первых пяти членов геометрической
прогрессии, если известно, что ее первый член равен 48,
а знаменатель равен -0,5.
А. – 93 Б. – 33 В. 33 Г. 93
Слайд 21
Вернись назад
Не верно!
Выпиши первые четыре члена прогрессии и
сложи их!
7. Найди сумму первых пяти членов геометрической прогрессии,
если известно, что ее первый член равен 3, а знаменатель равен -2.
Слайд 22
Молодец! Правильно!!!
Перейти к вопросу 8
7. Найди сумму первых
пяти членов геометрической прогрессии, если известно, что ее первый
член равен 3, а знаменатель равен -2.
Слайд 23
Вопрос 8: Найди сумму первых восьми членов арифметической
прогрессии, если известно, что ее первый член равен 4,
а разность равна -2.
А. – 18
Б. – 20
В. – 24
Г. – 32
Слайд 24
Ошибка!
Выпиши первые восемь членов прогрессии, а затем сложи
их.
Вернуться к вопросу 8
8. Найди сумму первых восьми членов
арифметической прогрессии, если известно, что ее первый член равен -4, а разность равна 2.
Слайд 25
Молодец! Правильно!!!
Перейти к задаче Карла Гаусса
8. Найди
сумму первых восьми членов арифметической прогрессии, если известно, что
ее первый член равен -4, а разность равна 2.
Слайд 26
Задача гаусса
К.Ф.Гаусс
Чему равна сумма первых ста натуральных чисел
?
Ответ: 5050
Слайд 27
S100= 1 + 2 + 3 +…+ 98
+ 99 + 100
1; 2; 3; 4; 5;...;
100
a1 = 1, a100 = 100, d=1; S100 = ?
S100= 100 + 99 + 98 +… + 3 + 2 +1
2S100 = 101 + 101 +…+ 101 + 101
= 5050
S100 = 10100:2
100 раз
2S100 = 10100
Слайд 28
(1)
Дано: (an) = a1; a2; a3;…; an- арифметическая
прогрессия.
Sn= a1 + a2
+ a3 +…+ an-2 + an-1+ an
Sn= an +an-1 + an-2 +…+ a3 + a2 + a1
2Sn=
Найти: Sn
Решение:
2Sn= (a1+ an)n
n раз
Слайд 29
Формула суммы членов конечной арифметической прогрессии
Слайд 30
Практическое применение формулы суммы первых n первых членов
арифметической прогрессии
(an) – арифм. прогрессия
a1 = 1, d=1, n = 100
S100 = ?
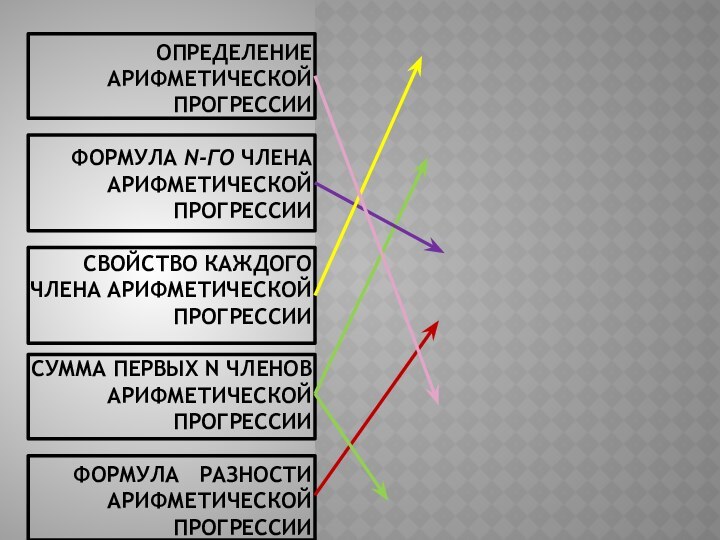
арифметической
прогрессии
Формула n-го члена
арифметической
прогрессии
Свойство каждого
члена арифметической
прогрессии
Сумма первых n членов
арифметической
прогрессии
Формула разности
арифметической
прогрессии
Слайд 32
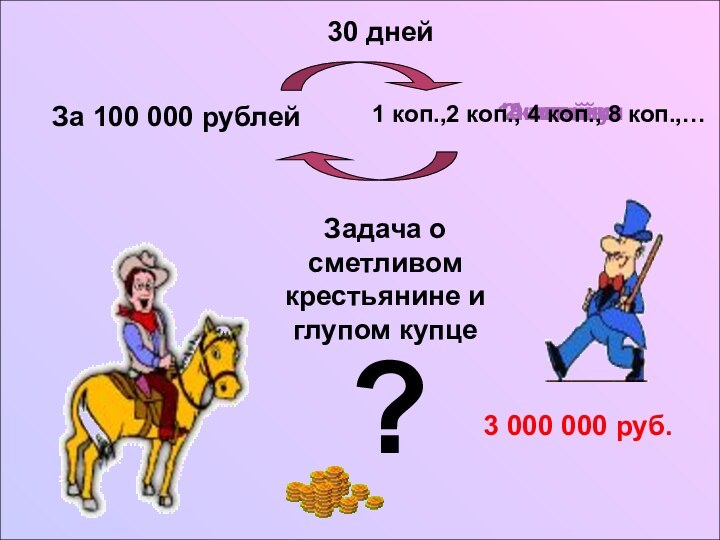
За 100 000 рублей
1 копейку
2 копейки
4 копейки
8 копеек
3 000 000 руб.
1 коп.,2 коп., 4 коп.,
8 коп.,…
30 дней
Задача о сметливом крестьянине и глупом купце
Слайд 33
S30=1 + 2 + 4 + 8 +16
+...+ 229
1; 2; 4; 8; 16;...; 229
· 2
2S30=2
+ 4 + 8 +16 +32+...+229 +230
2S30- S30 =
= 1 073 741 823 (коп) =
= 10 737 418,23 (руб)
S30 = 230 -1
b1 = 1, b30 = 229, q=2; S30 = ?
2S30- S30 = 230 -1
S30 =
Слайд 34
(3)
Дано: (bn)= b1; b2; b3;…; bn- геометрическая
прогрессия.
Sn= b1+ b2+ b3+…+ bn
qSn=b1q+b2q+b3q+…+bn-1q+bnq
·
q
qSn- Sn= bnq- b1
Sn·(q-1) = bnq- b1
Найти: Sn
Решение:
Слайд 37
Практическое применение формулы суммы первых n первых членов
геометрической прогрессии
(bn) – геом. прогрессия
b1 = 1, q=2, n = 30
S30 = ?
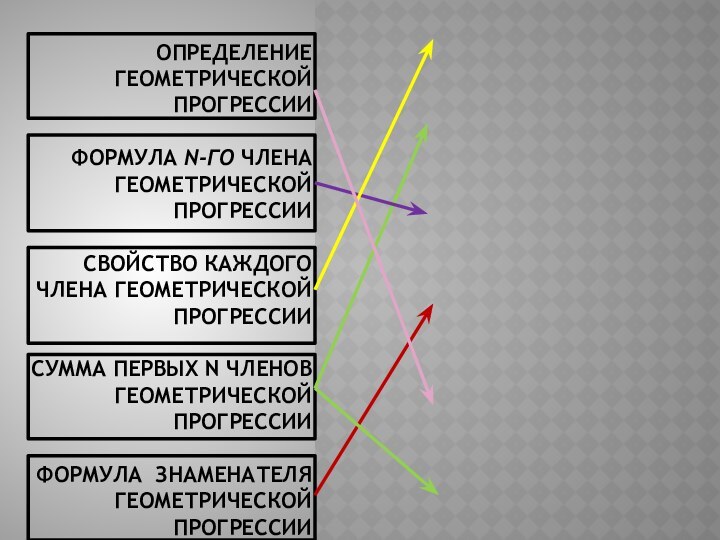
геометрической
прогрессии
Формула n-го члена
геометрической
прогрессии
Свойство каждого
члена геометрической
прогрессии
Сумма первых n членов
геометрической
прогрессии
Формула знаменателя
геометрической
прогрессии
Слайд 39
Домашнее задание
1) читать п.п. 26 и 28 учебника;
2)
выполнить творческую работу «Шпаргалка с формулами для решения задач
на прогрессии»;
3) записать в тетради доказательство всех выведенных на уроке формул.