Лейбницем, который основываясь на результатах Ферма и некоторых других
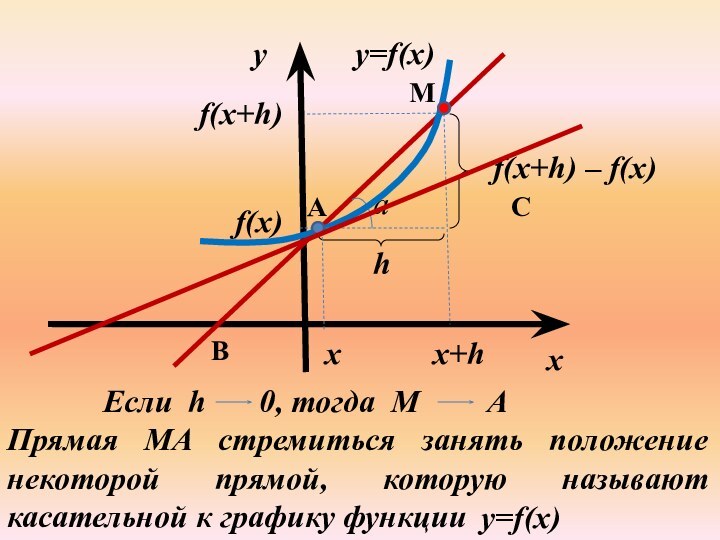
выводах, значительно полнее своих предшественников решил задачу о построении касательной к кривой в некоторой точке.
1646г – 1716г
Готфрид Вильгельм фон Лейбниц
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть







1646г – 1716г
Готфрид Вильгельм фон Лейбниц
a
x
o
a
y
y=f(x)
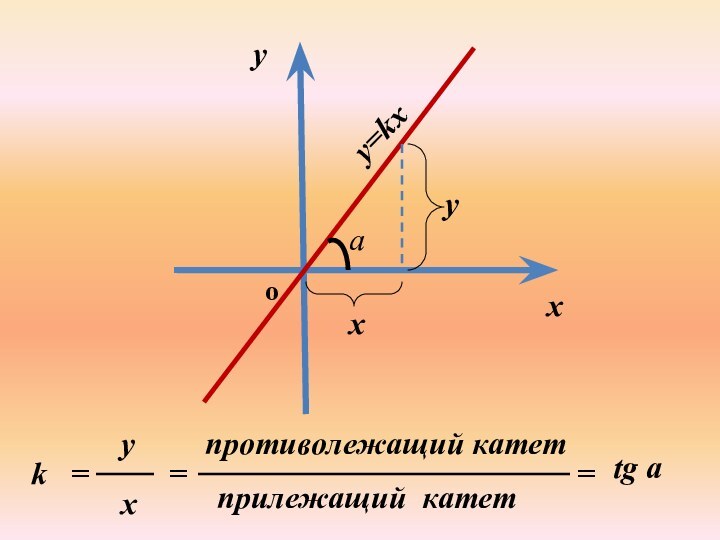
tg a
f ' (x)
=
h
0
Значение производной в точке равно
угловому коэффициенту касательной к графику функции в этой точке
Если угол наклона прямой, то тангенс не существует, а значит, производная не существует.
Т.к. касательная проходит через точку с координатами
(х0; f(x0)) , подставим ее координаты в уравнение (2) и найдем b
(1)
(2)
f(x0)=f' (x0 )x0+ b
b =f(x0) – f' (x0 )x0
Подставьте в уравнение (2) значение b и сделав соответствующие преобразования получите:
у = f(x0) + f '(x0)(х – х0)