Презентация на тему Использование метода ЛАЧХ для синтеза регуляторов манипулятора с гибким стержнем

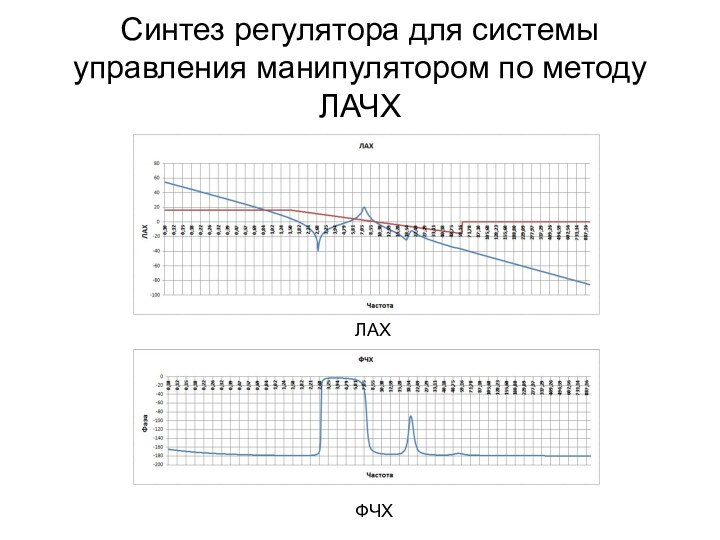
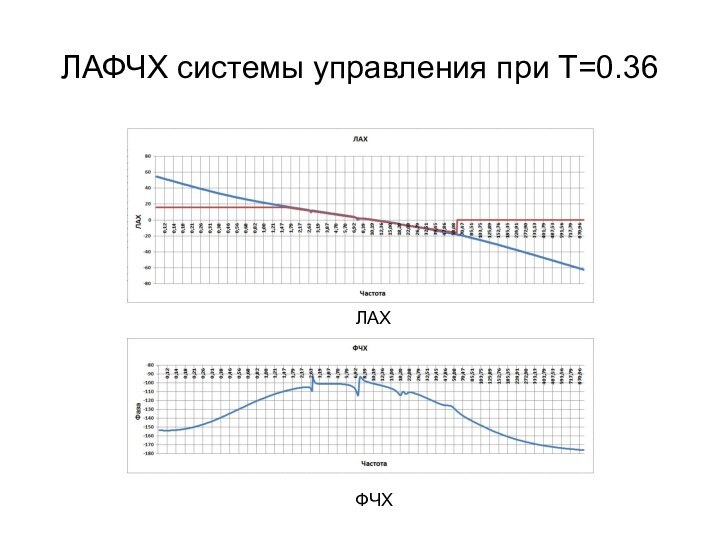
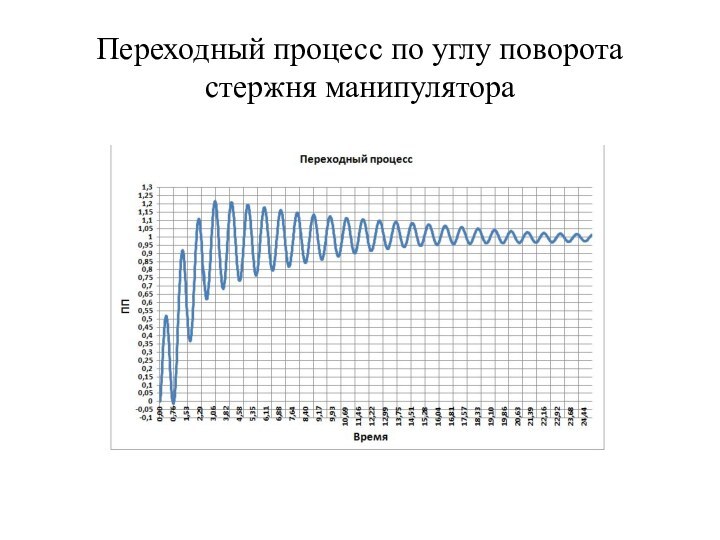
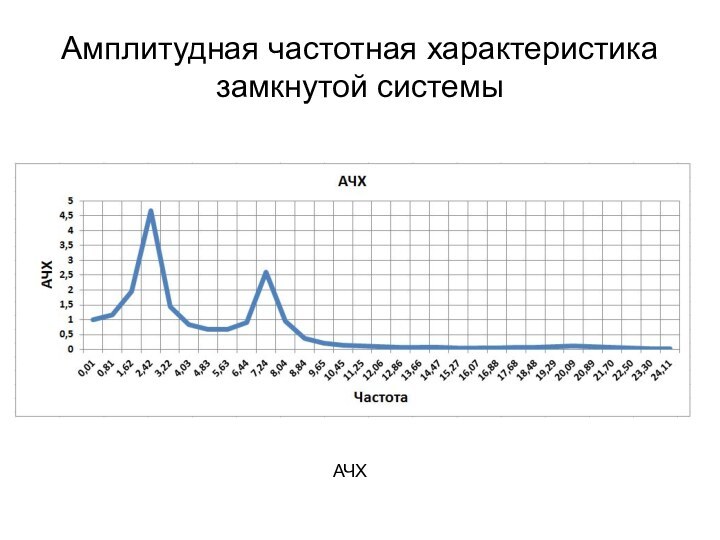
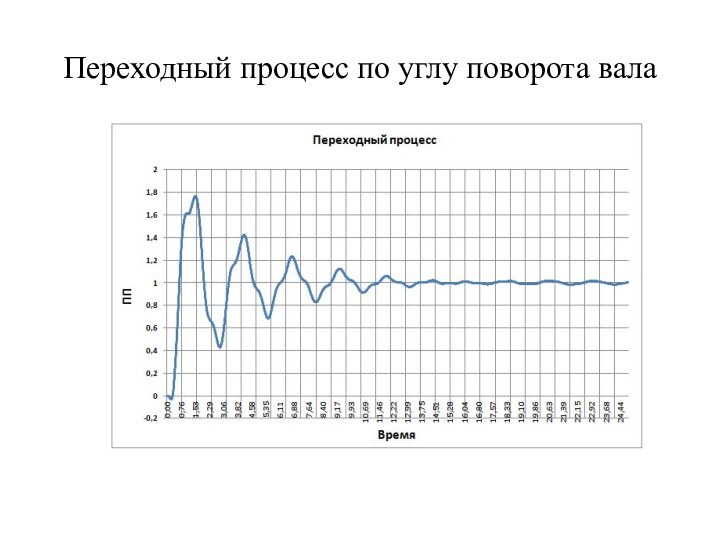
вязкоупругого стержня – сложная комбинированная система, состоящая из сосредоточенных

и распределенных элементов. Для синтеза регулятора таких систем используются методы параметрической оптимизации, которые сложны и не наглядны.
Является актуальным использовать для синтеза регулятора таких систем хорошо известный инженерам и наглядный метод логарифмических амплитудных и фазовых частотных характеристик.

метода логарифмических амплитудно-частотных характеристик для синтеза регулятора системы управления

манипулятором с упругим стержнем.

гибких стержнях характерные процессы определяются такими параметрами стержней и

их материала:
E – модуль Юнга упругости материала;
J – момент инерции поперечного сечения стержня;
s – длина стержня;
ρ – плотность материала стержня.
Их этих параметров можно составить комбинацию имеющую размерность времени

Эта комбинация представляет собой характерное время протекающих в стержнях процессов

длины можно ввести безразмерные переменные

y1 =y1*/ δ ,

y1- безразмерное упругое перемещение конца стержня;
y =y*/ δ, y – безразмерный прогиб стержня;
z=z*/ s, z – безразмерная координата поперечного сечения стержня.

движения абсолютно твердых вала и исполнительного органа.




Дифференциальное уравнение

с частными производными, моделирующее процессы изгиба стержня.

Граничные условия.

Начальные условия.

Уравнения связи абсолютно твердых вала и исполнительного органа через гибкий стержень.

схема системы стабилизации манипулятора с регулятором самого общего вида
передаточная

функция замкнутой системы управления

передаточная функция разомкнутой системы управления

ЛАЧХ
ЛАХ
ФЧХ

РАБОТЕ:
1. Разработаны размерная и безразмерная математические модели системы управления

манипулятора с рабочим инструментом в виде вязкоупругого стержня.
2. Сформирована структурная схема системы управления плоским движением манипулятора с вязкоупругим стержнем. Получены передаточные функции разомкнутой и замкнутой систем управления манипулятором.
3. Методом логарифмических амплитудных и фазовых частотных характеристик получены корректирующие устройства для системы управления плоским движением манипулятора с вязкоупругим стержнем, для разных значений частотных показателей качества управления.
4. Показано, что для системы управления манипулятора с рабочим инструментом в виде вязкоупругого стержня для получения приемлемых показателей переходных процессов требуются более высокие частотные показатели качеств по сравнению с системами с сосредоточенными параметрами.