Презентация на тему Линейное уравнение с двумя переменными и его график

дать понятие об уравнении с двумя переменными, их решении

и графике уравнения

материала:
Алгоритм нахождения координат точки.
Алгоритм построения точки в системе координат.
Укажите

координаты точек В и С, симметричных точке А(-5; 2) относительно оси х и оси у соответственно.

1.
Первое число (обозначим его х) больше квадрата второго числа

(обозначим его у) на 3.
х – у² = 4
Выполняется ли это равенство при х=20 и у = 4?
А при х = 15 и у = 2?

х – у²

= 4
Подобные равенства с двумя переменными называют уравнениями с двумя переменными. Пару чисел х = 20 и у = 4 называют решением уравнения.
Решение можно записать также в виде (20; 4).

содержащее две переменные, называется уравнением с двумя переменными.
Если

в уравнении неизвестные входят только в первой степени, то такое уравнение называют линейным уравнением с двумя переменными.
Линейное уравнение имеет вид ах + bу + с=0 (где х и у – переменные, а, b, с – некоторые числа.

линейными являются уравнения
3х – 4у + 1 =

0, 5х + 7у = 0 и т. д.

Решением уравнения с двумя неизвестными называется пара значений переменных (х; у), при подстановке которых уравнение становится верным числовым равенством.

с двумя переменными, имеющие одни и те же решения,

называют равносильными.
Уравнения с двумя переменными, не имеющие решений, также считаю равносильными.

с двумя переменными обладают такими же свойствами, как и

уравнения с одной переменной.
Если в уравнении перенести любой член из одной части в другую, изменив его знак, то получится уравнение, равносильное данному.
Если обе части уравнения умножить или разделить на одно и то же (не равное нулю), то получится уравнение, равносильное данному.

2

а) Уравнения 3х² + 4у³ = 5 и 3х²

= 5 – 4у³ равносильны, т.к. член 4у³ перенесён (с изменением знака) из левой части в правую.
б) Уравнения и 3х² + 4у³ = 5 равносильны, т.к. обе части первого уравнения умножили на число 12 (не равное нулю) и получили второе.

3
Рассмотрим линейное уравнение 2х + 3у – 6 =

0 и построим его график.
Подберём несколько решений данного уравнения.
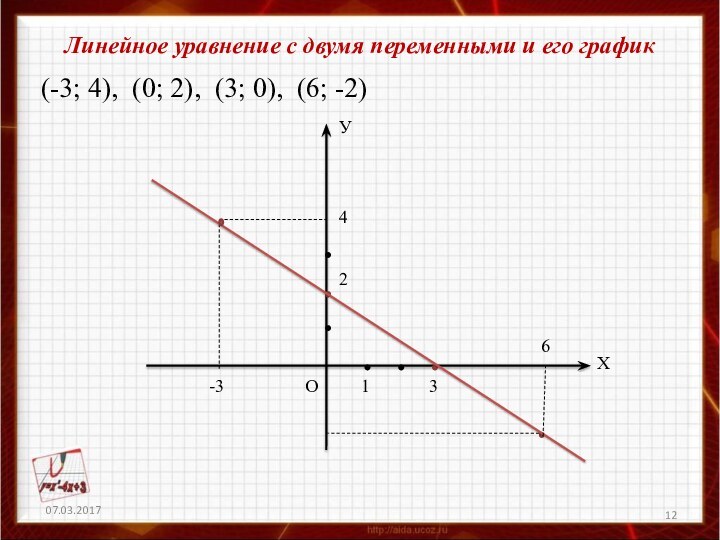
(-3; 4), (0; 2), (3; 0), (6; -2)
Построим эти точки на координатной плоскости.

4), (0; 2), (3; 0), (6; -2)

У
Х
6
2
4
О
1
-3
3

по примеру
1 Для построения графика уравнения 2х + 3у

– 6 = 0
можно было не подбирать, а находить такие
решения.
2х + 3у – 6 = 0
3у = – 2х + 6

по примеру
2. Графиком линейного уравнения ах + bу +

с = 0
является прямая линия.
3. Для построения прямой достаточно двух точек.
4. В качестве этих точек удобно выбирать точки пересечения графика функции с осями координат.

на уроке:
№ 7.1(а); 7.2(б); 7.4(г); 7.7(а); 7.11(б); 7.14(г); 7.17(а,

г); 7.25(а); 7.28(б); 7.29(б); 7.30; 7.39(а, б);

задание:
№ 7.1(б); 7.2(а); 7.4(в); 7.7(б); 7.11(г); 7.14(б); 7.17(б, в);

7.25(б); 7.28(а); 7.29(а); 7.31; 7.39(в, г);