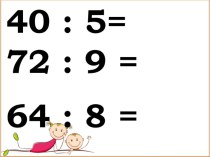- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Математические расчеты для оптимизации игры в преферанс
Содержание
- 2. Pn= 1 * 2 * 3 * ... * n = n!
- 3. Число способов с помощью которых можно выбрать
- 4. Число различных вариантов равно сочетания Cmn = Amn/Pm= n!/(m!*(n-m)! Cn-mn= n!/((n-m)!*(n-n+m)! = n!/(m!*(n-m)! = Cmn
- 5. Общее число раскладов рук вистующих C1020 = 20!/(10!*(20-10)!) = 11*12*13*14*15*16*17*18*19*20 / (1*2*3*4*5*6*7*8*9*10) = 184756.
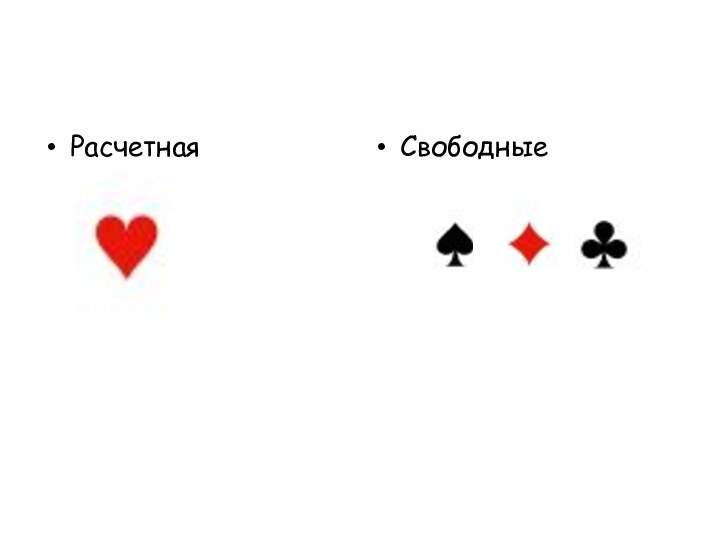
- 6. РасчетнаяСвободные
- 7. Играющий [Вистуюшие1вистующий
- 8. Вероятность распределения четырехкартной масти 4‑0.
- 9. В сумме получает 8008 + 8008 =
- 10. Играющий [Вистуюшие1вистующий
- 11. Вероятность распределения четырехкартной масти 3‑1
- 12. В сумме получает 45760 + 45760 =
- 13. Играющий [Вистуюшие1вистующий
- 14. Вероятность распределения четырехкартной масти 2‑2
- 15. Вероятность расклада 2-2, таким образом, равна:P2-2 = 77220/184756 = 41%.
- 16. Математическое ожидание(2*9+3*50+4*41)/100=332/100=3,32
- 17. Распределение у вистующих двух мастей длинной
- 18. P4-13-0 = (1100+1100)/184756 = 1,19%; P4-12-1 =
- 19. P3-23-0 = (4950+4950)/184756 = 5,36%; P3-22-1 =
- 20. Особая карта. (В данной ситуации)
- 21. Комбинация [Т К В]
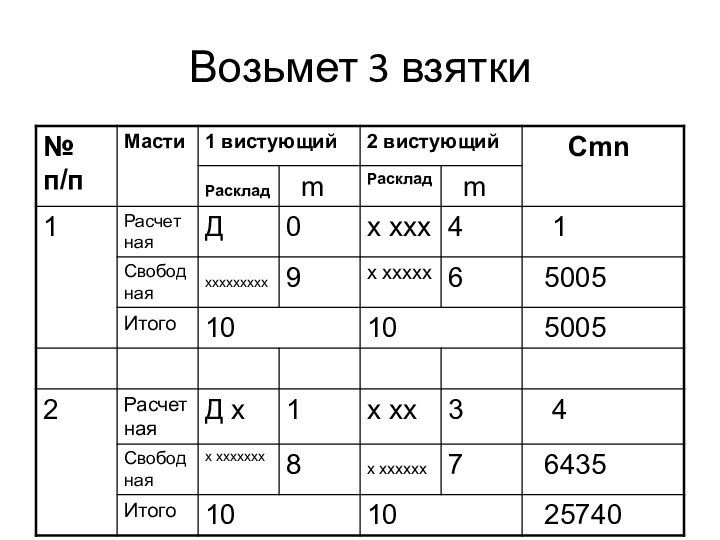
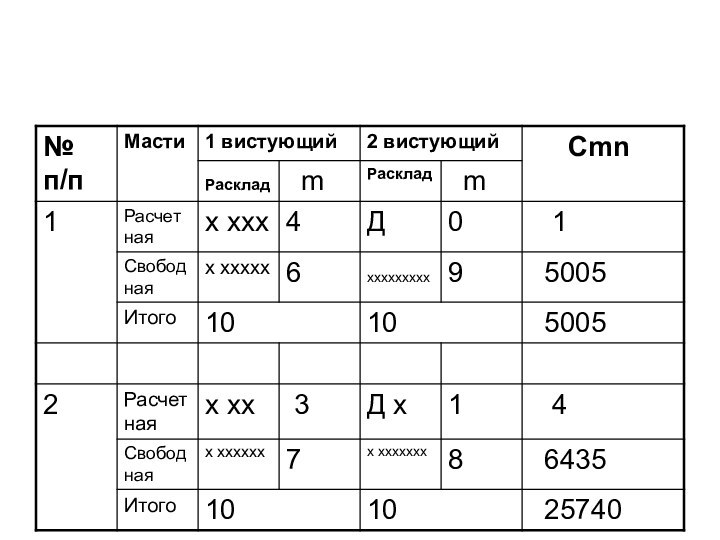
- 22. Возьмет 3 взятки
- 24. Вероятность взятия дополнительной третьей взятки Всего: 5005+25740+5005+25740=61590P3[ТКВ] = 61590/184756 = 33,28%.
- 25. Скачать презентацию
- 26. Похожие презентации
Pn= 1 * 2 * 3 * ... * n = n!

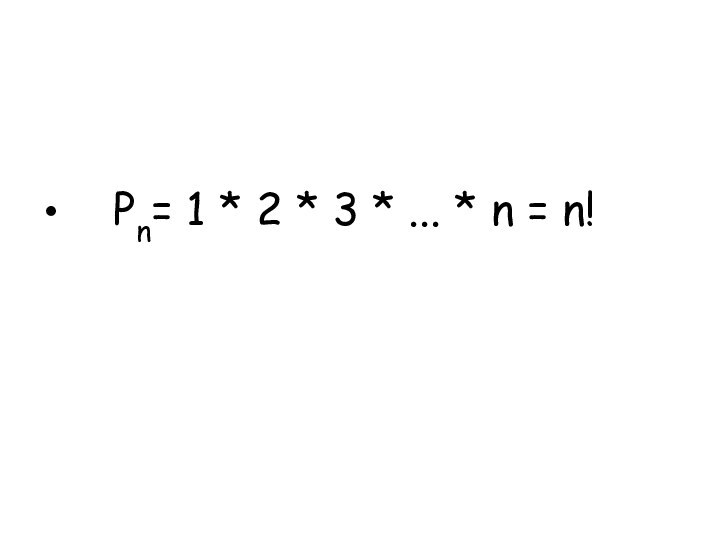



![Математические расчеты для оптимизации игры в преферанс Играющий [Вистуюшие1вистующий 2вистующий [Д;В;10;8]](/img/tmb/11/1061537/a9b25bab2226398a9e30cb43dd3d8af0-720x.jpg)


![Математические расчеты для оптимизации игры в преферанс Играющий [Вистуюшие1вистующий 2вистующий [Д;В;10;8]](/img/tmb/11/1061537/d889e634abc8ee148b8efd0ba30940cf-720x.jpg)


![Математические расчеты для оптимизации игры в преферанс Играющий [Вистуюшие1вистующий 2вистующий [Д;В;10;8]](/img/tmb/11/1061537/da0b8aeb2de6d5c55772487b7a751589-720x.jpg)







![Математические расчеты для оптимизации игры в преферанс Комбинация [Т К В]](/img/tmb/11/1061537/1c3147b94ff8a7cc3c6f6abf5c7b1390-720x.jpg)
![Математические расчеты для оптимизации игры в преферанс Вероятность взятия дополнительной третьей взятки Всего: 5005+25740+5005+25740=61590P3[ТКВ] = 61590/184756 = 33,28%.](/img/tmb/11/1061537/c0f5b61d97720f70feed440a74bee04c-720x.jpg)

Слайд 3 Число способов с помощью которых можно выбрать группу
m, из n.
Amn = (n-m+1) * (n-m+2) *
... * n = n!/(n-m)!число способов с помощью которых можно выбрать группу m, из n.