и встали в очередь. Сколькими способами они могут расположиться
друг за другом? Выпишите эти способы.Обозначим:
Андрея- буквой А, а Бориса- Б.
Друг за другом они могут расположиться только двумя способами
АБ или БА.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть




















Обозначим:
Андрея- буквой А, а Бориса- Б.
Друг за другом они могут расположиться только двумя способами
АБ или БА.
Пункт 26 №2.
Ответ: всего получилось 9 элементарных событий.
Первый способ решения
Обозначим :
Андрея- буквой А,
Бориса- буквой Б,
Владимира- буквой В.
Следовательно, получается :
АБВ,АВБ, БАВ,БВА,ВАБ,ВБА.
Итого 6 способов.
Второй способ решения
Первым может стоять
любой из 3 мальчиков,
следующим любой из 2, оставшийся мальчик будет последним( 1 вариант)
Получим 3!=1·2∙3=6
Итого 6 способов.
cdab не является элементарным событием,
так как все бракованные детали обнаружили
после второго извлечения.
а) Является ли сdаЬ элементарным событием в этом опыте?
б) Какими буквами может заканчиваться запись элементарного события?
запись элементарного события может заканчиваться буквами c или d.
г) Сколько различных элементарных событий записывается тремя буквами?
в) Выпишите все элементарные события этого опыта.
Мы знаем, что запись элементарного события должна заканчиваться буквами c или d. Сначала запишем все события (элементарные и неэлементарные), а потом вычеркнем те, которые заканчиваются на буквы a и b.
Abcd badc cabd dabc
Abdc bacd cadb dacb
Adbс bdca cbad dbac
Adсb bdac cbda dbca
Acbd bcad cdab dcab
Acdb bcda cdba dcba
Посчитаем оставшиеся события : abcd, bdac, cabd, dabc, abdc, bacd, adbc, cbad, dbac, bdac, acbd,bcad, acdb.
г) Сколько различных элементарных событий записывается тремя буквами?
Сначала составим все события:
Вычеркнем неэлементарные:
abc abd acd bcd
acb adb adc bdc
bac bad cad cbd
bca bda cda cdb
cab dba dac dbc
cba dab dca dcb
Остались события: acd, adc, cad, dac, bcd, bdc, cbd, dbc.
Всего: 8
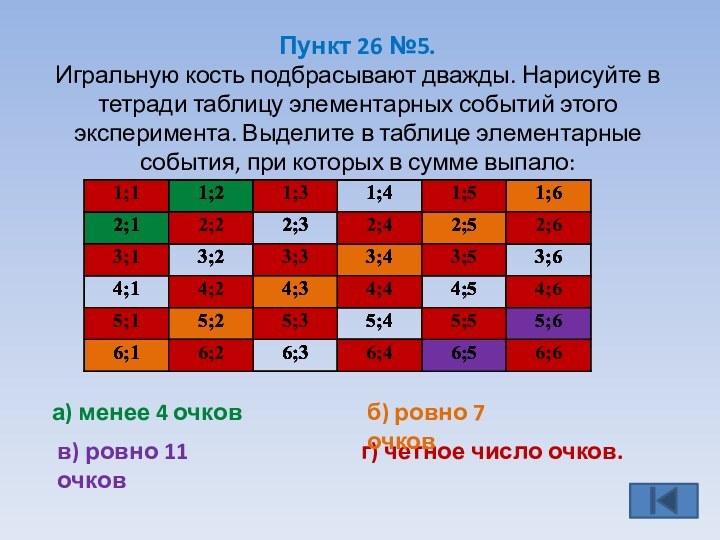
г) четное число очков.
а) менее 4 очков
б) ровно 7 очков
в) ровно 11 очков
Пункт 26 №6. При подбрасывании монеты будем обозначать буквой О выпадение орла и буквой Р выпадение решки.
Опыт 1:
Элементарные события: ОО, РР,ОР, РО.
Опыт 2:
Элементарные события:
ООО,ООР, ОРО, ОРР, РРР, РОО, РОР, РРО.
Опыт 3:
В 2 раза.
Пункт 26 №6. При подбрасывании монеты будем обозначать буквой О выпадение орла и буквой Р выпадение решки.
Опыт 5*:
1024, т.к. при подбрасывании выпадает 1024 различных
комбинаций. Это можно узнать, возведя 2 в 10 степень.
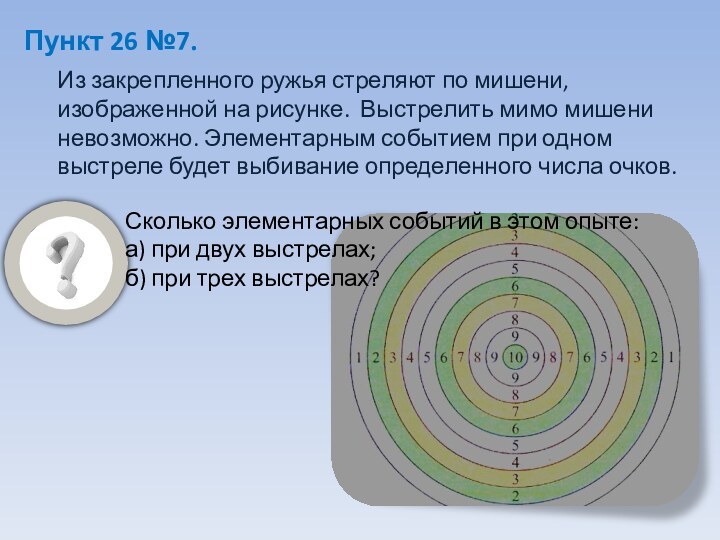
Сколько элементарных событий в этом опыте:
а) при двух выстрелах;
б) при трех выстрелах?
Б) При трёх выстрелах, элементарных событий 10х10х10=1000, к каждому из десяти возможных элементарных событий при первом выстреле может присоединиться любое из десяти событий при втором выстреле и может присоединиться любое из десяти событий при третьем выстреле.
а) При двух выстрелах 100 элементарных событий
б) При трёх выстрелах 1000 элементарных событий.
а) Запишите все возможные элементарные события.
б) Запишите все элементарные события, при которых встречу выигрывает команда «Физик».
Элементарные события :
ММ,ФФ,МФМ, ФММ, ФМФ,МФФ
ФФ,ФМФ,МФФ
Две буквы Ф, одна из которых является последней
в) Предположим, что во встрече победила команда «Математик». Какой буквой оканчивается запись соответствующих элементарных событий?
г) Какое наибольшее количество матчей может состояться?
Запись оканчивается буквой М
3 матча
Если после первых двух игр победитель не определился,
то победитель третьего матча станет победителем встречи
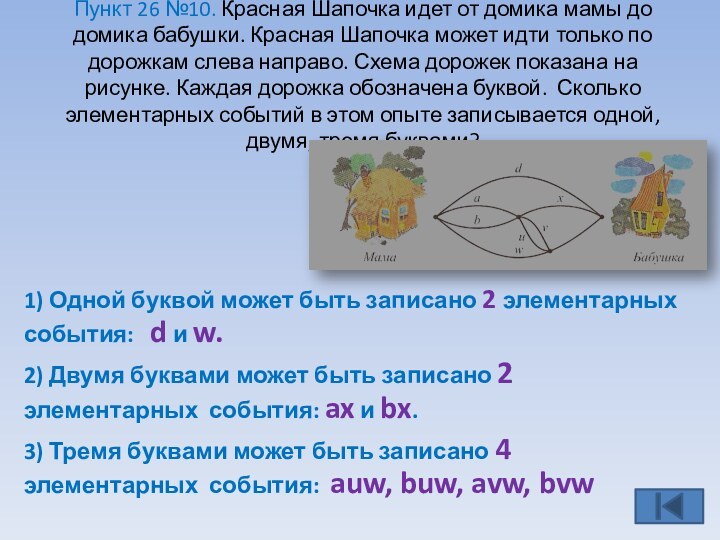
1) Одной буквой может быть записано 2 элементарных события: d и w.
2) Двумя буквами может быть записано 2 элементарных события: ax и bx.
3) Тремя буквами может быть записано 4 элементарных события: auw, buw, avw, bvw
а) 0, т.к это невозможное событие.
б)1, при выпадении 111
в)3, при выпадении 112,121,211
а) «выпало более17 очков»
элементарное событие: 6+6+6
Всего 1 элементарное событие.
б) «выпало более16 очков»
элементарные события: 5+6+6, 6+6+5, 6+5+6, 6+6+6.
Всего 4 элементарных события.
в) «выпало более15 очков».
элементарные события:
4+6+6, 6+6+4, 6+4+6,
5+5+6, 5+6+5, 6+5+5,
5+6+6, 6+5+6, 6+6+5,
6+6+6. Всего 10 элементарных событий.