Слайд 2
Математика –
не скучный и «сухой»
предмет!
Урок математики может и должен быть занимателен и
интересен. Сейчас и учебники становятся более красочно иллюстрированными, и возможности технического оснащения урока достаточные.
Конечно, основную роль, по прежнему, играет подготовленность учителя к уроку.
Слайд 3
Каждая новая тема урока математики, каждый раздел и
закон можно сопроводить исторической справкой, рассказать о необходимости возникновения
того или иного вопроса и его разрешения в истории математики. Это определённым образом ставит перед учащимися проблему, которую нужно решить на уроке. Важна здесь и мотивация изучения данной темы, пример из жизни, развитие в будущем данного вопроса и т.п.. Например, при изучении записи чисел в можно рассказать о возникновении десятичной системы счисления.
Слайд 4
Возникла десятичная система счисления в VIII веке в
Индии, позже была завезена в Китай из арабских стран,
отсюда и начали считать её арабской. Существуют и другие системы счисления, такие как восьмеричная, шеснадцатиричная и, наконец, двоичная изучаемая и используемая в информатике. В наши дни сохранилась ещё и римская запись чисел, иногда мы употребляем в разговорной речи слово «дюжина». При изучении чисел можно рассказать о числах- великанах и числах – лилипутах. Например «Миллион», «миллиард» - происходят от итальянского слова «Милле» - увеличенная тысяча.
Слайд 5
Попросите ребёнка поставить в тетради миллион точек. Думаю,
эта шутка будет понятна. Человек, увеличенный в миллион раз,
растянулся бы от Финского залива до Крыма. Миллиард – одно из самых молодых названий чисел. Оно вошло в употребление со времени окончания франко-прусской войны (1871г), когда французом пришлось уплатить Германии контрибуцию в 5 миллиардов франков. Миллиард минут составляет 19 столетий. А вы не знали? Попытаться сравнить эти числа с добычей газа и нефти, а затем сравнить числа великаны с числами лилипутами, т.е. с единицей делённой на миллион или миллиард.
Слайд 6
А если говорить о времени? Тысячная доля секунды,
казалось бы, не имеет в жизни особого значения, и
за такой промежуток времени ничего не успеешь сделать. Однако звук в воздухе передаётся в течение 1000-й доли секунды на 33 сантиметра.
Для современного физика миллионная доля секунды играет не менее важную роль, чем час на любом производстве. Особенно, если рассматривать колебания волн, световые, магнитные, электрические. Тем, более рентгеновские лучи, проникающие через многие непрозрачные тела. Частота их колебаний 2500 триллионов в секунду.
Слайд 7
? Интересно, так же, изучаемое в школе, понятие «приближённое
число». ?
Абсолютно точно измерить что-либо в природе невозможно, так
как сами меры или измерительные приборы не достаточно точны, да и человечество открывает всё новые и новые горизонты. Нет двух совершенно одинаковых килограммовых гирь или метровых линеек.
Слайд 8
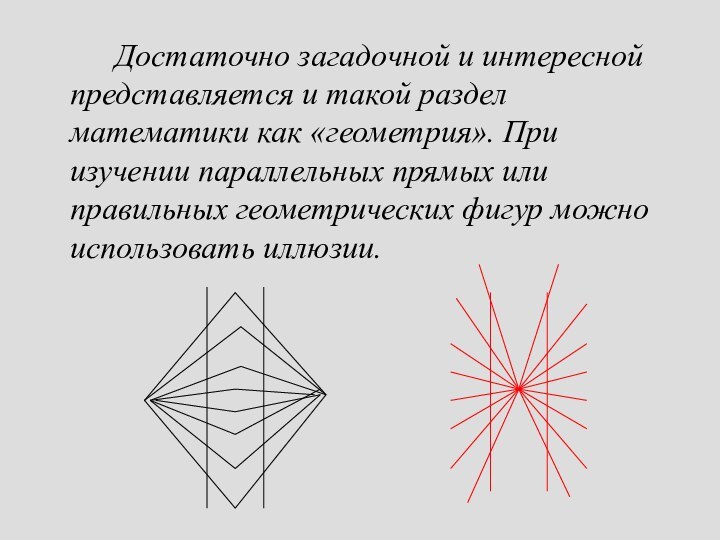
Достаточно загадочной и интересной представляется и такой раздел
математики как «геометрия». При изучении параллельных прямых или правильных
геометрических фигур можно использовать иллюзии.
Слайд 9
Все вертикальные прямые параллельны.
Слайд 10
Нередко, решая в школе какие-либо задачи, учащиеся младших,
средних классов делают вывод лишь на основании того, что
они водят на чертеже; часто они даже уверены, что после этого никаких доказательств уже не нужно. Но вот несколько примеров, когда наблюдение над чертежом может нас привести к грубо ошибочным выводам.
Разве вам не кажется, что
четырехугольник,
изображенный на Рисунке1
— трапеция (у которой
«верхнее» основание
меньше «нижнего»)?
Слайд 11
А на самом деле это квадрат! Линия на
рисунке 2, расположенная за двумя параллельными полосками, кажется ломаной,
а на самом деле —это прямая! Параллельны ли заштрихованные прямые (рис.4). Ответ: Да! Стороны прямоугольника кажутся кривыми! (рис.3).Кривыми кажутся также стороны треугольника! (рис.5).
Слайд 12
Хорошо проводить математические экскурсии. Например, математика в парке
( в поле, в лесу, у реки и т.п.)
Наблюдение различных геометрических фигур в природе. Составление планов участка. Решение более трудных задач на вычисление и построение на местности. Или математические сочинения, которые являются прекрасным средством для повышения у учащихся интереса к математике, улучшения их навыков в решении задач, своеобразный стимул к повторению пройденного. Это, пожалуй, наиболее доступная форма дополнительной работы с хорошо успевающими учащимися.
Слайд 13
Вводя число π «пи» можно рассказать о пирамиде
Хеопса или при изучении площади круга рассказать о древнейшей
задаче геометрии «о квадратуре круга». Решая геометрические задачи на построение можно вспомнить о первом греческом учёном Фолесе Милетском (624-547 гг до н.э.). Он вычислил высоту египетской пирамиды по отбрасываемой ею тени, умел измерять недоступные расстояния. Уделял внимание геометрии и великий философ, основатель «Академии» в Афинах Платон. У входа в Академию, как гласит легенда, он велел написать: «Пусть не входит сюда тот, кто не знает геометрии».В книге Евклида «Начало» находятся почти все задачи на построение, которые изучаются в настоящее время в школе. Хотя жил он в III веке до н.э..
Слайд 14
Внести элементы занимательности на уроке можно при изучении
каждой темы. Например, ученики не понимают, почему нуль не
пустое множество. Для объяснения этого можно привести классический пример, когда в коробку, за минуту до полудня, кладут числа от 1 до 10 и число 1 вынимается обратно. За ½ минуты до полудня кладут числа от 11 до 20, и число 2 вынимается обратно. За 1/3 минуты до полудня кладутся числа от 21 до 30 и число 3 вынимается обратно, и т.д.. Сколько чисел остаётся в ящике в полдень? Ответ: ни одного. Какое бы мы ни назвали число, например 106, оно отсутствует в ящике, т.к. оно вынимается при сто шестой операции. Значит, мы получаем пустое множество.
Слайд 15
В старших классах будет интересно сравнение евклидовой и
неевклидовой геометрии. Показать их различие и жизненность обоих. По
Лобачевскому не единственность прямой параллельной данной можно рассказать на примерах сущностей, обитаемых в разной среде, с разной плотностью атмосферы.
При изучении комплексных чисел использовать историю их возникновения. Многие учёные не признавали комплексные числа и частности Леонард Эйлер, который писал: «Квадратные корни из отрицательных – ввиду того, что они не более не менее и не равны нулю,- не могут быть причислены к возможным числам.» А Готфрид Лейбниц (1646-1716 гг.) даже завещал начертать на своей могиле знак как символ потустороннего мира.
Слайд 16
Однако жизнь доказывает их возможность. С помощью комплексных
чисел изучают многие явления природы, такие как плоские течения
жидкости, строят карты земной поверхности. Комплексные числа использовали Чаплыгин, Жуковский, Келдыш в теории самолётов.
Делает интересными уроки математики и введение вероятностных задач, измерение вероятности событий (испытаний). А при изучении наибольшего и наименьшего значения квадратного трёхчлена можно привести рассказ А.Толстого «Много ли человеку земли нужно», где сравниваются площади квадрата и других геометрических фигур с одинаковым периметром