Слайд 2
Содержание:
1. Текущий контроль.
2. Введение: Базовые концепции.
3. Часть 1:
Модели, описывающие
удаленные взаимодействия
и геометрию стабильных
тел.
4. Часть 2: Иллюзии сжимающихся
планет.
5. Выводы.
Слайд 3
Текущий контроль
Пользуясь методом эталонов, ранжировать вершины графа:
Слайд 5
Учитываемые факты:
1. Твердые тела со временем
сохраняют свои размеры и геометрию.
2. Галактики
«разбегаются», причем скорость убегания прямо пропорциональна расстоянию до Земли (закон Хаббла открыт в 30-х годах прошлого века Эдвином Хабблом).
3. Диаметр Луны за последние 800 млн. лет уменьшился на 110 – 180 м. (открыто лунным орбитальным телескопом в августе 2010 г.)
4. Семь млрд. лет назад ускорение, фиксируемое земным наблюдателем, с которым разлетались галактики, равнялось бы нулю.
5. Один метр равен одной десятимиллионной доле расстояния от южного полюса до северного по парижскому меридиану.
Слайд 6
Определение стабильности
Тело «В» в системе
координат А считается стабильным или твердым, если с точки
зрения внутреннего наблюдателя этой системы геометрия ( объем, площадь поверхности, кратчайшее расстояние между двумя любыми точками и.т.п.), этого тела не являются функциями времени.
Слайд 7
ЧАСТЬ 1
Модели, описывающие удаленные взаимодействия и геометрию стабильных
тел
Слайд 8
Определение расстояния между двумя точками
Измеренное расстояние L(a, b)
между материальными точками “a” и “b” равно отношению расстояния
R(a,b) между этими точками к эталону длины r (рис. 1):
L(a,b)=R(a,b)/r (1)
R(a, b)
r r r r
a
b
Рис. 1
Слайд 9
Традиционный подход
Традиционное использование эталона длины
для определения
расстояния и
скорости:
r =
const.
Слайд 10
Определение скорости движения точек относительно друг друга при
условии, что
r = var.
Из (1) следует скорость изменения
расстояния между точками «а» и «b»:
Закон Хаббла (для космических объектов «а» и «b»:
где Н – постоянная Хаббла:
Слайд 11
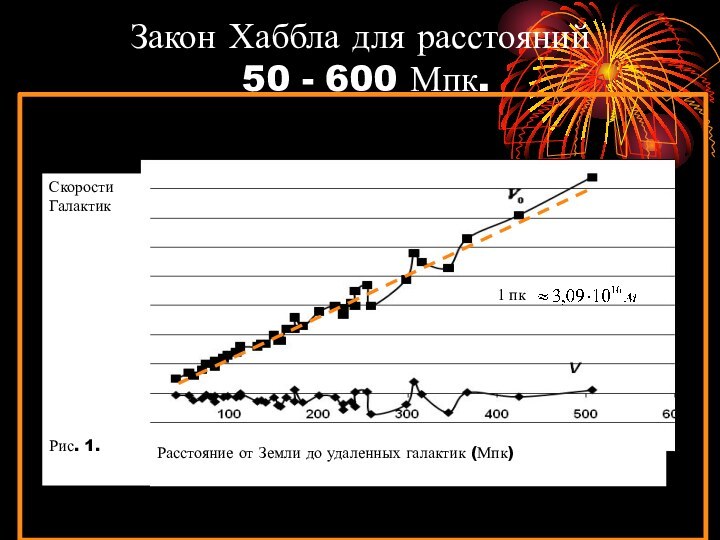
Закон Хаббла для расстояний
50 - 600
Мпк.
Расстояние от Земли до удаленных галактик (Мпк)
Скорости
Галактик
Рис. 1.
1
пк
Слайд 12
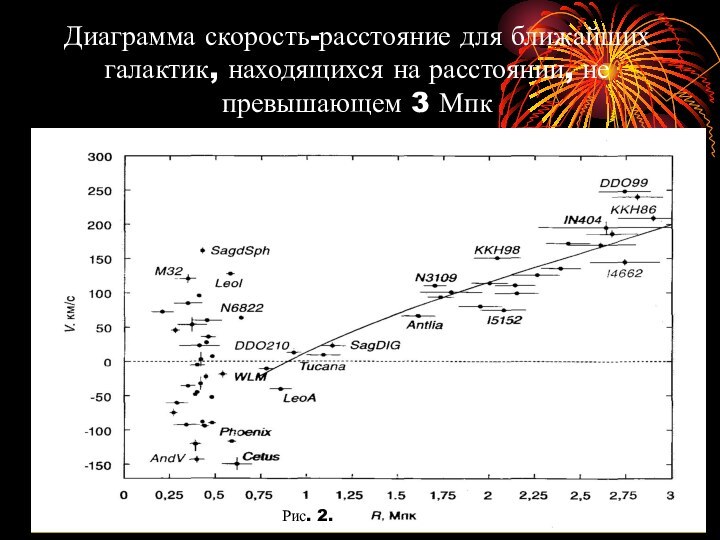
Диаграмма скорость-расстояние для ближайших галактик, находящихся на расстоянии,
не превышающем 3 Мпк
Рис. 2.
Слайд 13
Система уравнений (1) – (3)
Объединяя уравнения (1) –
(3), получим систему:
R(a,b) – действительное расстояние между точками «а»
и «b»:
r – эталон длины.
Слайд 14
Геометрия твердых тел
Решением системы (1) - (3) является:
Так как в качестве эталона измерения расстояния может
быть использовано расстояние между точками «а» и «b» любого твердого тела, то справедливо:
Слайд 15
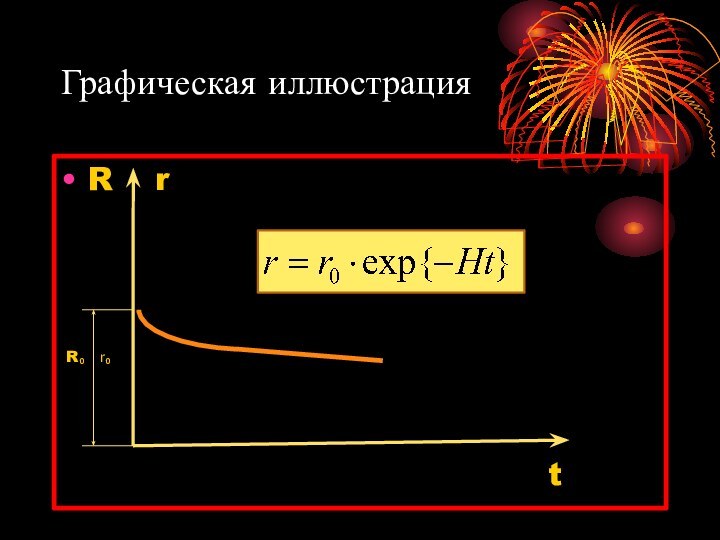
Графическая иллюстрация
R r
t
R₀ r₀
Слайд 16
Выводы:
Все эталоны длины со временем сжимаются в соответствии
с (4).
Все твердые тела со временем сжимаются в соответствии
с (5).
Непосредственно, пользуясь эталоном длины, сжатие твердых тел обнаружить невозможно:
R/r = R₀∙exp(-Ht)/ r₀∙exp(-Ht) =R₀/r₀ = const.
Слайд 17
Часть 2
Иллюзии сжимающихся планет
Слайд 18
Иллюзия стабильности размеров твердых тел
Отношение расстояния между точками
«а» и «b» любого твердого тела и эталона длины
r согласно (4) и (5) постоянно:
Слайд 19
Земля и Луна
Луна:
Постоянная Хаббла на Луне:
Земля –
постоянная Хаббла равна:
Слайд 20
Самостоятельно
Пользуясь данными предыдущего слайда, построить графики
отношений D₀ и D – диаметров Земли и Луны
за последние 3 млрд. лет, как функции времени с шагом 0,5 млрд. лет и сравнить их. Учесть, что диаметр Земли по экватору равен 12756 км., а по меридиану от южного до северного полюса – 12714 км., возраст Вселенной ≈ 13,7 млрд. лет = 1/Н (сек).
Слайд 21
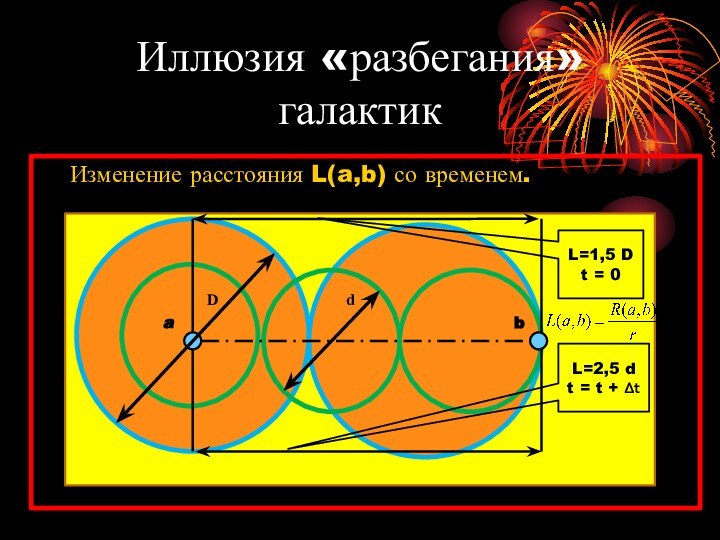
Иллюзия «разбегания» галактик
Изменение расстояния L(a,b) со
временем.
L=1,5 D
t = 0
L=2,5 d
t = t + ∆t
a
b
D d
Слайд 22
Аналитическая зависимость
Если космические объекты неподвижны друг
относительно друга, т. е. если dR/dt = 0, то,
с учетом (6), справедливо :
Т.о. наблюдатель на одном из них зафиксирует их взаимное удаление, отвечающее закону Хаббла.
Слайд 23
Гравитационное торможение и иллюзорное ускорение
Величины гравитационного торможения галактик
«G» и ускорения «А», вызванного сокращением эталона длины, определяются
системой:
Слайд 24
Обозначения, принятые в системе (8)
γ – гравитационная
постоянная
ρ – средняя плотность материи во Вселенной
;
Ŗ - радиус видимой Вселенной
(Ŗ = сТ, где «с» – скорость света,
Т – время существования
Вселенной ).
Слайд 25
Самостоятельно
Построить графики G(T) и А(Т) и определить время,
когда суммарное ускорение равнялось нулю.
Слайд 26
Графики зависимостей величин A, G и α от
возраста Вселенной Т.
Слайд 27
Выводы 1:
Имеет место экспоненциальное сокращение размеров физических объектов,
которое непосредственно не фиксируется благодаря синхронному сокращению эталонов, используемых
для измерения расстояний.
Закон Хаббла можно объяснить экспоненциальным сокращением со временем эталонов, применяемых для измерения расстояний, в том числе уменьшением диаметра Земли.
Слайд 28
Выводы 2
Сжатие Луны, зафиксированное НАСА благодаря снимкам Lunar
Reconnaissance Orbiter Camera в августе 2010 года, позволяет определить
«лунную» величину постоянной Хаббла, которая хорошо коррелирует с диапазоном, в котором эта величина заключена, определенным в земных условиях.
Слайд 29
Выводы 3
В отсутствие внешних воздействий на каждое из
двух покоящихся на фиксированном расстоянии, с точки зрения наблюдателя
в системе координат тел, другой наблюдатель на одном из них, пользуясь системой координат «своего» тела , зафиксирует спонтанное увеличение расстояния между этими телами, отвечающее закону Хаббла.