Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

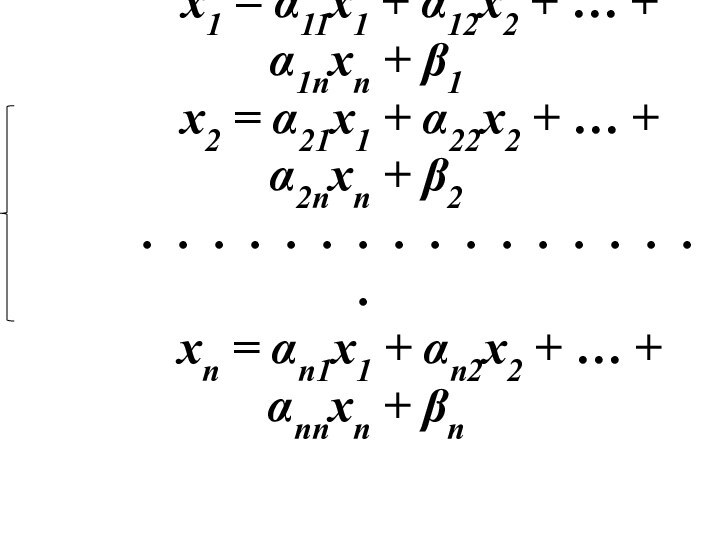
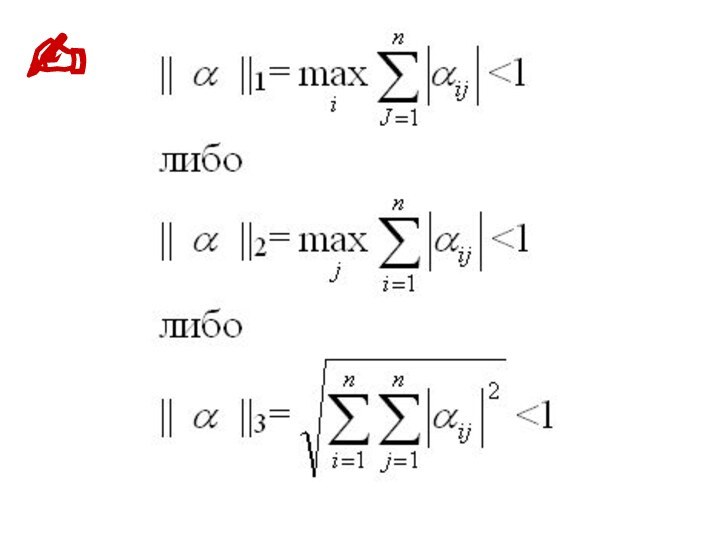
Презентация на тему Метод интерации

Содержание

Обозначим:
Метод итерации Обозначим: x1 = α11x1 + α12x2 + … + α1nxn + β1x2 = Обозначим:и нулевое приближение Х(0), Х(1), …, Х(k) Итерационная последовательность Пример 1. Решить систему методом итерацииРешение x(0) (0;0;0) - нулевое приближение x(1) (-1;-2;-3) - первое приближение x(2) (1;-2;-2) - второе приближение Условия сходимости итерационного процесса или Пример 2: Проверить сходимость итерационного процесса для системы.Решение=0+0,2+0,2=0,4 ✍ Матрица А=[aij] определяется тремя нормами: Оценка погрешности приближенного процесса метода итерации Пример 3. Привести систему к нормальному виду7,6 х1 +0,5 х2 +2,4 х3
Слайды презентации

Слайд 2

Слайд 3 Обозначим:

Обозначим:

Слайд 4 x1 = α11x1 + α12x2 + … +

x1 = α11x1 + α12x2 + … + α1nxn + β1x2

α1nxn + β1
x2 = α21x1 + α22x2 + …

+ α2nxn + β2
. . . . . . . . . . . . . . . . .
xn = αn1x1 + αn2x2 + … + αnnxn + βn


Слайд 5 Обозначим:
и

Обозначим:и

Слайд 6 нулевое приближение

нулевое приближение

Слайд 7 Х(0), Х(1), …, Х(k)
Итерационная последовательность

Х(0), Х(1), …, Х(k) Итерационная последовательность

Слайд 8 Пример 1.
Решить систему методом итерации

Решение


Пример 1. Решить систему методом итерацииРешение

Слайд 9 x(0) (0;0;0) - нулевое приближение


x(1) (-1;-2;-3) -

x(0) (0;0;0) - нулевое приближение x(1) (-1;-2;-3) - первое приближение

первое приближение

Слайд 10 x(2) (1;-2;-2) - второе приближение

x(2) (1;-2;-2) - второе приближение

Слайд 11 Условия сходимости итерационного процесса


или

Условия сходимости итерационного процесса или

Слайд 12 Пример 2: Проверить
сходимость итерационного
процесса для системы.
Решение
=0+0,2+0,2=0,4

Пример 2: Проверить сходимость итерационного процесса для системы.Решение=0+0,2+0,2=0,4

Слайд 13 ✍

✍

Слайд 14 Матрица А=[aij] определяется тремя нормами:

Матрица А=[aij] определяется тремя нормами:

Слайд 15 Оценка погрешности приближенного
процесса метода итерации


Оценка погрешности приближенного процесса метода итерации
  • Имя файла: metod-interatsii.pptx
  • Количество просмотров: 132
  • Количество скачиваний: 0
- Предыдущая Системная теория Никласа Лумана
Следующая - Фауна Палеарктического подцарства

Похожие презентации

Тема самообразования Графические диктанты на уроках математики Тема самообразования Графические диктанты на уроках математики 153
Числовий вираз. Числові рівності та нерівності Числовий вираз. Числові рівності та нерівності 117
Задачи на смекалку для младших школьников олимпиадные задания по математике (3 класс) Задачи на смекалку для младших школьников олимпиадные задания по математике (3 класс) 160
Презентация по математике Прямоугольник. Квадрат Презентация по математике Прямоугольник. Квадрат 113
Теория принятия решений Теория принятия решений 133
Решение квадратных уравнений 8 класс Решение квадратных уравнений 8 класс 91
Математика. 1 класс. Урок 1. Цвет. Знакомство с радугой презентация к уроку по математике (1 класс) Математика. 1 класс. Урок 1. Цвет. Знакомство с радугой презентация к уроку по математике (1 класс) 129
Задачи по математике 2 класс Задачи по математике 2 класс 110
Открытый урок Действия с десятичными дробями 5 класс ( по программе Н.Я. виленкина) Открытый урок Действия с десятичными дробями 5 класс ( по программе Н.Я. виленкина) 183
Число 3 Число 3 164
Программа внеурочной деятельности учащихся начальной школы Загадочная геометрия рабочая программа по математике (3 класс) Программа внеурочной деятельности учащихся начальной школы Загадочная геометрия рабочая программа по математике (3 класс) 165
Логарифмическая функция ее свойства и график Логарифмическая функция ее свойства и график 117
Лента Мебиуса.Все гениальное просто. Лента Мебиуса.Все гениальное просто. 165
Презентация Электронное портфолио Вигель С.В., учителя математики Презентация Электронное портфолио Вигель С.В., учителя математики 135
Сентябрь. 1-е занятие в средней группе презентация к уроку по математике (средняя группа) Сентябрь. 1-е занятие в средней группе презентация к уроку по математике (средняя группа) 134
Разработка НОД по ФЭМП Путешествие на волшебном паровозике методическая разработка по математике (младшая группа) Разработка НОД по ФЭМП Путешествие на волшебном паровозике методическая разработка по математике (младшая группа) 125
Свойства функции у = tg х и ее график Свойства функции у = tg х и ее график 123
Уравнения, сводящиеся к квадратным Уравнения, сводящиеся к квадратным 121
Счет предметов, математика, 1 класс презентация к уроку по математике (1 класс) по теме Счет предметов, математика, 1 класс презентация к уроку по математике (1 класс) по теме 108
делители и кратные делители и кратные 114
КВН по математике во 2 классе КВН по математике во 2 классе 156
Весёлые примеры презентация к уроку по математике (2 класс) по теме Весёлые примеры презентация к уроку по математике (2 класс) по теме 146
Презентация по математике на тему:Наименьшее трёхзначное число (2 класс). Презентация по математике на тему:Наименьшее трёхзначное число (2 класс). 212
Методы решения геометрических задач ЕГЭ, задание С2 (Расстояние от точки до плоскости) Методы решения геометрических задач ЕГЭ, задание С2 (Расстояние от точки до плоскости) 126
Конкурсный урок математика 2 класс Конкурсный урок математика 2 класс 116
Презентация по математике Десятичные дроби для 6 класса Презентация по математике Десятичные дроби для 6 класса 124
Умножение на двузначное и трехзначное число Умножение на двузначное и трехзначное число 50
Урок и презентация по математике на темуСовершенствование вычислительных умений. Решение задач Урок и презентация по математике на темуСовершенствование вычислительных умений. Решение задач 110
Действия с натуральными числами Действия с натуральными числами 94
Математика 1 класс Сложение и вычитание числа 2 план-конспект урока по математике (1 класс) по теме Математика 1 класс Сложение и вычитание числа 2 план-конспект урока по математике (1 класс) по теме 110