- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Метод интервалов. Общий метод интервалов
Содержание
- 2. Литература С.М. Никольский «Алгебра и начала анализа:
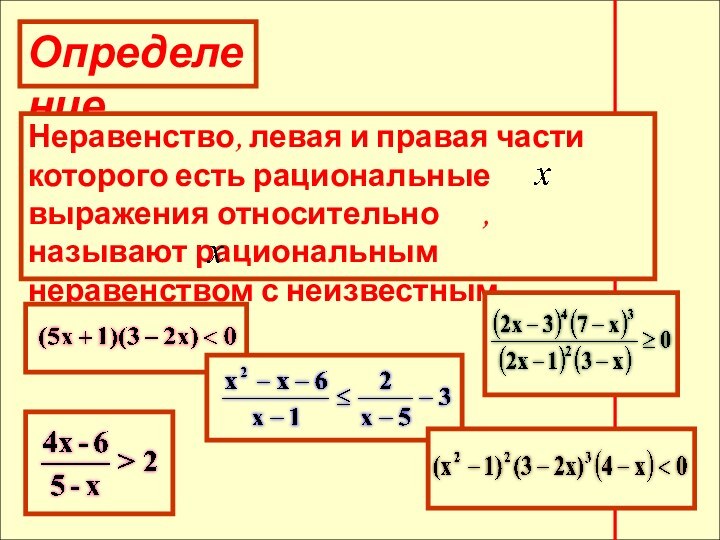
- 4. Определение
- 7. +-+-+
- 9. Метод интервалов для решения
- 10. 3. Над промежутком справа
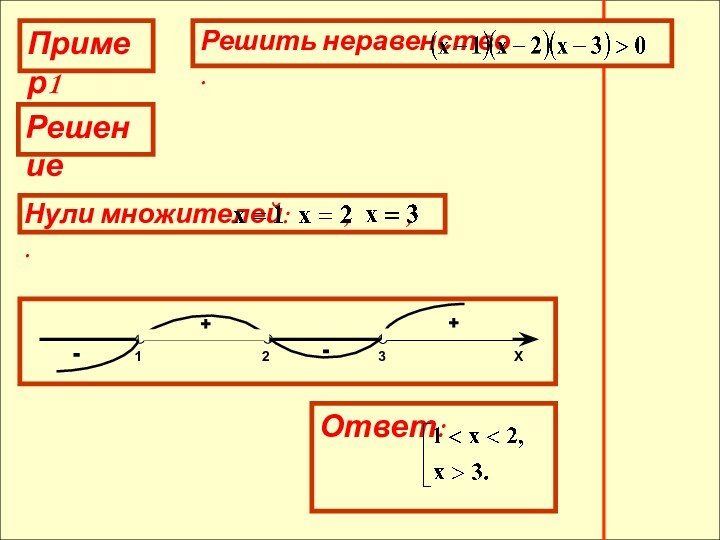
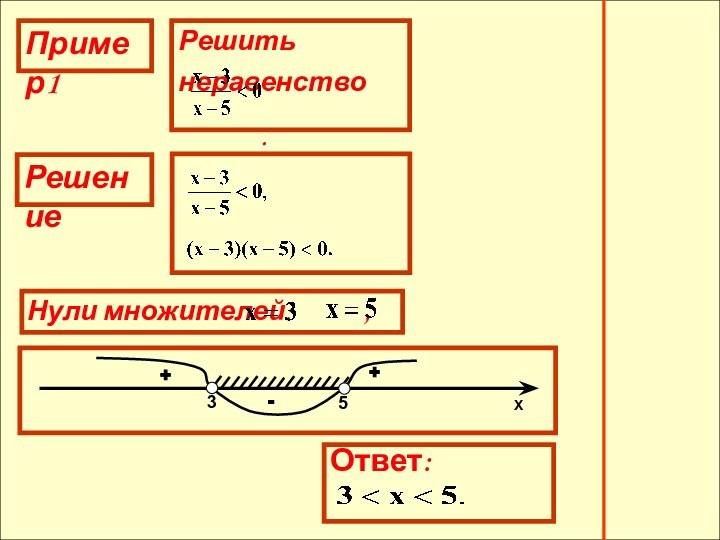
- 11. Пример1Решение+-+-
- 12. Пример2Решениеумножив неравенство на -1
- 13. Пример3Решениеумножив неравенство на -1
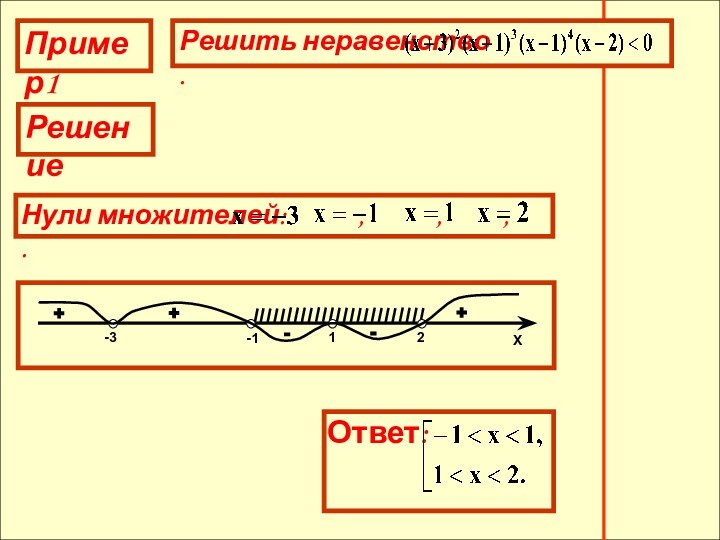
- 14. Пример4РешениеНули множителей:
- 15. Общий метод интервалов для
- 16. Общий метод интервалов для
- 17. РешениеНули множителей:
- 18. +--+
- 20. Нули множителей:
- 21. умножив неравенство на -1
- 22. Нули множителей:
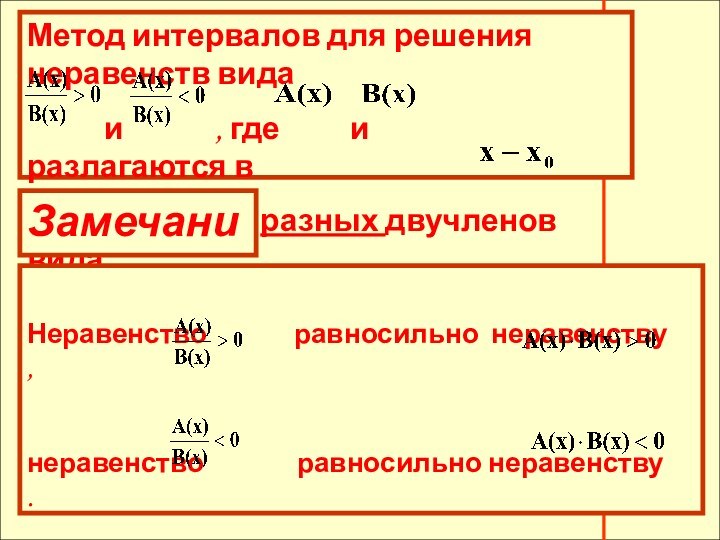
- 23. Метод интервалов для решения
- 24. Нули множителей:
- 27. Нули числителя:
- 28. Скачать презентацию
- 29. Похожие презентации
Литература С.М. Никольский «Алгебра и начала анализа: Учебник для 10 класса общеобразовательных учреждений» §2 п. 2.7 – 2.9.























Слайд 10
3. Над промежутком справа от
наибольшего нуля многочлена поставить знак «+», так как на
этом промежутке все множители положительны. Затем, двигаясь справа налево, при переходе через очередной нуль, сменить знак на противоположный.
Слайд 12
Пример2
Решение
умножив неравенство на -1 и
разложив квадратный трёхчлен на множители, получим неравенство равносильное данному
Нули
множителей: , , , . +
-
+
-
+
Слайд 13
Пример3
Решение
умножив неравенство на -1 и
разложив квадратные трёхчлены на множители, получим неравенство равносильное данному
Нули
множителей: , , , . +
+
-
-
+
Слайд 16
Общий метод интервалов для решения
неравенств вида ,
, , ,где, если не все различны.
3. Над промежутком справа от наибольшего нуля многочлена поставить знак «+», так как на этом промежутке все множители положительны. Затем, двигаясь справа налево, при переходе через очередной нуль, сменить знак на противоположный, если соответствующий этому нулю двучлен возведён в нечётную степень, и сохранить знак, если соответствующий этому нулю двучлен возведён в чётную степень.
Слайд 21
умножив неравенство на -1 и
разложив квадратные трёхчлены на множители, получим неравенство равносильное данному
Нули
множителей: , , , . +
-
+
-
+
Слайд 23
Метод интервалов для решения неравенств
вида
и
, где и разлагаются в произведения двучленов, где в числителе и знаменателе дроби имеются одинаковые двучлены .