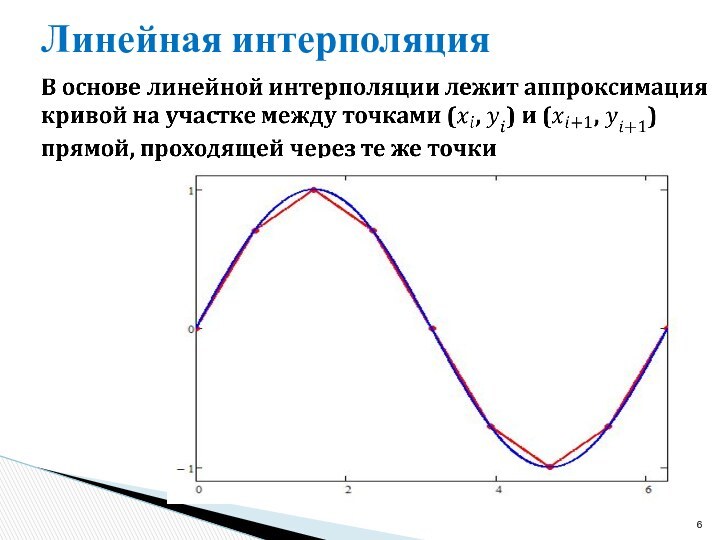
должна пройти через все точки
Регрессия - аппроксимирующая функция не
обязательно должна проходить через все точкиЦель
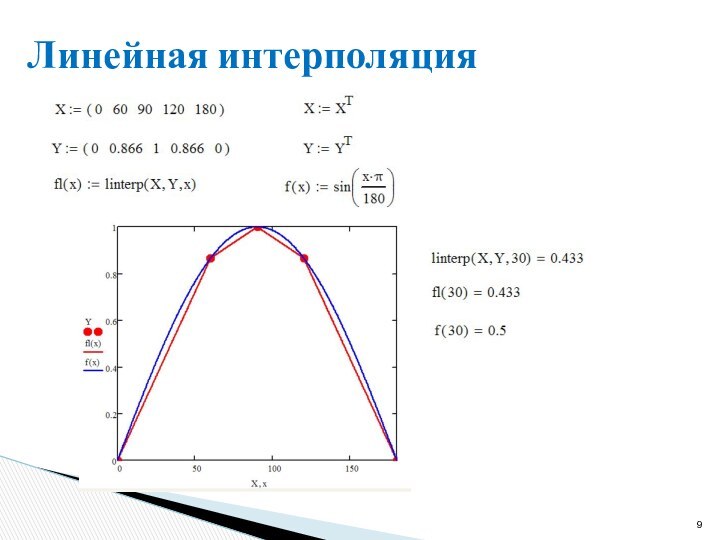
Получение функциональной зависимости y = f(x)
Числовые данные
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть













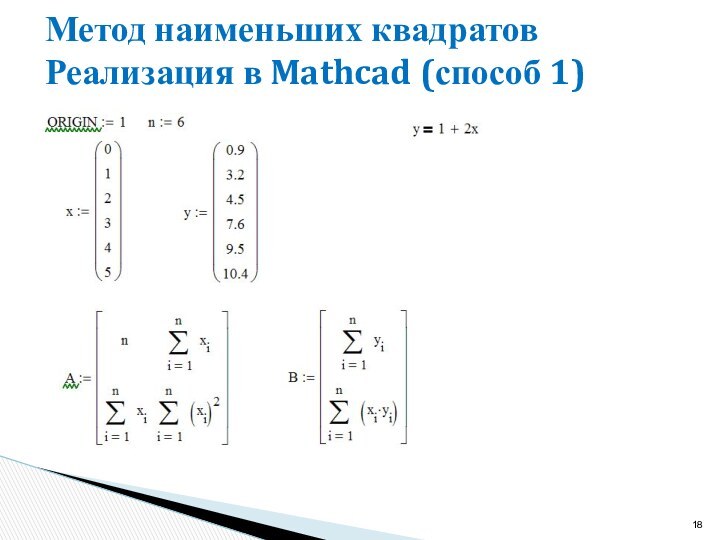
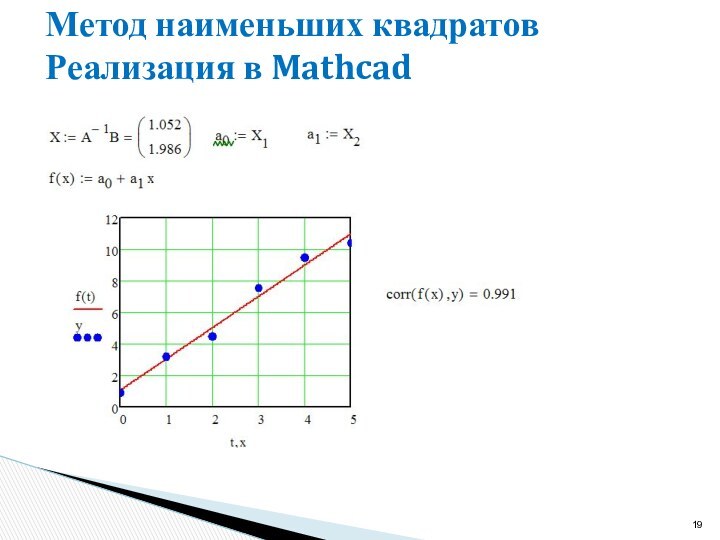




Цель
Получение функциональной зависимости y = f(x)
Числовые данные
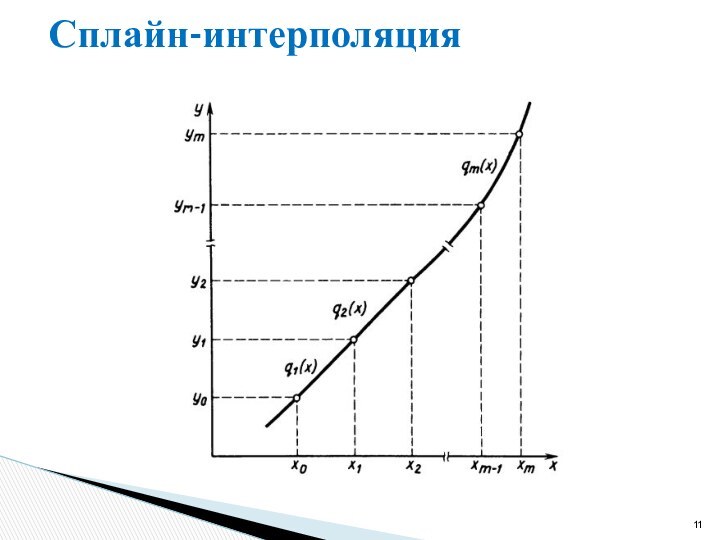
для внутренних точек
для двух внешних
Система уравнений – трехдиагональная
Для решения таких систем используется метод прогонки
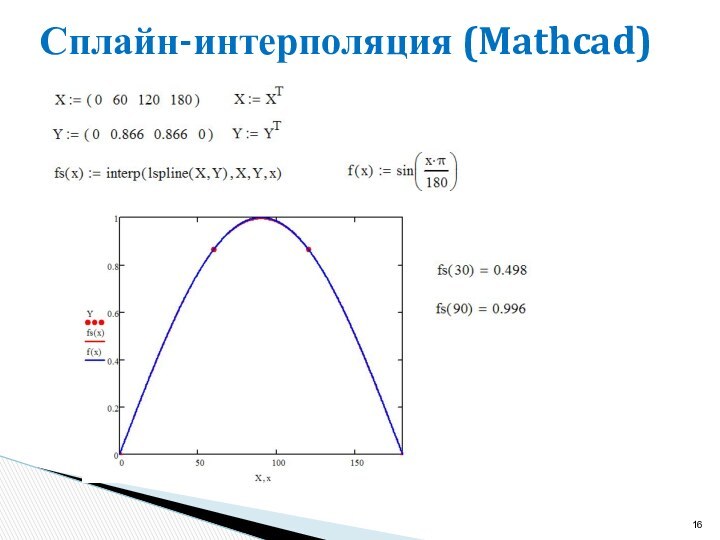
lspline(X,Y) – создает вектор коэффициентов кривой, которая приближается к прямой линии в граничных точках;
pspline(X,Y) – создает вектор коэффициентов кривой, которая приближается к квадратичной параболе в граничных точках;
cspline(X,Y) – создает вектор коэффициентов кривой, которая приближается к кубической параболе в граничных точках.