Слайд 2
Кудрявцев Л.Д. Курс математического анализа, т.1-2
Ильин В.А., Поздняк
Э.Г. Основы математического анализа, т.1-2 Никольский С.М. Курс математического
анализа т.1-2
Письменный Д.Т. Конспект лекций по высшей математике ч.1-2
Берман Г.Н. Сборник задач по курсу математического анализа Математический анализ в примерах и задачах (Учебник НГТУ) Типовые расчеты 1,2, 3
Слайд 7
Ларин А.А.
К У Р С
В Ы С Ш
Е Й
М А Т Е М А Т И
К И
2000
http://alexlarin.narod.ru/kvm.html
Слайд 8
Изучение математики
- совершенствует общую культуру мышления, дисциплинирует ее,
приучает человека логически рассуждать, воспитывает точность и обстоятельность аргументации;
-
позволяет не загромождать исследование ненужными подробностями,
не влияющими на сущность дела, и, наоборот, не пренебрегать тем, что имеет принципиальное значение для существа изучаемого вопроса;
- развивает умение логически мыслить, владение математическим аппаратом, правильное использование которого дает в руки человека мощный метод исследования и большую экономию мышления.
.
Слайд 9
1. МНОЖЕСТВА
- знак принадлежности
- квантор всеобщности
-
квантор существования
- знак логического следования
- символ эквивалентности
Λ
- символ конъюнкции (и)
V- символ дизъюнкции (или)
(a∈ A)
(∀x ∈ M )
(∃x∈M:)
(a⇒b)
Логические символы.
∀ΔABC : AC = BC ⇒ ∠A = ∠B
Слайд 10
Множества. Способы задания.
def
A={a,b,c,d};
A ={x P( x)};
{a} - одноэлементное
множество;
- пустое множество
Действительные корни уравнения x2 +1 =0 образуют
пустое множество
множества конечные и бесконечные. Множество характеризуется мощностью
Если A - конечное множество, то мощность множества A – это число его элементов.
Слайд 11
Отношения между множествами.
Определение 1.1. Множества A и B
называются равными, если каждый элемент множества A является элементом
множества B и, наоборот, каждый элемент множества B является элементом множества A.
■
Обозначают A=B.
Пример:
A = { x
( x −1) ⋅ ( x − 2) ⋅ ( x − 3) = 0 },
x < 4 }.
B = { x ∈ N A = B
Слайд 12
Свойства равенства:
A=A
A=B, B=C A=C
A=B B=A
(рефлексивность); (транзитивность);
(симметричность).
Неравенство множеств обозначают
■
A B.
Слайд 13
Определение 1.2.
Множество A (A ) называется подмножеством
множества B (B
), если каждый элемент множества A
является элементом множества B.
Обозначение: A B a A a B.
Если A B и A B A B.
Примечание
Пустое множество является подмножеством любого множества
Слайд 14
Операции над множествами.
V – основное или универсальное множество.
1)
В планиметрии V =R2
2) Для функций действительной переменной
V = R.
Определение
1.3. Объединением множеств A и B называется множество A B, содержащее те и только те элементы, которые принадлежат хотя бы одному из множеств A или B (или обоим одновременно).
def
AB={ x x∈A∨ x∈B∨( x∈ A∧ x∈B ) }
■Пример: A = {2,3,4,6}, B = {1,2,3,4,5,6} AB = {1,2,3,4,5,6}.
Слайд 15
Один из величайших
математиков
петербургской академии Леонард Эйлер
(1707–1783) за свою долгую
жизнь
написал более 850 научных работ.
В одной из них появились круги, которые “очень подходят
для того, чтобы облегчить наши размышления”. Эти круги и назвали кругами Эйлера.
Слайд 16
Джон Венн ( John Venn; 4 августа 1834,
Халл (Йоркшир) — 4 апреля 1923, Кембридж) — английский
логик и философ
Слайд 17
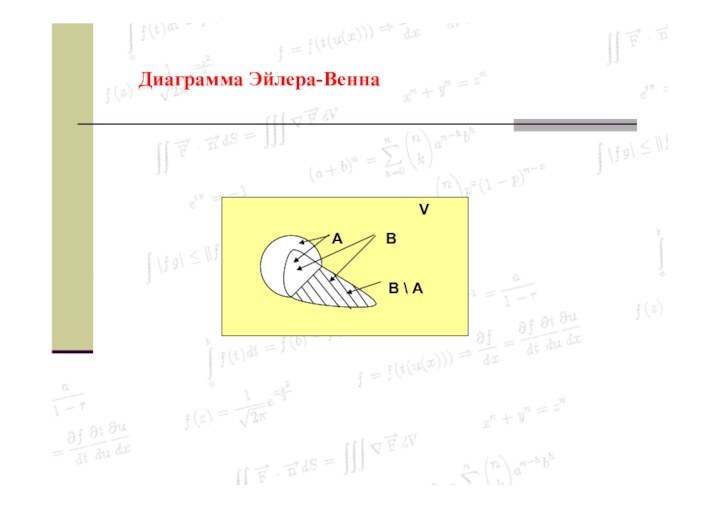
Диаграмма Эйлера-Венна
A B
V
A
B
Слайд 18
Свойства объединения множеств.
■ 1) A B = B
A
■ 2) A ( B C )
= ( A B ) C
(коммутативность), (ассоциативность).
Очевидно
■ A A = A,
A =A,
A V = V.
Слайд 19
Определение 1.4.
Пересечением множеств A и B называется множество
A B, состоящее из всех тех и только
тех элементов, каждый из которых принадлежит обоим множествам одновременно.
■ A B = { x x A x B }.
Слайд 20
Диаграмма Эйлера-Венна
V
A
B
A B
Слайд 21
Свойства пересечения множеств.
(коммутативность), (ассоциативность).
■ 1) A B =
B A
■ 2) A ( B C
) = ( A B ) C
Очевидно, что
■ A A = A, A = , A V = A.
Операции объединения и пересечения подчиняются дистрибутивным законам:
■ A ( B C ) = ( A B ) ( A C ),
■ A ( B C ) = ( A B ) ( A C ).
Слайд 22
Определение 1.5.
Разностью двух множеств B и A называется
множество B \ A, состоящее из всех тех и
только тех элементов, которые принадлежат B, но не принадлежат A.
■
B \ A = { x x B x A }.
Слайд 24
Определение 1.6.
Разность V \ A называется дополнением множества
A до
универсального множества V и обозначается
Примеры:
A
def
A =V \
A={ x| x∉A}.
A = A;
A A =V ;
∅ =V ;
A A = ∅ ;
V = ∅.
Слайд 26
Определение 1.7.
Пара элементов ( x ; y ),
x A, y B называется упорядоченной, если
указан порядок записи элементов x и y.
Считается, что
( x1 ; y1 )=( x2 ; y2 )⇔ x1 =x2 , y1 =y2 .
Слайд 27
Определение 1.8.
Декартовым или прямым произведением двух множеств A и B
называется множество, обозначаемое A B, состоящее из всевозможных упорядоченных
пар ( x ; y ).
■ A B = { ( x ; y ) | x A , y B }.
x
A
1
y
2
B
1
3
Рене Декарт(Rene Descartes)
Слайд 28
Несколько приятелей встретились на вокзале, чтобы поехать за
город в лес. При встрече все они поздоровались друг
с другом за руку.
Сколько человек поехало за город, если всего было10 рукопожатий?
Слайд 31
Отображение множеств. Эквивалентность множеств.
Пусть A и B -
произвольные множества.
Пусть f - закон (правило) по которому
a A b B.
Говорят, что задано отображение f A в B или оператор f
A в B.
Обозначение:
f : A B или
f
A → B .
b – образ элемента a (обозначают f(a) );
a – прообраз элемента b = f -1 (a).
Слайд 32
Определение отображения:
■ f : A B
a A b
B : b = f ( a ).
Множество образов всех элементов a A при отображении f называют
образом множества A при этом отображении и обозначают:
■ f(A)={ f(a) | aA } B.
Задание отображения – это задание тройки ( A, f, B ).
Множество упорядоченных пар (x, f(x)) - график отображения
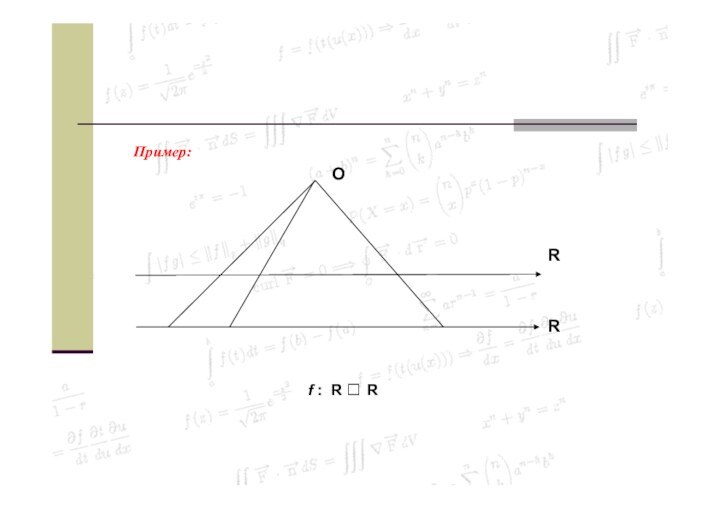
Слайд 33
Определение 1.9
Отображение называется инъекцией, если для любых элементов
x1, x2 ∈ X, для которых f(x1) = f(x2)
следует, что x1 = x2
Сюръекцией (или отображением "на" ) называется отображение, при котором f(X) = Y
Слайд 34
Биекция – это одновременно и сюръекция и инъекция,
т.е., отображение
f : A B называют биективным или
взаимно однозначным, если каждый элемент b B является образом только одного элемента a A.
A
B
Слайд 35
f – взаимно однозначное отображение
b B a
A : b = f ( a )
∀ a1 , a2 ∈ A a1 ≠ a2 ⇒ f ( a1 )≠ f ( a2 ).
■Если f - взаимно однозначное отображение, то можно говорить
■об обратном отображении.
Слайд 36
Определение 1.10.
Отображение f -1 : B→A называется
обратным к отображению
f : A→B , если каждому элементу
b B ставится в соответствие единственный элемент a A, образом которого при отображении f является b
f − 1 : B → A ⇔ ∀ b ∈ B ∃ 1 a ∈ A : a = f − 1 ( b )
.
Слайд 38
Определение 1.11
Два множества A и B называются эквивалентными (равномощными),
если существует хотя бы одно взаимно однозначное отображение одного множества
на другое.
Свойства эквивалентности:
A A A
A B B A A, B
A B, B C A C
A, B, C
(рефлексивность); (симметричность); (транзитивность).
Слайд 39
Числовые множества
Множества, элементами которых являются числа, называются числовыми.
Примерами
числовых множеств являются:
N = {1; 2; 3; ...; n;
... } - множество натуральных чисел;
Z = {0; ±1; ±2; ...; ±n; ...} - множество целых чисел;
Q = {m/n ; т ∈ Z, n ∈ N}- множество рациональных чисел. R - множество действительных чисел.
Между этими множествами существует соотношение
N Z Q R.
Слайд 40
выполняются: коммутативность, ассоциативность, дистрибутивность;
Множество натуральных чисел N.
■ N = {1,
2, 3, …}.
Свойства:
■ 1)
■
■
■
■
■
2) деление и вычитание не определены; 3)
1 N;
4) n N n + 1 N;
5) если M N, 1 M, n M и (n + 1) M, то M = N (аксиома индукции);
∀n ,n ∈N ⇒ n + n ∈N, n ⋅n ∈N
1 2 1 2 1 2
Множество, эквивалентное множеству натуральных чисел называется
счетным.
Если множество счетно, то его элементы можно занумеровать. Мощность счетного множества обозначают буквой c.
Слайд 41
Множество целых чисел Z
Z = { …, -2,
-1, 0, 1, 2, …}.
Свойства:
Определены операции сложения, умножения, вычитания;
Не определено деление;
Z – упорядоченно, т.е. имеет место
p1 < p2 ∨ p1 = p2 ∨ p1 > p2 ;
Z – счетно и бесконечно;
N Z Q.
Слайд 42
Множество рациональных чисел Q.
Q = { q =
p / n | p Z
, n N }.
Свойства:
Определены все арифметические операции;
Q – упорядоченно;
Q – плотно, т. е.
∀q1 , q2 ∈Q ∃q∈Q: q1 < q < q2 .
Q – счетно и бесконечно;
N Z Q R.
Слайд 43
Множество действительных чисел R.
■
■
■
Свойства:
R – упорядоченно;
R –бесконечно;
Множество R плотное:
между любыми двумя различными числами а и b содержится
бесконечное множество действительных чисел х, т. е. чисел, удовлетворяющих неравенству а < х < b.
Слайд 44
Множество R непрерывное.
Пусть множество R разбито на два
непустых класса А и В таких, что каждое действительное
число содержится только в одном классе и для каждой пары
чисел а А и b В выполнено неравенство а
Оно отделяет числа класса А от чисел класса В, Число с является либо наибольшим числом в классе А (тогда в классе В нет наименьшего числа), либо наименьшим числом в классе В (тогда в классе А нет наибольшего).
Это позволяет установить взаимно-однозначное соответствие между множеством всех действительных чисел и множеством всех точек прямой
Слайд 45
Последовательности
Определение 1.12
Пусть каждому натуральному числу n=1, 2, ...
приведено в соответствие в силу некоторого закона число хп.
Тогда говорят, что этим определена последовательность чисел x1, x2, …xn,.,. или, короче, последовательность {xi}
Отдельные снабженные номерами п (индексами) числа хп называют элементами последовательности {xi}. Они могут быть действительными или комплексными. Мы рассматриваем случай, когда они действительны.
Для разных п отдельные элементы последовательности могут оказаться равными как числа (хi = xj) Однако хi , xj рассматриваются как разные элементы последовательности.
Слайд 46
Примеры последовательностей:
В случае 7) не видно, как написать
общую формулу для произвольного элемента хп,
однако закон образования чисел
хn ясен:
Слайд 47
Определение 1.13
Последовательность {хп} называется ограниченной, если существует такое
число М > 0, что для любого n
N выполняется неравенство
В противном случае последовательность называется неограниченной.
Легко видеть, что последовательности 2,3,4 ограничены, a 1— неограничена
Определение 1.14
Последовательность {хп} называется возрастающей (неубывающей), если для любого n выполняется неравенство xn+1 > xn (xn+1 ≥ xn ).
Аналогично определяется убывающая (невозрастающая) последовательность.
Все эти последовательности называются монотонными
Слайд 48
Предел последовательности
Метод пределов есть основной метод, на котором
базируется математический анализ
Можно заметить, что члены последовательности
неограниченно приближаются к
числу 1.
.
В этом случае говорят, что последовательность иn стремится к пределу 1
Слайд 49
Определение 1.14
Число а называется пределом последовательности {xn} если
для любого положительного числа найдется такое натуральное число
N, что
при всех п > N выполняется неравенство
В этом случае пишут
или xn → a и говорят, что последовательность {хn} имеет предел, равный числу а
(или хn стремится к а). Говорят также, что последовательность {хп} сходится к а.
Слайд 50
Геометрический смысл определения предела последовательности.
Неравенство
равносильно неравенствам -
< хn - а < или а -
< хn < а + ,
которые показывают, что элемент хn находится в -окрестности точки а.
Поэтому определение предела последовательности геометрически можно сформулировать так: число а называется пределом последовательности {хп} если для любой ε-окрестности точки а найдется натуральное число N, что все значения xn, для которых п > N,
попадут в ε-окрестность точки а .