- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Определенные треугольники и их виды
Содержание
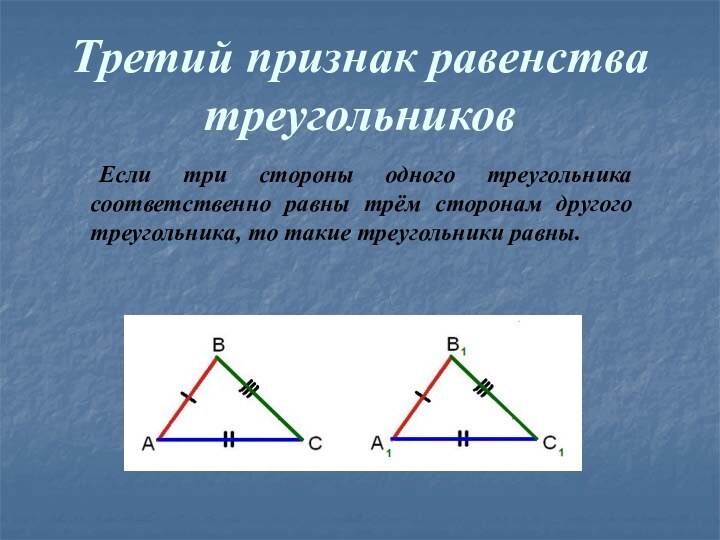
- 2. СодержаниеТреугольники. Определение треугольника. Виды треугольников. Медианы, биссектрисы и высоты треугольника. Признаки равенства треугольников
- 5. Виды треугольников (по сторонам)∆ MNK – равносторонний
- 6. Виды треугольников (по углам)∆ ABC – тупоугольный
- 7. Медианы треугольника Отрезок, соединяющий вершину треугольника с
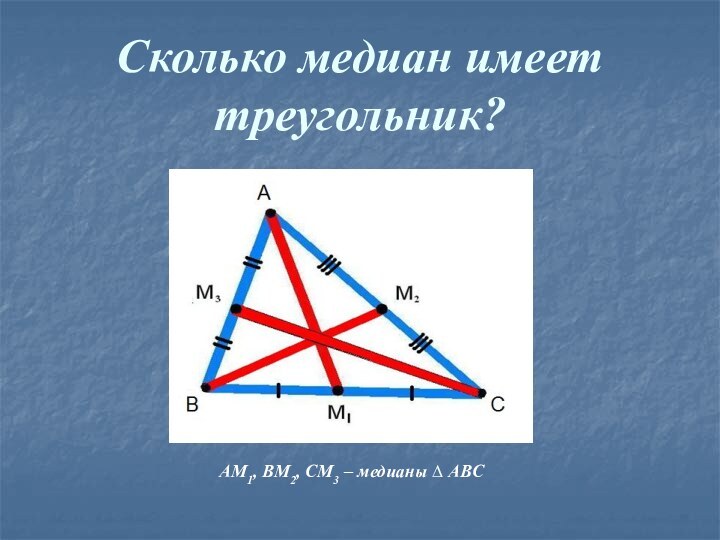
- 8. Сколько медиан имеет треугольник?AM1, BM2, CM3 – медианы ∆ ABC
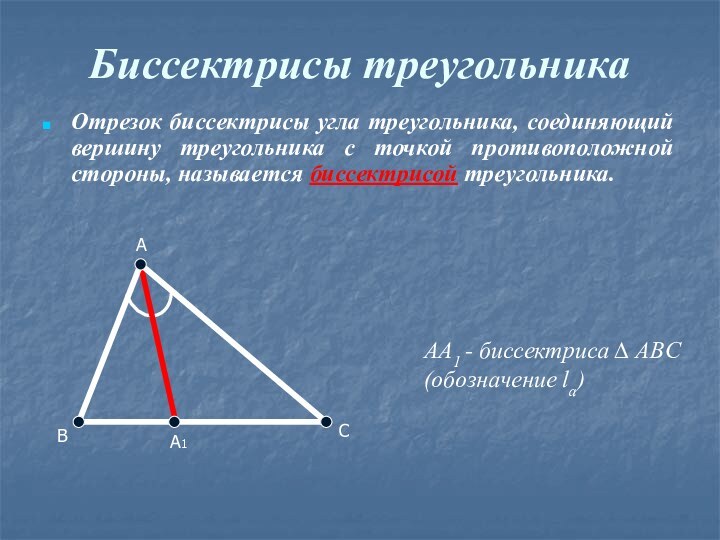
- 9. Биссектрисы треугольникаОтрезок биссектрисы угла треугольника, соединяющий вершину
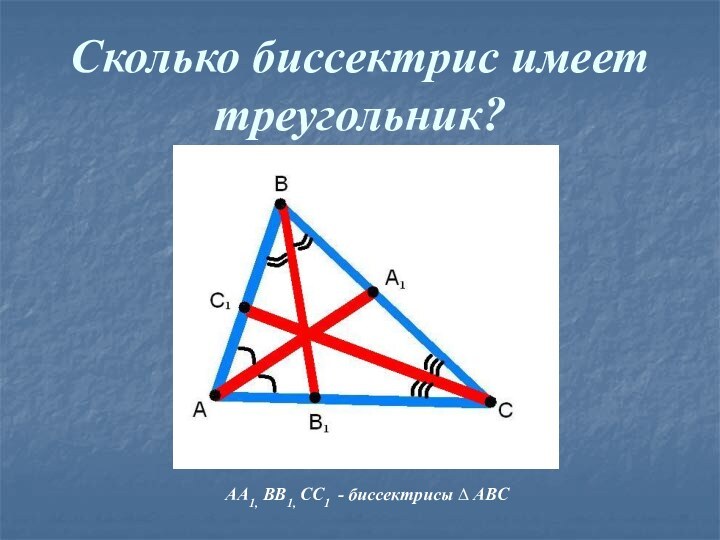
- 10. Сколько биссектрис имеет треугольник?AA1, BB1, CC1 - биссектрисы ∆ ABC
- 11. Высоты треугольникаПерпендикуляр, проведенный из вершины треугольника к
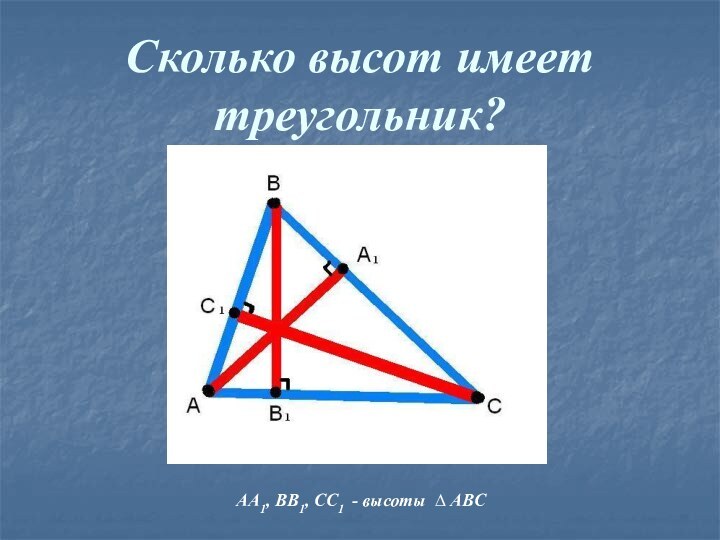
- 12. Сколько высот имеет треугольник?AA1, BB1, CC1 - высоты ∆ ABC
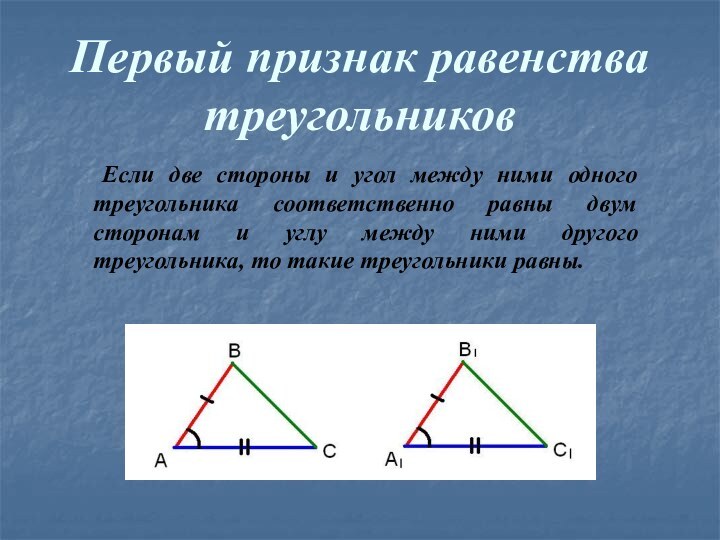
- 13. Первый признак равенства треугольников Если две стороны и
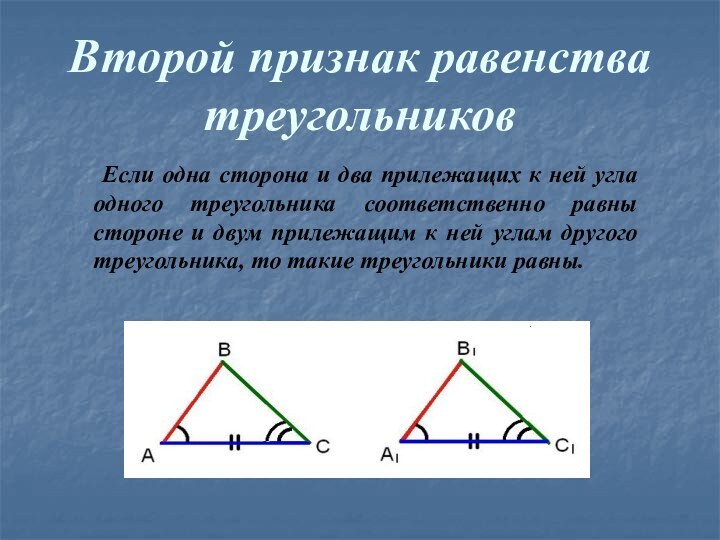
- 14. Второй признак равенства треугольников Если одна сторона и
- 15. Скачать презентацию
- 16. Похожие презентации
СодержаниеТреугольники. Определение треугольника. Виды треугольников. Медианы, биссектрисы и высоты треугольника. Признаки равенства треугольников




Слайд 2
Содержание
Треугольники.
Определение треугольника.
Виды треугольников.
Медианы, биссектрисы и
высоты треугольника.
Слайд 5
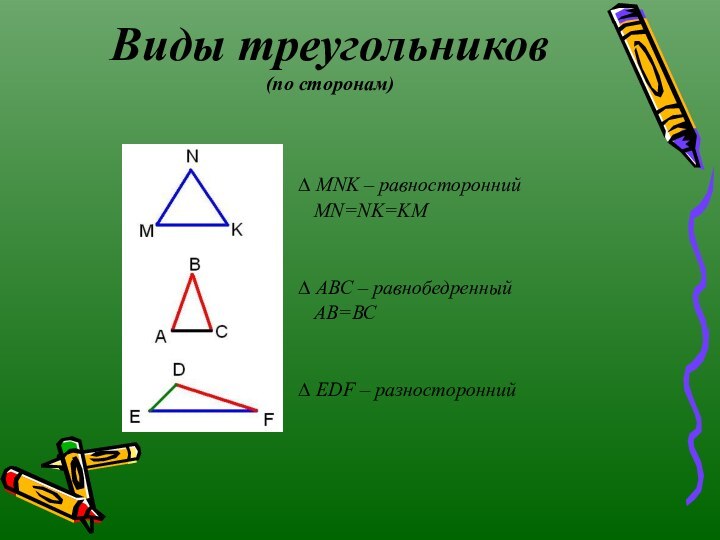
Виды треугольников
(по сторонам)
∆ MNK – равносторонний
MN=NK=KM
∆
ABC – равнобедренный
АВ=ВС
∆ EDF – разносторонний
Слайд 6
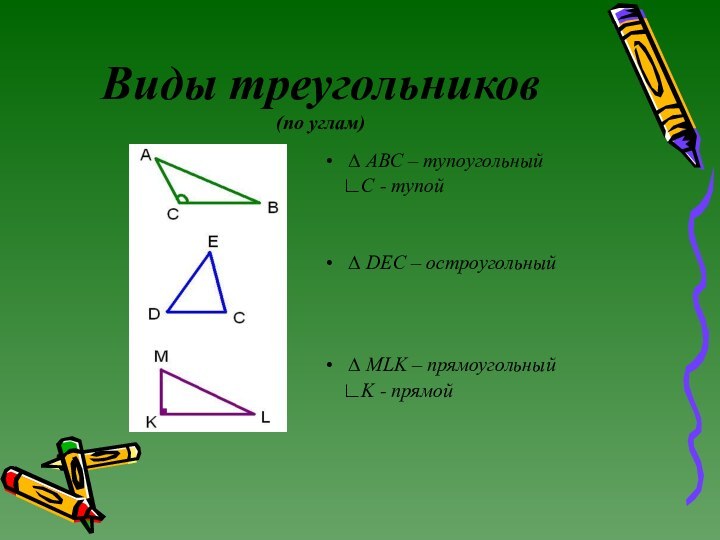
Виды треугольников
(по углам)
∆ ABC – тупоугольный
∟C
- тупой
∆ DEC – остроугольный
∆ MLK – прямоугольный
∟K - прямой
Слайд 7
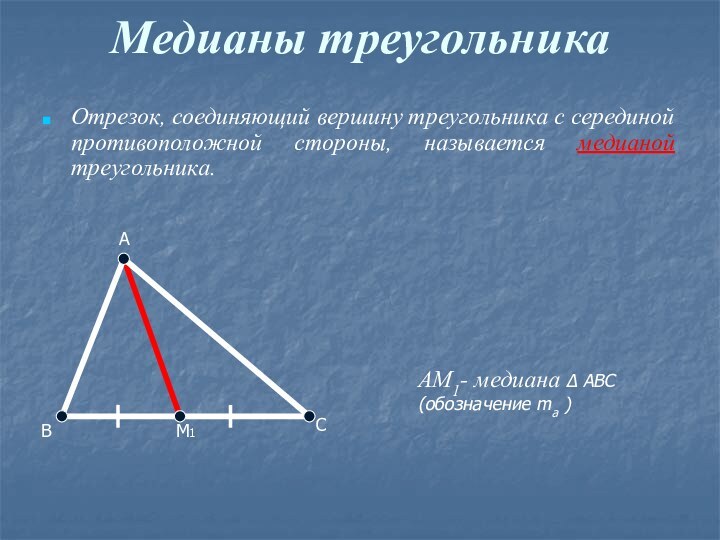
Медианы треугольника
Отрезок, соединяющий вершину треугольника с серединой противоположной
стороны, называется медианой треугольника.
AM1- медиана ∆ ABC (обозначение ma
)A
C
B
M1
Слайд 9
Биссектрисы треугольника
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника
с точкой противоположной стороны, называется биссектрисой треугольника.
AA1 -
биссектриса ∆ ABC (обозначение la) A
B
A1
C
Слайд 11
Высоты треугольника
Перпендикуляр, проведенный из вершины треугольника к прямой,
содержащий противоположенную сторону, называется высотой треугольника.
АА1 – высота ∆
ABC (обозначение ha) A
B
A1
C