для любого х из области определения функции верно равенство
f(-x) = f(x).Чтобы узнать является ли функция четной нужно в функцию f(x) вместо переменной х поставить переменную(–x).
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

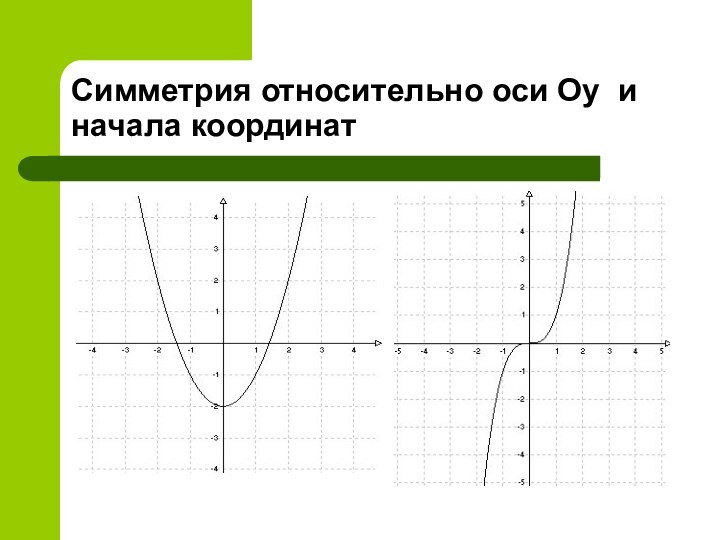



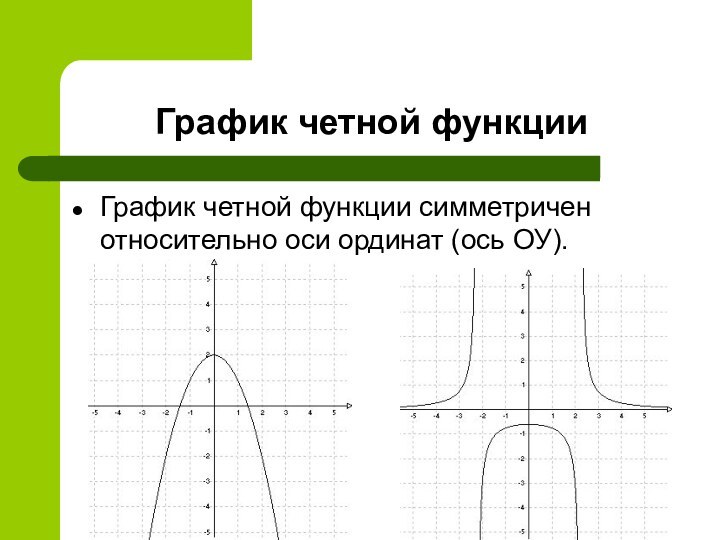



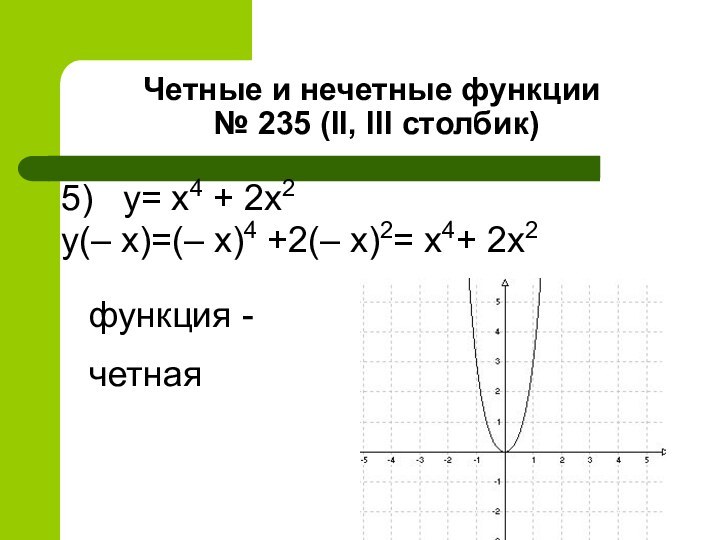



Проверим являются ли данные функции четными
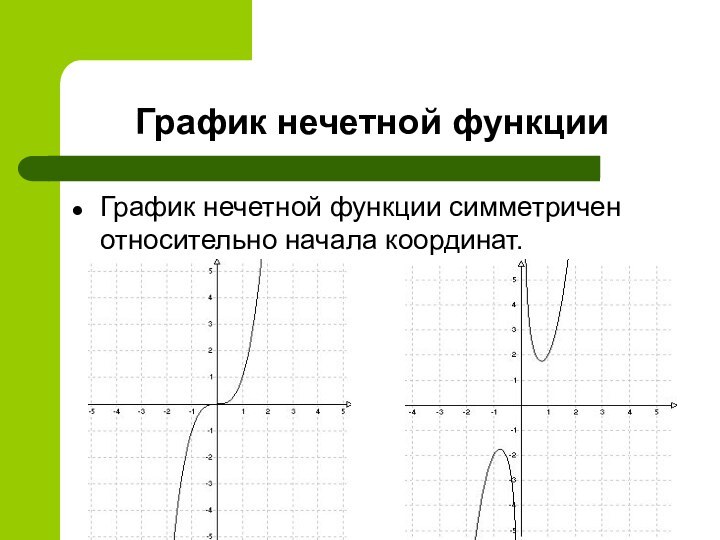
Проверим являются ли данные функции нечетными
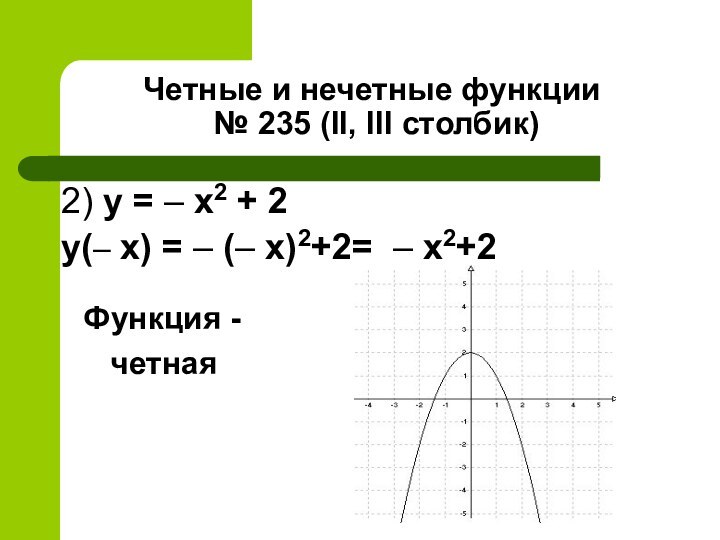
Функция -четная
функция -
четная
y(-x) = (-x)2 + 2(-x) = x2 - 2x