- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Основы логики
Содержание
- 2. Алгебра логики (булева алгебра) - это раздел
- 3. Джордж Буль
- 4. Логическое высказывание — это любое повествовательное предложение,
- 5. Так, например, предложение " Трава зеленая" следует
- 6. Не всякое предложение является логическим высказыванием.
- 7. Употребляемые в обычной речи слова и словосочетания
- 8. Bысказывания, образованные из других высказываний с помощью
- 9. Так, например, из элементарных высказываний "Петров —
- 10. При помощи связки "или" из этих же
- 11. Чтобы обращаться к логическим высказываниям, им назначают
- 12. Тогда составное высказывание "Тимур летом побывает
- 13. Операции над логическими высказываниями
- 14. НЕ Операция, выражаемая словом "не", называется
- 15. Высказывание А истинно, когда A ложно, и
- 16. И Операция, выражаемая связкой "и", называется
- 17. Высказывание А · В истинно тогда и
- 18. ИЛИ Операция, выражаемая связкой "или" (в
- 19. Высказывание А v В ложно тогда и
- 20. ЕСЛИ-ТО Операция, выражаемая связками "если
- 21. РАВНОСИЛЬНО Операция, выражаемая связками "тогда и
- 22. С помощью логических переменных и символов логических
- 23. Определение логической формулы: 1. Всякая логическая переменная
- 24. Логический элемент компьютера — это часть электронной логической схемы, которая реализует элементарную логическую функцию.
- 25. Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ и другие.
- 26. Каждый логический элемент имеет свое условное обозначение,
- 27. Таблица истинности это табличное представление логической схемы
- 28. Схема И Схема И реализует конъюнкцию двух или более логических значений.
- 29. Единица на выходе схемы И будет тогда
- 30. С х е м а ИЛИСхема ИЛИ реализует дизъюнкцию двух или более логических значений.
- 31. Таблица истинности схемы ИЛИ Когда хотя бы
- 32. С х е м а НЕСхема
- 33. Таблица истинности схемы НЕ Если на входе
- 34. С х е м а И—НЕСхема
- 35. Таблица истинности схемы И—НЕ
- 36. С х е м а ИЛИ—НЕСхема
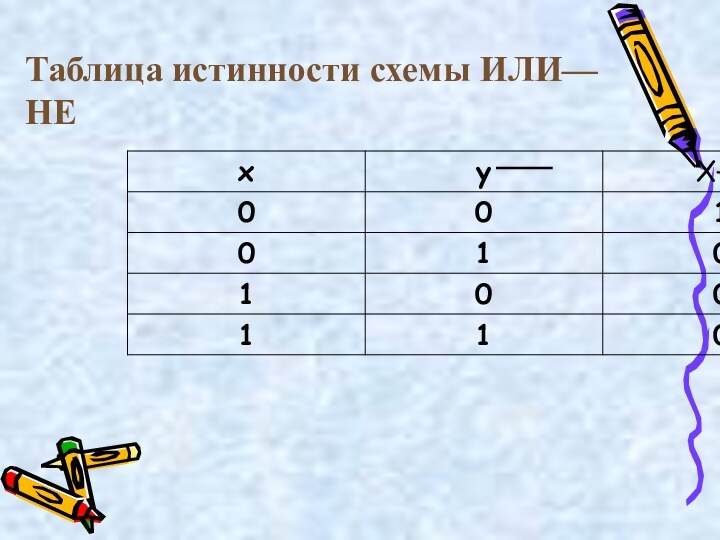
- 37. Таблица истинности схемы ИЛИ—НЕ
- 38. Триггер — это электронная схема, широко применяемая
- 39. Самый распространённый тип триггера — так называемый
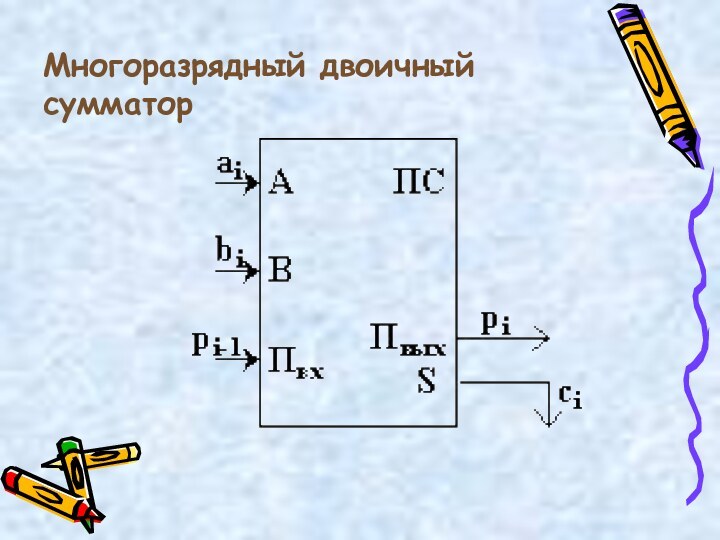
- 40. Сумматор — это электронная логическая схема, выполняющая
- 41. Скачать презентацию
- 42. Похожие презентации
Алгебра логики (булева алгебра) - это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.


































Слайд 4 Логическое высказывание — это любое повествовательное предложение, в
отношении которого можно однозначно сказать, истинно оно или ложно.
Слайд 5
Так, например, предложение
" Трава зеленая" следует считать
высказыванием, так как оно истинное.
Предложение " Лев -
птица" тоже высказывание, так как оно ложное. Слайд 6 Не всякое предложение является логическим высказыванием. Высказываниями не
являются, например, предложения "ученик десятого класса" и "информатика —
интересный предмет".Слайд 7 Употребляемые в обычной речи слова и словосочетания "не",
"и", "или", "если... , то", "тогда и только тогда"
и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками.Слайд 8 Bысказывания, образованные из других высказываний с помощью логических
связок, называются составными. Высказывания, не являющиеся составными, называются элементарными.
Слайд 9 Так, например, из элементарных высказываний "Петров — врач",
"Петров — шахматист" при помощи связки "и" можно получить
составное высказывание "Петров — врач и шахматист", понимаемое как "Петров — врач, хорошо играющий в шахматы".Слайд 10 При помощи связки "или" из этих же высказываний
можно получить составное высказывание "Петров — врач или шахматист",
понимаемое в алгебре логики как "Петров или врач, или шахматист, или и врач и шахматист одновременно".Слайд 11 Чтобы обращаться к логическим высказываниям, им назначают имена.
Пусть через А обозначено высказывание "Тимур поедет летом на
море", а через В — высказывание "Тимур летом отправится в горы". Слайд 12 Тогда составное высказывание "Тимур летом побывает и
на море, и в горах" можно кратко записать
как А и В. Здесь "и" — логическая связка, А, В — логические переменные, которые могут принимать только два значения - "истина" или "ложь", обозначаемые, соответственно, "1" и "0".
Слайд 14
НЕ
Операция, выражаемая словом "не", называется инверсией
или отрицанием и обозначается чертой над высказыванием.
Слайд 15 Высказывание А истинно, когда A ложно, и ложно,
когда A истинно.
Пример. "Луна — спутник Земли" (А);
"Луна — не спутник Земли" (А).
Слайд 16
И
Операция, выражаемая связкой "и", называется конъюнкцией
(лат. conjunctio — соединение) или логическим умножением и обозначается
точкой " . " (может также обозначаться знаками /\ или &).Слайд 17 Высказывание А · В истинно тогда и только
тогда, когда оба высказывания А и В истинны.
Например,
высказывание "10 делится на 2 и 5 больше 3" истинно, а высказывания "10 делится на 2 и 5 не больше 3", "10 не делится на 2 и 5 больше 3", "10 не делится на 2 и 5 не больше 3" — ложны.
Слайд 18
ИЛИ
Операция, выражаемая связкой "или" (в неисключающем
смысле этого слова), называется дизъюнкцией (лат. disjunctio — разделение)
или логическим сложением и обозначается знаком v (или плюсом).Слайд 19 Высказывание А v В ложно тогда и только
тогда, когда оба высказывания А и В ложны.
Например,
высказывание "10 не делится на 2 или 5 не больше 3" ложно, а высказывания "10 делится на 2 или 5 больше 3", "10 делится на 2 или 5 не больше 3", "10 не делится на 2 или 5 больше 3"— истинны.
Слайд 20
ЕСЛИ-ТО
Операция, выражаемая связками "если ...,
то", "из ... следует", "... влечет ...", называется импликацией
(лат. implico — тесно связаны) и обозначается знаком . Высказывание А В ложно тогда и только тогда, когда А истинно, а В ложно.
Слайд 21
РАВНОСИЛЬНО
Операция, выражаемая связками "тогда и только
тогда", "необходимо и достаточно", "... равносильно ...", называется эквиваленцией
или двойной импликацией и обозначается знаком или ~. Высказывание А В истинно тогда и только тогда, когда значения А и В совпадают.Слайд 22 С помощью логических переменных и символов логических операций
любое высказывание можно формализовать, то есть заменить логической формулой.
Слайд 23
Определение логической формулы:
1. Всякая логическая переменная и
символы "истина" ("1") и "ложь" ("0") - формулы.
2.
Если А и В - формулы, то А , А · В , А v В , А B , А В - формулы.
3. Никаких других формул в алгебре логики нет.
Слайд 24 Логический элемент компьютера — это часть электронной логической
схемы, которая реализует элементарную логическую функцию.
Слайд 25 Логическими элементами компьютеров являются электронные схемы И, ИЛИ,
НЕ, И—НЕ, ИЛИ—НЕ и другие.
Слайд 26 Каждый логический элемент имеет свое условное обозначение, которое
выражает его логическую функцию, но не указывает на то,
какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем.Слайд 27 Таблица истинности это табличное представление логической схемы (операции),
в котором перечислены все возможные сочетания значений истинности входных
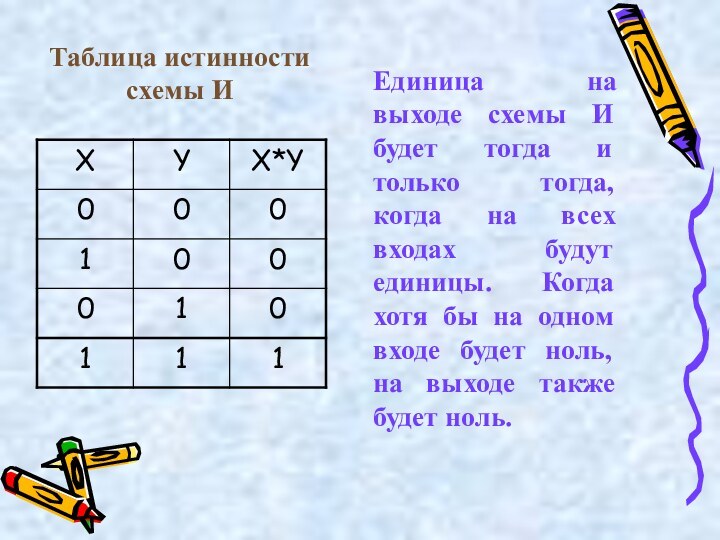
сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний.Слайд 29 Единица на выходе схемы И будет тогда и
только тогда, когда на всех входах будут единицы. Когда
хотя бы на одном входе будет ноль, на выходе также будет ноль.Таблица истинности схемы И
Слайд 31
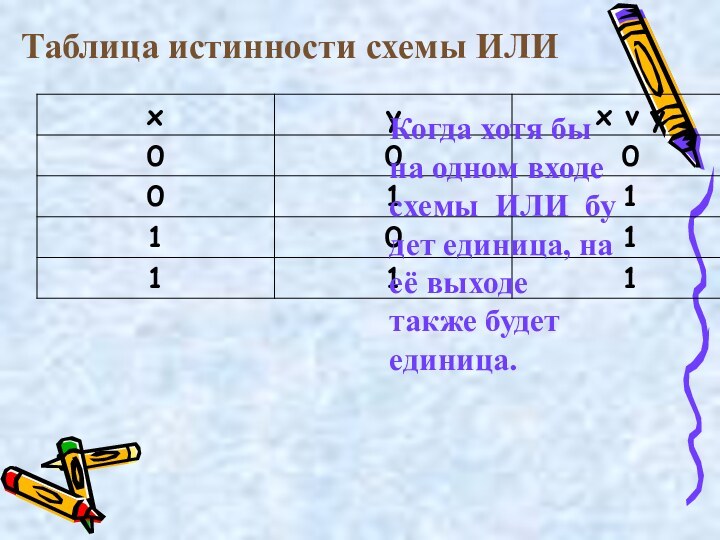
Таблица истинности схемы ИЛИ
Когда хотя бы на
одном входе схемы ИЛИ будет единица, на её выходе
также будет единица.
Слайд 32
С х е м а НЕ
Схема
НЕ (инвертор) реализует операцию отрицания. Связь между входом
x этой схемы и выходом F можно записать соотношением F = x где х читается как "не x" или "инверсия х".
Слайд 33
Таблица истинности схемы НЕ
Если на входе схемы
0, то на выходе 1. Когда на входе 1,
на выходе 0.
Слайд 34
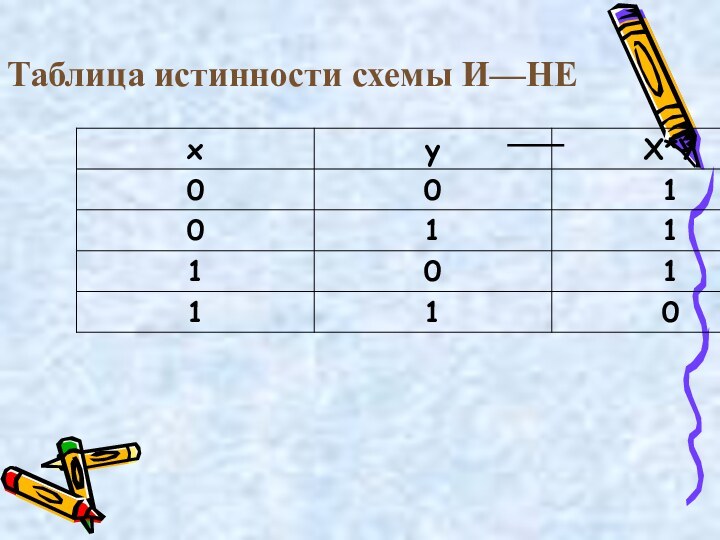
С х е м а И—НЕ
Схема И—НЕ
состоит из элемента И и инвертора и осуществляет отрицание
результата схемы И. Связь между выходом F и входами x и y схемы записывают следующим образом: F=x·y, где x·y читается как "инверсия x и y".
Слайд 36
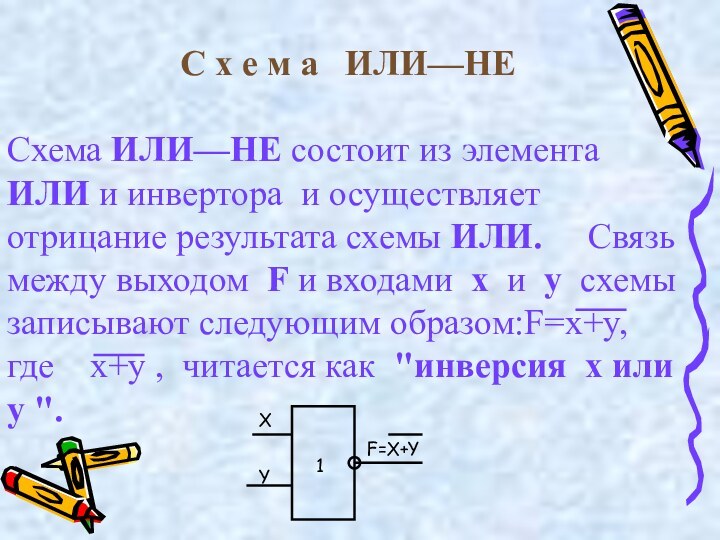
С х е м а ИЛИ—НЕ
Схема ИЛИ—НЕ
состоит из элемента ИЛИ и инвертора и осуществляет отрицание
результата схемы ИЛИ. Связь между выходом F и входами x и y схемы записывают следующим образом:F=x+y, где x+y , читается как "инверсия x или y ".
Слайд 38 Триггер — это электронная схема, широко применяемая в
регистрах компьютера для надёжного запоминания одного разряда двоичного кода.
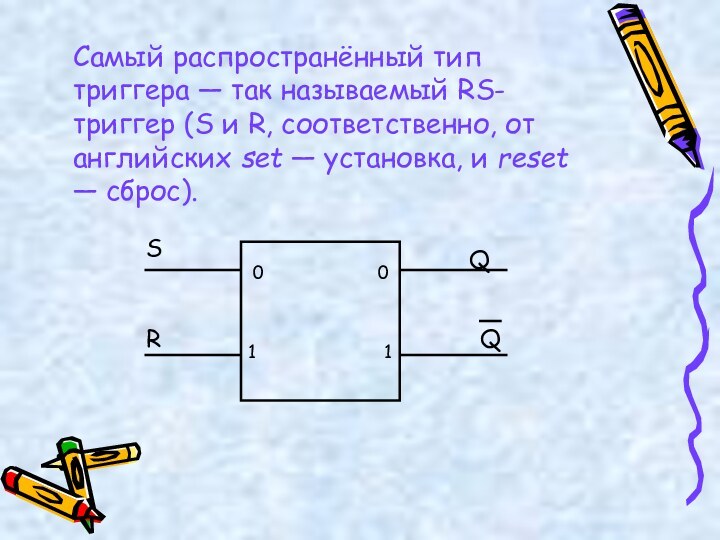
Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое — двоичному нулю.Слайд 39 Самый распространённый тип триггера — так называемый RS-триггер
(S и R, соответственно, от английских set — установка,
и reset — сброс).0
1
0
1
S
R
Q
Q





























