Презентация на тему Основы топологии

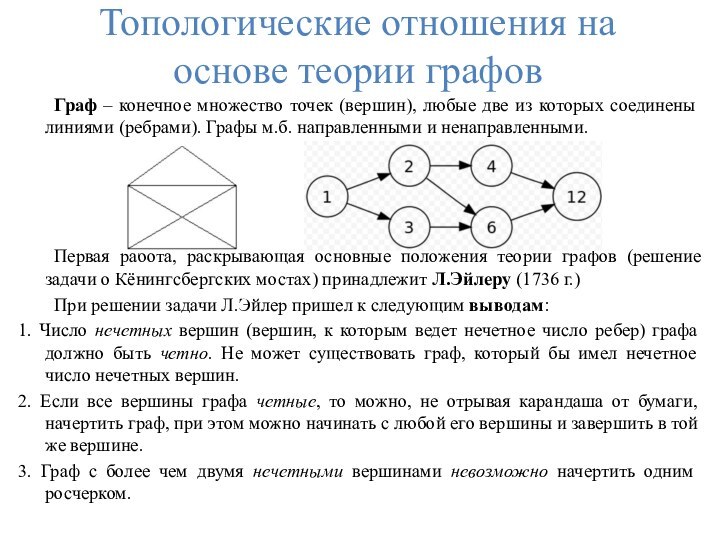
из которых соединены линиями (ребрами). Графы м.б. направленными и

ненаправленными.




Первая работа, раскрывающая основные положения теории графов (решение задачи о Кёнингсбергских мостах) принадлежит Л.Эйлеру (1736 г.)
При решении задачи Л.Эйлер пришел к следующим выводам:
1. Число нечетных вершин (вершин, к которым ведет нечетное число ребер) графа должно быть четно. Не может существовать граф, который бы имел нечетное число нечетных вершин.
2. Если все вершины графа четные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой его вершины и завершить в той же вершине.
3. Граф с более чем двумя нечетными вершинами невозможно начертить одним росчерком.

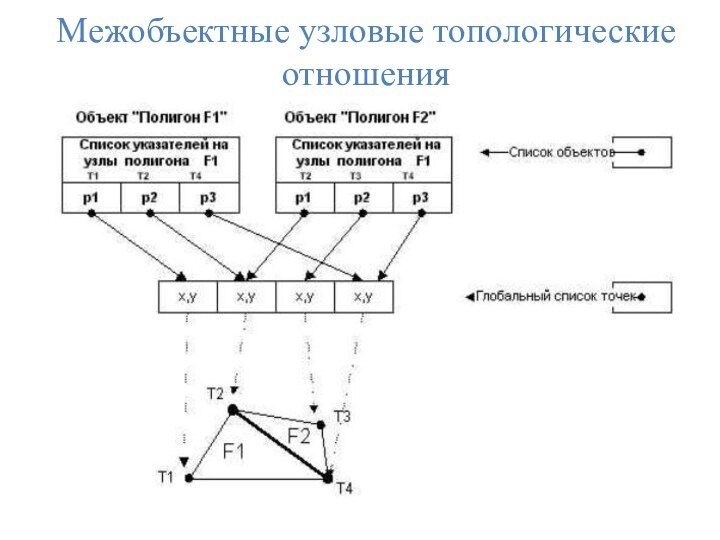
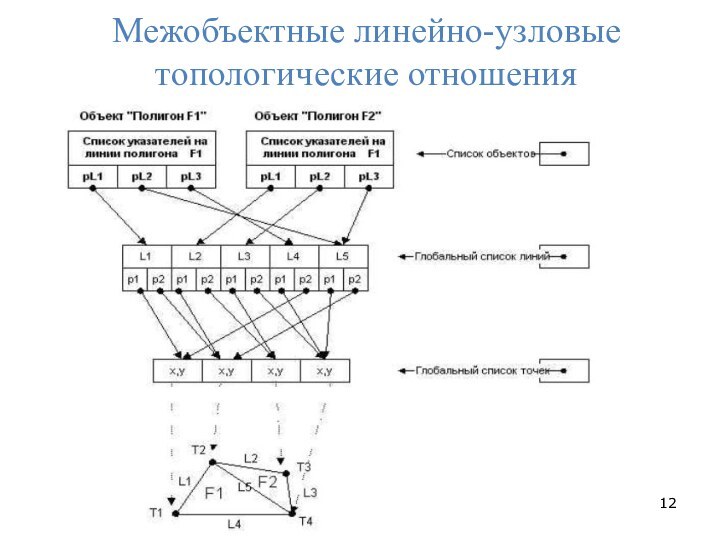
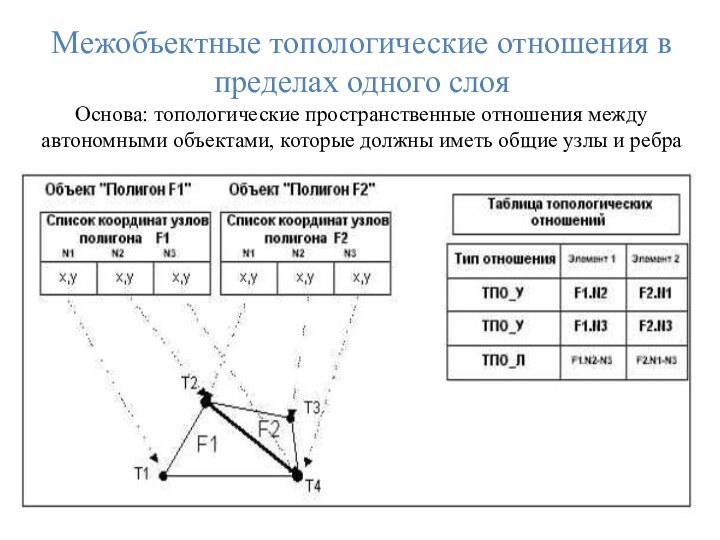
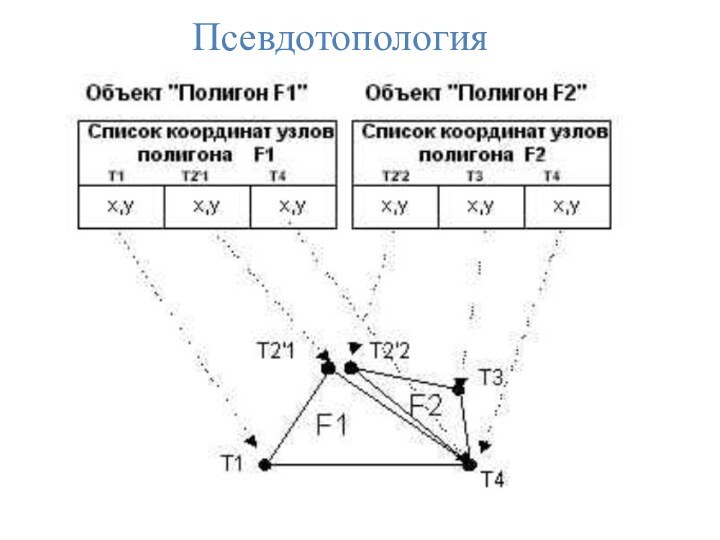
Топологические отношения на основе теории графов

соединенные отрезками (ребрами). Аналог вершины в ГИС – точка.

Ребро - соединение между вершинами графа. В ГИС синонимом термина ребро является сегмент (отрезок).
Цепь – непрерывная последовательность ребер графа.
Цепь называется простой, если все ее ребра различны, и составной — в противном случае. Если вершины цепи различны, то она называется элементарной. В ГИС синонимом цепи является ломаная (линия).
Цикл - замкнутая последовательность ребер графа.
Графы бывают двух видов: неориентированные и ориентированные (орграфы).
Ориентированный граф – граф, в котором каждому ребру, соединяющим две вершины, придана ориентация относительно этих вершин.
Дуга - фундаментальное понятие теории графов; определяется как упорядоченная пара вершин, графически изображается отрезком непрерывной кривой со стрелкой, направленной от вершины v - начала дуги к вершине w – концу дуги.

между двумя заданными вершинами.
Контур - замкнутый путь графа.

Петля - контур, образованный дугой вида (xk, xk,).
Путь называется простым, когда в нем никакая дуга не встречается дважды.
Путь, в котором никакая вершина не встречается дважды, называется элементарным. В ГИС аналогом термина путь является дуга .
Грань плоского графа - область, ограниченная ребрами графа и не содержащая внутри себя ни вершин, ни ребер (аналог в ГИС – полигон).
Край грани - цикл, образованный граничными ребрами (аналог в ГИС – контур полигона).
Смежные грани – грани, у которых края имеют хотя бы одно общее ребро.
Бесконечная грань - область плоскости, расположенная вне крайних ребер графа.

Основные элементы теории графов

в которых нет регулярных ячеек (полигонов):
1. Отношение инцидентности

(принадлежности) узла ко всем дугам, оканчивающимся на нем. Инцидентность дословно означает состояние «впадения друг в друга» или «включения друг друга» элементов графа, то есть ребро включает в себя свои начальные и конечные узлы. И напротив, все отходящие от одного узла ребра, инцидентны с ним. Инцидентность обозначает отношение между разными элементами графа.
2. Отношение инцидентности дуги к обоим ее конечным узлам.
3. Отношение адъяцентности (смежности) узла ко всем связанным с ним по краю соседним узлам. Адъяцентность означает отношение между одинаковыми элементами графа.
4. Отношение смежности дуги ко всем соседним дугам, кончающимся в том же узле (две дуги не пересекаются или пересекаются только в узлах).

1. Отношение инцидентности (принадлежности) узла ко всем граням (ячейкам,

областям, полигонам), к которым принадлежит узел.
2. Отношение инцидентности края грани (границы полигона) к двум или менее граням (полигонам), которым принадлежит край (граница). Любая дуга (вся, а не ее часть) принадлежит только одному (если она висячая) или только двум (если она невисячая) полигонам.
3. Отношение инцидентности ячейки (полигона) ко всем краям (границам полигона), которые образуют контур, определяющий ячейку.
4. Отношение адъяцентности ячейки (полигона) ко всем соседним ячейкам (полигонам), которые имеют с ячейкой, по меньшей мере, один край (топологическое свойство непрерывности).

Типологические отношения на основе теории графов

областей

топологии:
1.1. Внутриобъектные топологические отношения
1.2. Межобъектные топологические отношения:

1.2.1.Узловые топологические отношения и линейно-узловые топологические отношения
1.2.2.Межобъектные топологические отношения в пределах одного слоя
1.2.3.Межслойные топологические отношения между объектами
1.2.4. Топологические межобъектные ресурсные связи
2. Концептуальные топологические отношения (отношения между классами объектов, а не между экземплярами).
3. «Псевдотопология» (виртуальная топология)

2. Каждый тип объекта создаётся своей специфической операцией, не

допускающей изменений типа объекта,
3. С объектом можно будет выполнять только целостные операции: создать, удалить, переместить объект в другое место (не меняя формы), скопировать в другое место (не меняя формы).
К системам, которые поддерживают только внутриобъектную топологию, относятся: MapInfo (MapInfo Corp., США); AtlasGIS (ESRI, США); отечественная GeoCAD System (Новосибирск); отечественная "Панорама" for DOS (Ногинск) и т.д.

Модель в внутриобъектными топологическими отношениями

пространственные отношения между автономными объектами, которые должны иметь общие

узлы и ребра

Полезность использования КТО в ГИС состоит в следующем:

1. Появляется

возможность при реализации КТО освободить пользователя от необходимости самому следить за тем, чтобы не ввести ошибки во взаимное расположение объектов разных классов на карте. Например:
- объекты класса “здания” не должны пересекать границы объектов класса “земельные участки”;
- объекты класса “здания” не могут накладываться на объекты классов “лес” или “река”;
объекты класса “квартал” образуют топологически связанную группу с объектами классов “сегмент улицы” и “перекресток” и др.

Задание подобного рода “разрешительных” или “запретительных” отношений между классами объектов, позволяют ГИС непрерывно следить за действиями пользователя и давать ему рекомендации непосредственно в процессе создания электронной карты.

2. Реализации КТО может помочь автоматизировать процесс построения объектов некоторых классов. Например, когда границы объектов одного класса определяются через границы объектов другого класса (например, “сегменты улиц”, “перекрестки” и “кварталы”), то нарисовав слой кварталов, пользователь может дать команду для ООГИС автоматически создать слои “сегментов улиц” и “перекрестков”, поскольку они по определению размещаются между кварталами (“перекрестки” - между смежными сегментами улиц). При этом система сразу установит все необходимые топологические отношения между экземплярами этих объектов.