Презентация на тему Пирамиды

– основания пирамиды, точки, не лежащей в плоскости основания,

– вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания.
Поверхность пирамиды состоит из основания и боковых граней. Каждая боковая грань – треугольник. Одной из его вершин является вершина пирамиды, а противолежащей стороной – сторона основания пирамиды.
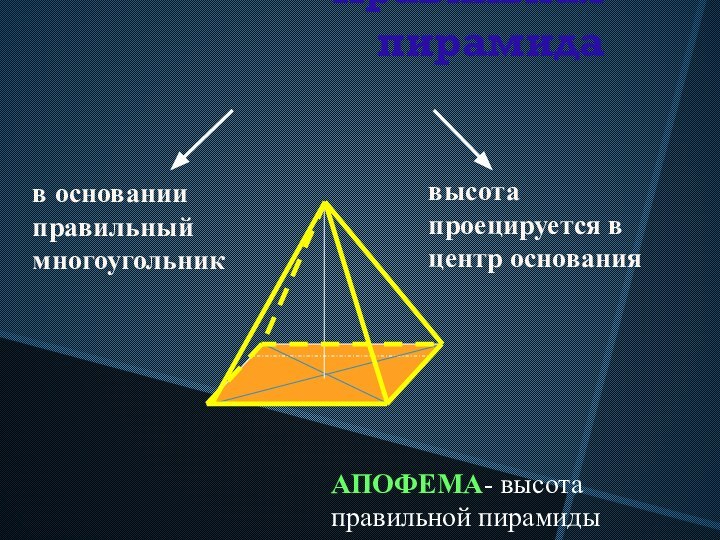
Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.

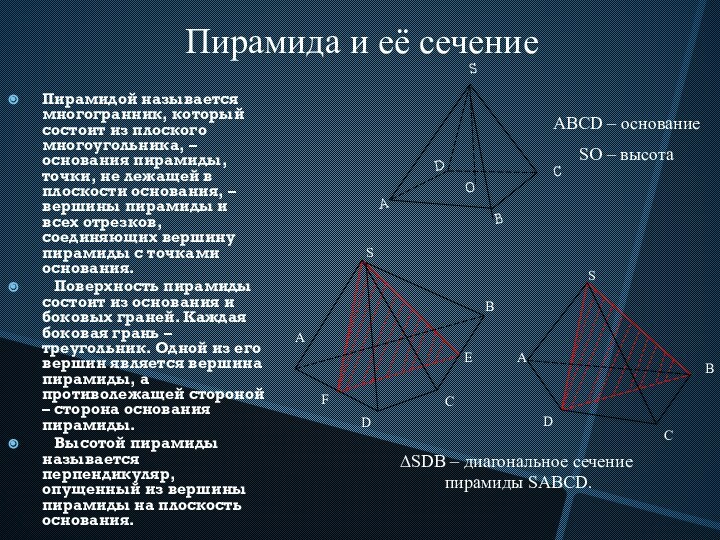
ABCD – основание
SO – высота

∆SDB – диагональное сечение
пирамиды SABCD.

Пирамида и её сечение

основания
АПОФЕМА- высота правильной пирамиды

пирамиды можно описать окружность, причём вершина пирамиды проецируется в

её центр;
боковые рёбра образуют с плоскостью основания равные углы;
также верно и обратное, то есть если боковые рёбра образуют с плоскостью основания равные углы, или если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые рёбра пирамиды равны.
Если боковые грани наклонены к плоскости основания под одним углом, то:
около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр;
высоты боковых граней равны;
площадь боковой поверхности равна половине произведения периметра основания на высоту боковой грани.

пирамиды можно описать сферу или
вписать сферу в неё.*

Конус – может быть вписанным в пирамиду или описанным вокруг неё.* Высоты у таких конусов и пирамид равны между собой.
Цилиндр – так же, как и конус, может быть вписанным в пирамиду или описанным вокруг неё.*

*при определенных условиях, описанных в соответствующих теоремах.

ограниченную плоскостями, которые от одной плоскости сходятся к одной

точке.
Герон предложил следующее определение пирамиды: «Это фигура, ограниченная треугольниками, сходящимися в одной точке и основанием которой служит многоугольник».

форму пирамиды (иногда ступенчатую или башнеобразную). Пирамидами называют гробницы

древне-египетских фараонов 3 – 2-го тыс. до н. э., а также постаменты храмов в Центральной и Южной Америке, связанные с космологическими культами.
Терра-Лексикон: Иллюстрированный
энциклопедический словарь, 1998