Презентация на тему Планиметрия. Решение прямоугольного треугольника

стороны равны.
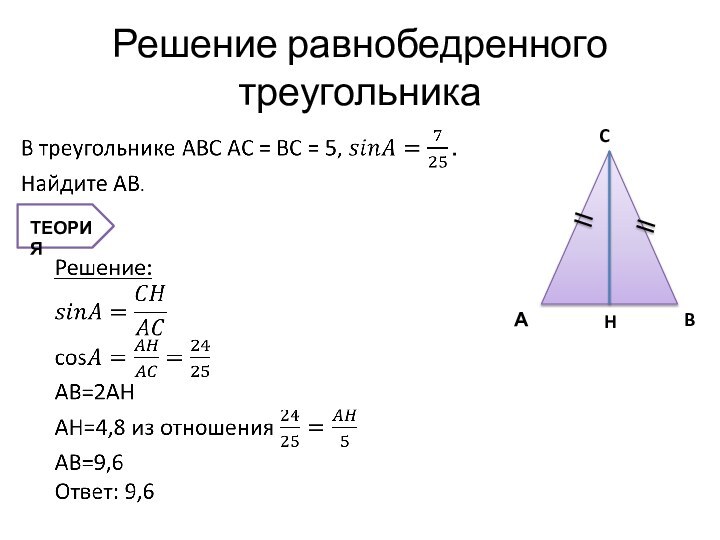
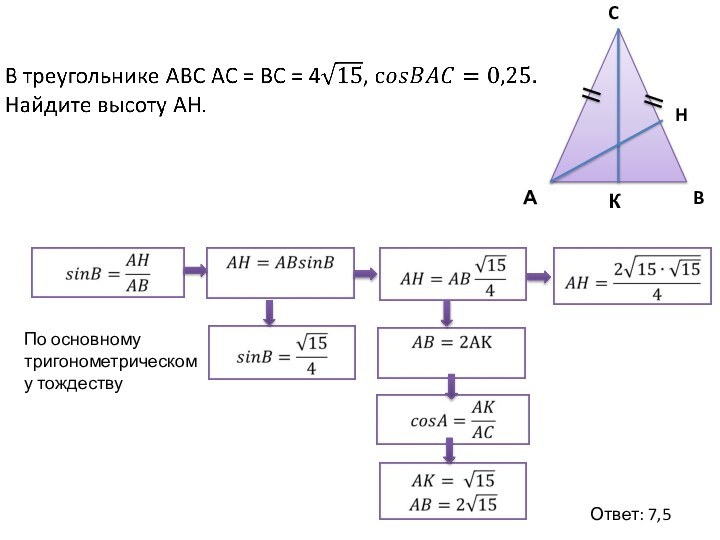
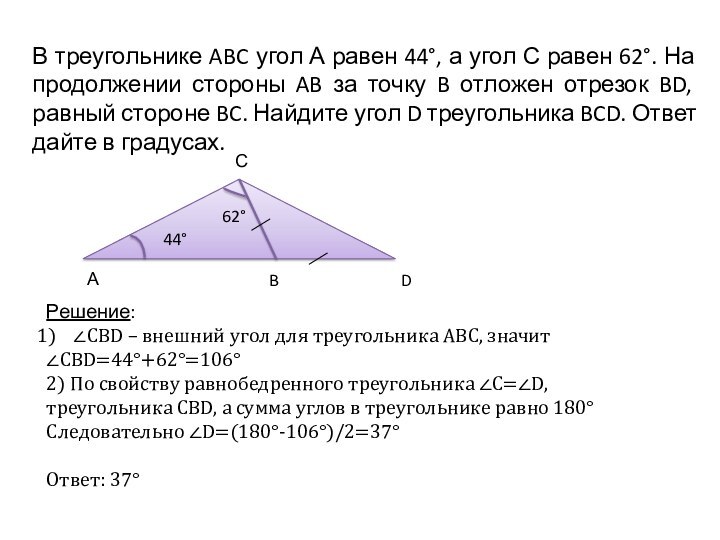
Свойства равнобедренного треугольника: Углы при основании равны

Биссектриса (делит угол пополам), проведенная к основанию, является и медианой (делит сторону пополам) и высотой (перпендикуляр).

внешний угол при вершине B равен 102°. Найдите угол

С. Ответ дайте в градусах.

А

B

C

40°

102°

 

Решение 2:
∠CBK и ∠CBA смежные, а значит в сумме дают 180°.
∠CBA=180°-102°=78°
2) Сумма углов в треугольнике равна 180°. Значит ∠С= 180°-(78°+40°)=62°

К

угол С равен 62°. На продолжении стороны AB за

точку B отложен отрезок BD, равный стороне BC. Найдите угол D треугольника BCD. Ответ дайте в градусах.

А

С

B

D

Решение:
∠CBD – внешний угол для треугольника ABC, значит
∠CBD=44°+62°=106°
2) По свойству равнобедренного треугольника ∠C=∠D, треугольника CBD, а сумма углов в треугольнике равно 180° Следовательно ∠D=(180°-106°)/2=37°

Ответ: 37°

44°

62°

прямые.
Ромб – это параллелограмм, у которого все стороны равны.
Квадрат

– это параллелограмм, у которого все углы прямые и стороны равны.
Или
Квадрат – это ромб, у которого все углы прямые.

квадрата равна половине произведения его диагоналей.

Ответ: 0,5


 

вершина которого лежит в центре окружности.
Центральный угол равен дуге,

на которую он опирается.
Вписанный угол – это угол, вершина которого лежит на окружности.
Вписанный угол равен половине дуги, на которую он опирается.
Вписанные угла, опирающиеся на одну и туже дугу, равны.
Теорема об угле, опирающемся на диаметр окружности: Угол, опирающийся на диаметр окружности – прямой.

отрезки AC и BD – диаметры. Вписанный угол ACB

равен 38°. Найдите центральный угол AOD. Ответ дайте в градусах.

Решение:

1) ∠ACB и ∠AОB – опираются на одну и туже дугу AB.
2) Дуга AB равна 38°*2= 76°, так как ∠ACB – вписанный угол, значит ∠AОB = 76°, так как он центральный угол и равен дуге, на которую он опирается.
3) ∠AОB и ∠AОD – смежные, а значит в сумме дают 180°.
∠AОD = 180°-76°=104°

Ответ: 104°

окружностью одну общую точку.
Отрезки касательных к окружности, проведенные из

одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и цент окружности.
Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
Секущая – прямая, пересекающая окружность в двух точках.
Хорда – это отрезок соединяющий точки на окружности (хорда проходящая через центр окружности называется диаметром)

касается окружности, дуга AB - равна 64°. Ответ дайте

в градусах.

Решение:

Дуга AB равна 64°, значит ∠AOС = 64°, так как является центральным углом.
Касательная к окружности перпендикулярна радиусу, проведенному в точку касания, значит треугольник AOC – прямоугольный, сумма острых углов равна 90°.
∠ACO = 90°-64°=26°

Ответ: 26