- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Бордюры
Содержание
- 2. Геометрические преобразования – тема школьного курса геометрии,
- 3. Бордюр(в геометрии) – это периодически повторяющийся рисунок на длинной ленте.
- 4. Бордюр первого типа. Этот тип бордюра получается
- 5. Бордюр второго типа. Чтобы получить бордюр этого
- 6. Бордюр третьего типа. Чтобы получить бордюр этого
- 7. Бордюр четвертого типа. В преобразовании первоначального элемента
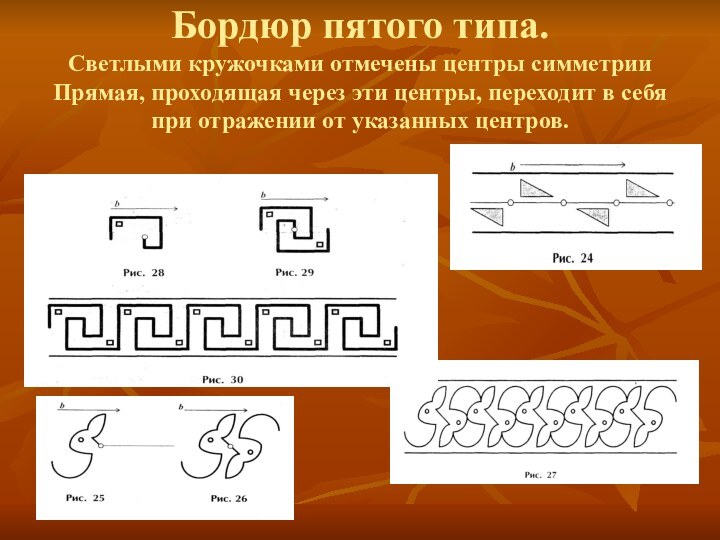
- 8. Бордюр пятого типа. Светлыми кружочками отмечены центры
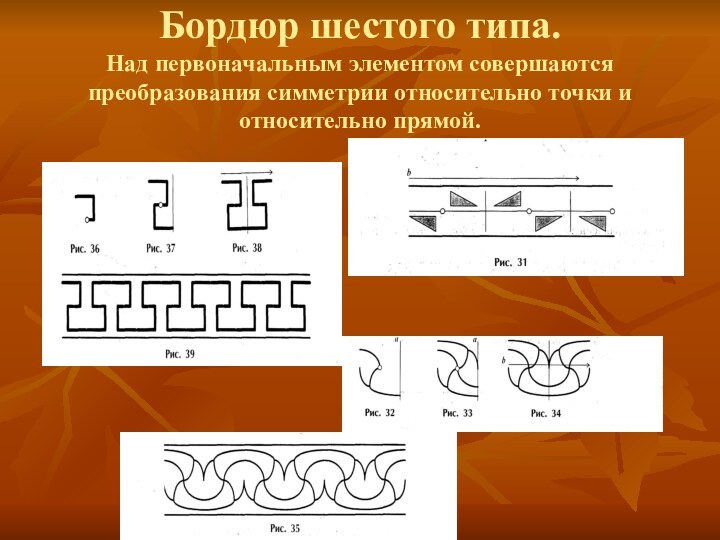
- 9. Бордюр шестого типа. Над первоначальным элементом совершаются преобразования симметрии относительно точки и относительно прямой.
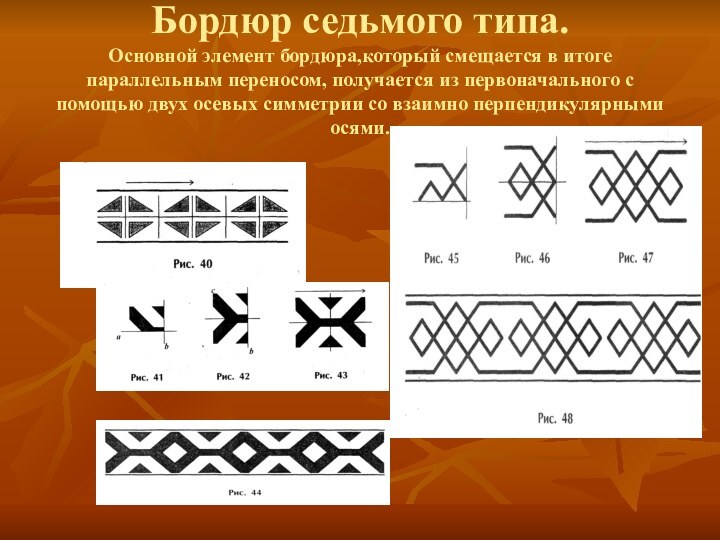
- 10. Бордюр седьмого типа. Основной элемент бордюра,который смещается
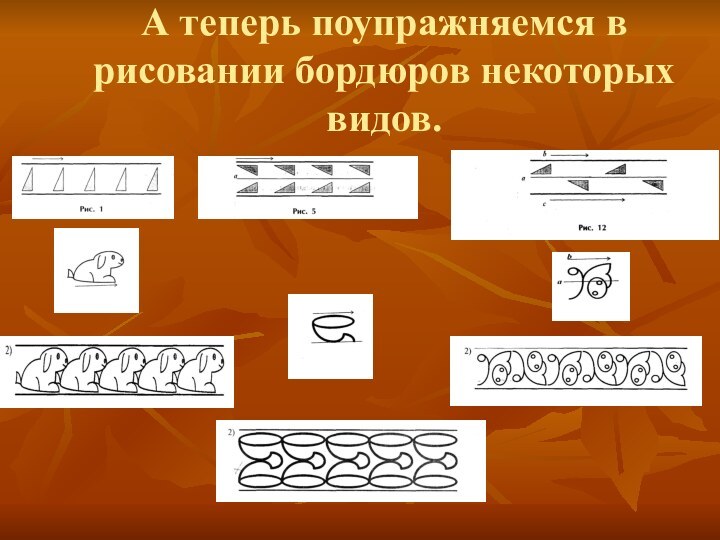
- 11. А теперь поупражняемся в рисовании бордюров некоторых видов.
- 12. Малый энциклопедический словарь Брокгауза и Ефрона.Бордюр(франц.)- 1.
- 13. Современный экономический словарь. Бордюр(франц.bordure)- проведение торговых операций за пределами официального времени работы биржи.
- 14. Бордюры в жизни.
- 19. Скачать презентацию
- 20. Похожие презентации
Геометрические преобразования – тема школьного курса геометрии, которая застывшие формы геометрических фигур позволяет сделать динамичными. Восприятие этой динамики помогает нам лучше осознавать их свойства, формирует гибкость ума.



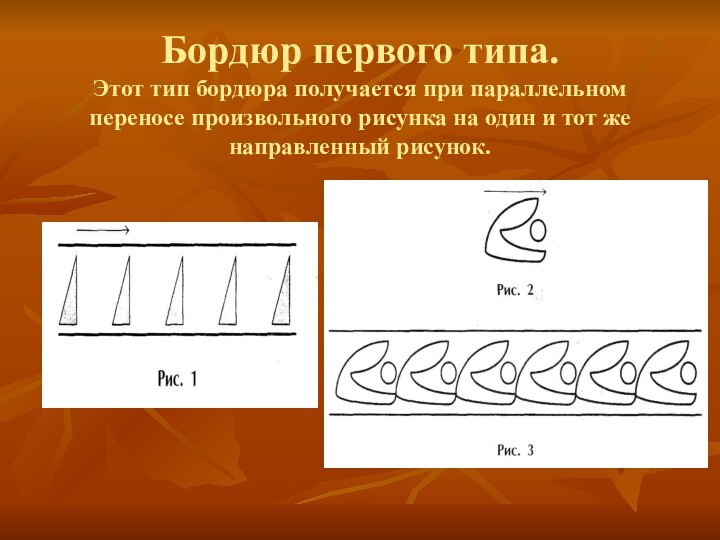








Слайд 4 Бордюр первого типа. Этот тип бордюра получается при параллельном
переносе произвольного рисунка на один и тот же направленный
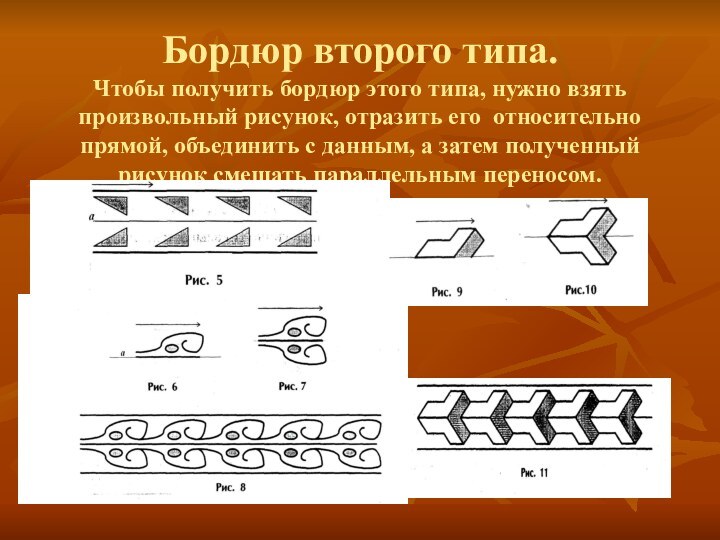
рисунок.Слайд 5 Бордюр второго типа. Чтобы получить бордюр этого типа, нужно
взять произвольный рисунок, отразить его относительно прямой, объединить с
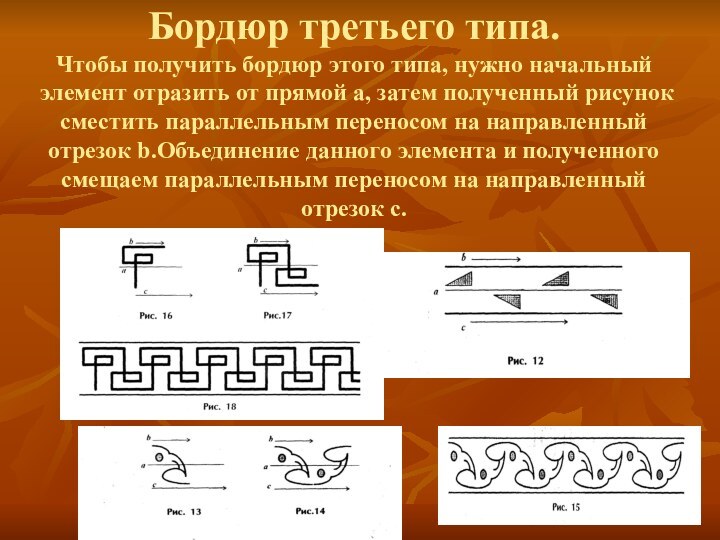
данным, а затем полученный рисунок смещать параллельным переносом.Слайд 6 Бордюр третьего типа. Чтобы получить бордюр этого типа, нужно
начальный элемент отразить от прямой а, затем полученный рисунок
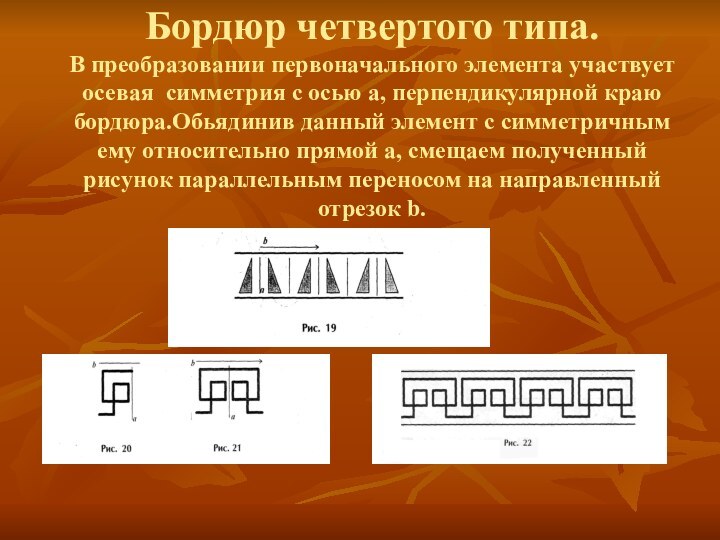
сместить параллельным переносом на направленный отрезок b.Объединение данного элемента и полученного смещаем параллельным переносом на направленный отрезок с.Слайд 7 Бордюр четвертого типа. В преобразовании первоначального элемента участвует осевая
симметрия с осью а, перпендикулярной краю бордюра.Обьядинив данный элемент
с симметричным ему относительно прямой а, смещаем полученный рисунок параллельным переносом на направленный отрезок b.Слайд 8 Бордюр пятого типа. Светлыми кружочками отмечены центры симметрии Прямая,
проходящая через эти центры, переходит в себя при отражении
от указанных центров.Слайд 9 Бордюр шестого типа. Над первоначальным элементом совершаются преобразования симметрии
относительно точки и относительно прямой.
Слайд 10 Бордюр седьмого типа. Основной элемент бордюра,который смещается в итоге
параллельным переносом, получается из первоначального с помощью двух осевых
симметрии со взаимно перпендикулярными осями.
Слайд 12
Малый энциклопедический словарь Брокгауза и Ефрона.
Бордюр(франц.)-
1. Край,кайма,кромка.
2.Цветная бумажная
лента, наклеиваемая по верху обоев. 3.Узорчатые украшения для обрамления типографского
набора на заглавных листах, бланках, афишах и пр.Слайд 13 Современный экономический словарь. Бордюр(франц.bordure)- проведение торговых операций за пределами официального
времени работы биржи.
Слайд 14
Бордюры в жизни.
Бордюры используются в
настенных росписях, в чугунном литье для оград,
мостов, набережных.
Рисунки в виде бордюров
наносятся на ткани, мебель, обои.





























