- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Подобие треугольников
Содержание
- 2. Пропорциональные отрезкиОтношением отрезков AB и CD называется
- 3. Определение подобных треугольников Два треугольника
- 4. Отношение площадей подобных треугольников Отношением площадей
- 5. Признаки подобия треугольниковI признак подобия треугольников
- 6. Признаки подобия треугольниковII признак подобия треугольников
- 7. Признаки подобия треугольниковIII признак подобия треугольников
- 8. Применение подобия к доказательству теоремСредняя линия треугольника
- 9. Применение подобия к решению задач
- 10. Применение подобия к решению задач
- 11. Применение подобия к доказательству теорем
- 12. Скачать презентацию
- 13. Похожие презентации
Пропорциональные отрезкиОтношением отрезков AB и CD называется отношение их длин, т.е. Отрезки AB и CD пропорциональны отрезкам A1B1 и C1D1, если








Слайд 2
Пропорциональные отрезки
Отношением отрезков AB и CD называется отношение
их длин, т.е.
A1B1 и C1D1, если
Слайд 3
Определение подобных треугольников
Два треугольника называются
подобными, если их углы соответственно равны и стороны одного
треугольника пропорциональны сходственным сторонам другого.Число k, равное отношению сходственных сторон треугольников, называется коэффициентом подобия
Слайд 4
Отношение площадей подобных треугольников
Отношением площадей двух
подобных треугольников равно квадрату коэффициента подобия
Биссектриса
треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
Слайд 5
Признаки подобия треугольников
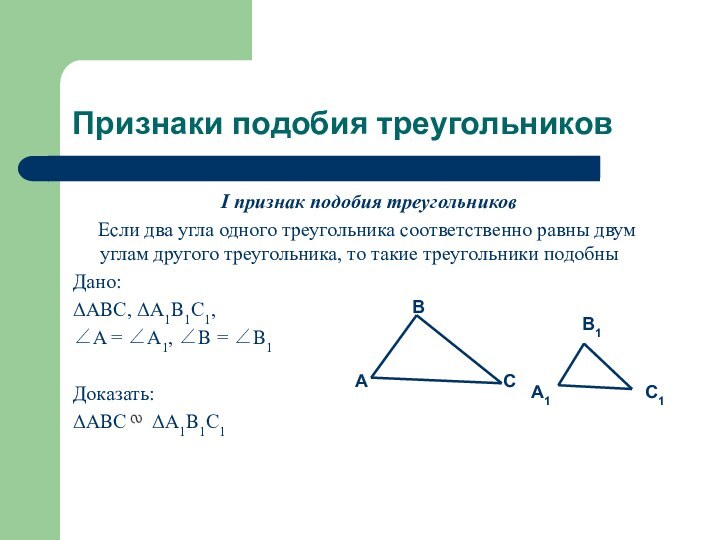
I признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам
другого треугольника, то такие треугольники подобныДано:
ABC, A1B1C1,
A = A1, B = B1
Доказать:
ABC A1B1C1
Слайд 6
Признаки подобия треугольников
II признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого
треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобныДано:
ABC, A1B1C1,
A = A1
Доказать:
ABC A1B1C1
Слайд 7
Признаки подобия треугольников
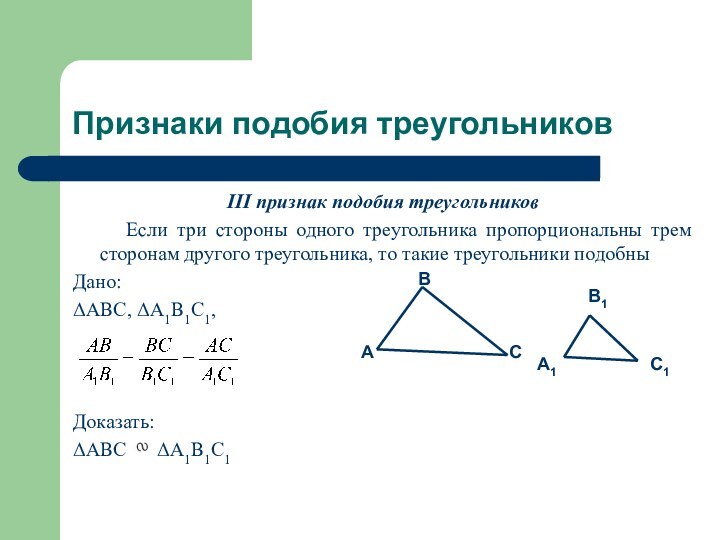
III признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого
треугольника, то такие треугольники подобныДано:
ABC, A1B1C1,
Доказать:
ABC A1B1C1
Слайд 8
Применение подобия к доказательству теорем
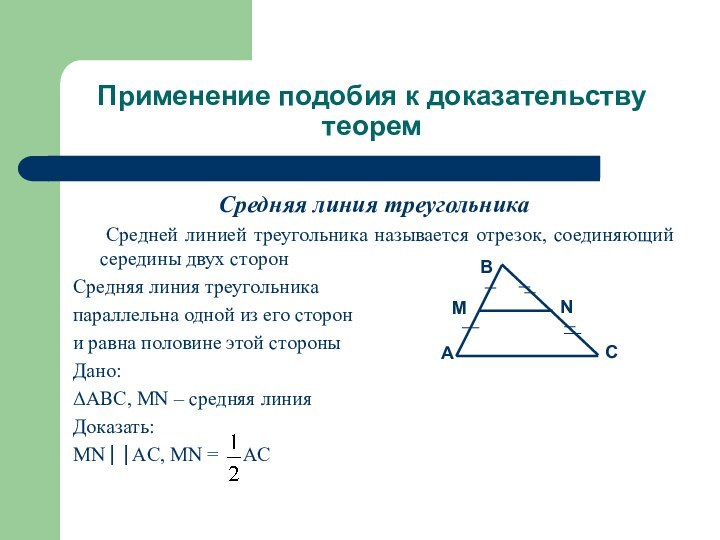
Средняя линия треугольника
Средней линией треугольника называется отрезок, соединяющий середины двух
сторонСредняя линия треугольника
параллельна одной из его сторон
и равна половине этой стороны
Дано:
ABC, MN – средняя линия
Доказать:
MNAC, MN = AC
Слайд 9
Применение подобия к решению задач
Медианы
треугольника пересекаются в одной точке, которая делит каждую медиану
в отношении 2 : 1,считая от вершины
Слайд 10
Применение подобия к решению задач
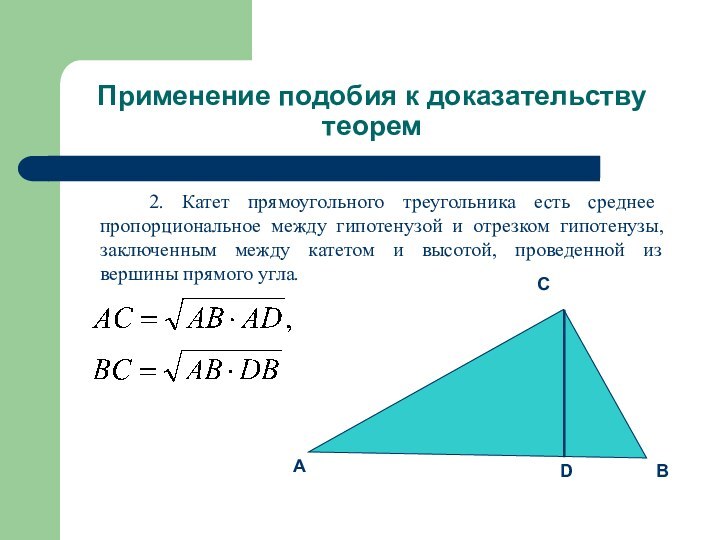
Высота
прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник
на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.ABC ACD,
ABC CBD
ACD CBD





























