Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Поверхности второго порядка

Содержание

Лекция 92. Исследование формы поверхностей второго порядка по их каноническим уравнениям.1. Основные понятия.Поверхности второго порядка.
Курс высшей математикиУГТУ-УПИ2004г. Лекция 92. Исследование формы поверхностей второго порядка по их каноническим уравнениям.1. Основные понятия.Поверхности второго порядка. F(x,y,z) = 0, Алгебраической поверхностью второго порядка называется поверхность , уравнение которой в декартовой системе Всякое уравнение (2), задающее невырожденную поверхность , путем преобразования координат можно Исследование формы поверхностей второгопорядка по их каноническим уравнениям.Основным методом исследования формы поверхности 2.1 Эллипсоид. Эллипсоидом называется поверхность второго порядка с каноническим уравнением: илиИССЛЕДОВАНИЕ ФОРМЫ ЭЛИПСОИДА МЕТОДОМ СЕЧЕНИЙ. или Точно также рассматриваются сечения эллипсоида другими плоскостями: Выполненное исследование завершается построением чертежа: 2.2 Гиперболоиды. 2.2.1 Однополостный гиперболоид.Однополостным гиперболоидом называется поверхность второго порядка с каноническим уравнением: определяющей эллипс с полуосями а и b. ИССЛЕДОВАНИЕ ФОРМЫ ОДНОПОЛОСТНОГО ГИПЕРБОЛОИДА МЕТОДОМ СЕЧЕНИЙ. В сечении плоскостью имеем кривуюявляющуюся также эллипсом с полуосями задаёт гиперболу, пересекающую ось OY. Уравнение линии пересечения 2.2.2 Двухполостный гиперболоид.Двухполостным гиперболоидом называется поверхность второго порядка с каноническим уравнением: где Если – с < h < c - нет точек задает гиперболу, пересекающую ось OZ. Итоговый чертеж представлен на рисунке: 2.3 Конус. Конусом второго порядка называется поверхность с каноническим уравнением ЗамечаниеОсью конуса, заданного рассматриваемым каноническим уравнением, является ось OZ. Продольные сечения являются 2.4 Параболоиды. 2.4.1 Эллиптический параболоид.Эллиптическим параболоидом называется поверхность с каноническим уравнением:Его Эллиптический параболоид 2.4.2 Гиперболический параболоид.Гиперболическим параболоидом называется поверхность с каноническим уравнением: Отсюда и название исследуемой поверхности, форма которой представлена на рисунке: ИССЛЕДОВАНИЕ ФОРМЫ ГИПЕРБОЛИЧЕСКОГО ПАРАБОЛОИДА МЕТОДОМ СЕЧЕНИЙ. Гиперболический параболоид Гиперболический параболоид Гиперболический параболоид 2.5 Цилиндры второго порядка . 2.5.1 Эллиптический цилиндр. 2.5.2 Гиперболический цилиндр.Гиперболический цилиндр задается каноническим уравнением: Его форма представлена на рисунке: Гиперболический цилиндр 2.5.2 Параболический цилиндр.Параболический цилиндр задается каноническим уравнением:Его форма представлена на рисунке: Параболический цилиндр Замечание:Признаком рассмотренных цилиндрических поверхностей является отсутствие одной из переменных в каноническом уравнении.
Слайды презентации

Слайд 2 Лекция 9
2. Исследование формы поверхностей второго
порядка

Лекция 92. Исследование формы поверхностей второго порядка по их каноническим уравнениям.1. Основные понятия.Поверхности второго порядка.

по их каноническим уравнениям.
1. Основные понятия.
Поверхности второго порядка.

Слайд 3 F(x,y,z) = 0,

F(x,y,z) = 0, (1)которому удовлетворяют координаты

(1)
которому удовлетворяют координаты каждой точки,

принадлежащей поверхности, и не удовлетворяют координаты ни одной точки, не принадлежащей поверхности.

Уравнением поверхности называется уравнение с тремя переменными

Слайд 4 Алгебраической поверхностью второго порядка называется поверхность , уравнение

Алгебраической поверхностью второго порядка называется поверхность , уравнение которой в декартовой

которой в декартовой системе координат имеет вид
Ax2+By2+Cz2+2Dxy+2Exz+
2Fyz+Gx+Hy+Iz+K=0, (2)
где

не все коэффициенты при слагаемых второго порядка (A,B,C,D,E,F) равны одновременно нулю.

Слайд 5 Всякое уравнение (2), задающее невырожденную поверхность , путем

Всякое уравнение (2), задающее невырожденную поверхность , путем преобразования координат можно

преобразования координат можно привести к каноническому виду

( при котором в уравнении поверхности отсутствуют слагаемые,содержащие смешанные произведения координат xy, xz, yz ).

Слайд 6 Исследование формы поверхностей второго
порядка по их каноническим уравнениям.
Основным

Исследование формы поверхностей второгопорядка по их каноническим уравнениям.Основным методом исследования формы

методом исследования формы поверхности по её уравнению является метод

сечений, когда о форме поверхности судят по форме кривых, которые получаются при пересечении данной поверхности плоскостями, параллельными координатным плоскостям :

Слайд 7 2.1 Эллипсоид.
Эллипсоидом называется поверхность второго

2.1 Эллипсоид. Эллипсоидом называется поверхность второго порядка с каноническим уравнением:

порядка с каноническим уравнением:

Слайд 8
или

ИССЛЕДОВАНИЕ ФОРМЫ ЭЛИПСОИДА МЕТОДОМ СЕЧЕНИЙ.

илиИССЛЕДОВАНИЕ ФОРМЫ ЭЛИПСОИДА МЕТОДОМ СЕЧЕНИЙ.

Слайд 9 или

или

Слайд 10


Слайд 11 Точно также рассматриваются сечения эллипсоида другими плоскостями:
Выполненное

Точно также рассматриваются сечения эллипсоида другими плоскостями: Выполненное исследование завершается построением чертежа:

исследование завершается построением
чертежа:

Слайд 12

Слайд 13 2.2 Гиперболоиды.
2.2.1 Однополостный гиперболоид.
Однополостным гиперболоидом называется

2.2 Гиперболоиды. 2.2.1 Однополостный гиперболоид.Однополостным гиперболоидом называется поверхность второго порядка с каноническим уравнением:

поверхность второго порядка с каноническим уравнением:

Слайд 14

определяющей эллипс с полуосями а и b.
ИССЛЕДОВАНИЕ

определяющей эллипс с полуосями а и b. ИССЛЕДОВАНИЕ ФОРМЫ ОДНОПОЛОСТНОГО ГИПЕРБОЛОИДА МЕТОДОМ СЕЧЕНИЙ.

ФОРМЫ ОДНОПОЛОСТНОГО ГИПЕРБОЛОИДА МЕТОДОМ СЕЧЕНИЙ.

Слайд 15
В сечении плоскостью

В сечении плоскостью имеем кривуюявляющуюся также эллипсом с полуосями

имеем кривую
являющуюся также эллипсом с полуосями

Слайд 16 задаёт гиперболу, пересекающую ось OY.

Уравнение линии пересечения

задаёт гиперболу, пересекающую ось OY. Уравнение линии пересечения

Слайд 17

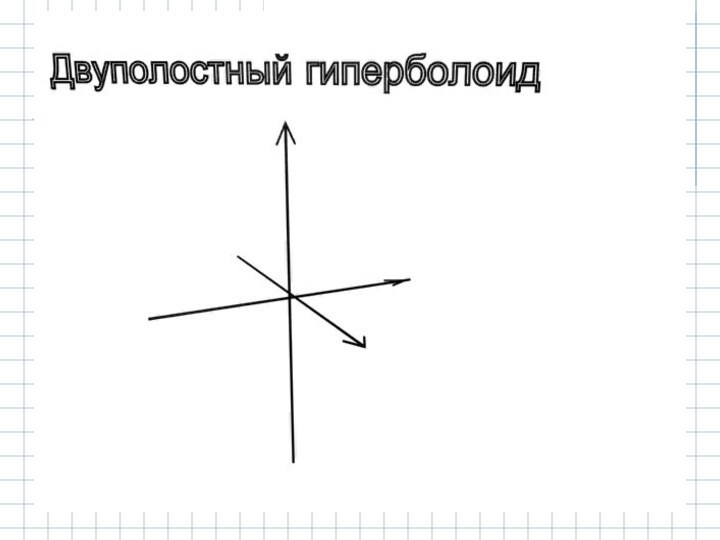
Слайд 18 2.2.2 Двухполостный гиперболоид.
Двухполостным гиперболоидом называется поверхность второго

2.2.2 Двухполостный гиперболоид.Двухполостным гиперболоидом называется поверхность второго порядка с каноническим уравнением:

порядка с каноническим уравнением:

Слайд 19
где



Если – с < h < c

где Если – с < h < c - нет точек

- нет точек пересечения.
ИССЛЕДОВАНИЕ ФОРМЫ ДВУХПОЛОСТНОГО ГИПЕРБОЛОИДА МЕТОДОМ

СЕЧЕНИЙ.

Слайд 20

задает гиперболу, пересекающую ось OZ.

Итоговый чертеж представлен

задает гиперболу, пересекающую ось OZ. Итоговый чертеж представлен на рисунке:

на рисунке:

Слайд 21

Слайд 22 2.3 Конус.
Конусом второго порядка называется

2.3 Конус. Конусом второго порядка называется поверхность с каноническим уравнением

поверхность с каноническим уравнением

Слайд 23

Слайд 24 Замечание
Осью конуса, заданного рассматриваемым каноническим уравнением, является ось

ЗамечаниеОсью конуса, заданного рассматриваемым каноническим уравнением, является ось OZ. Продольные сечения

OZ.
Продольные сечения являются прямыми линиями, поперечные сечения –

эллипсы.

Слайд 25 2.4 Параболоиды.
2.4.1 Эллиптический параболоид.
Эллиптическим параболоидом называется

2.4 Параболоиды. 2.4.1 Эллиптический параболоид.Эллиптическим параболоидом называется поверхность с каноническим

поверхность с каноническим уравнением:
Его форма показана на рисунке:

Слайд 26 Эллиптический параболоид

Эллиптический параболоид

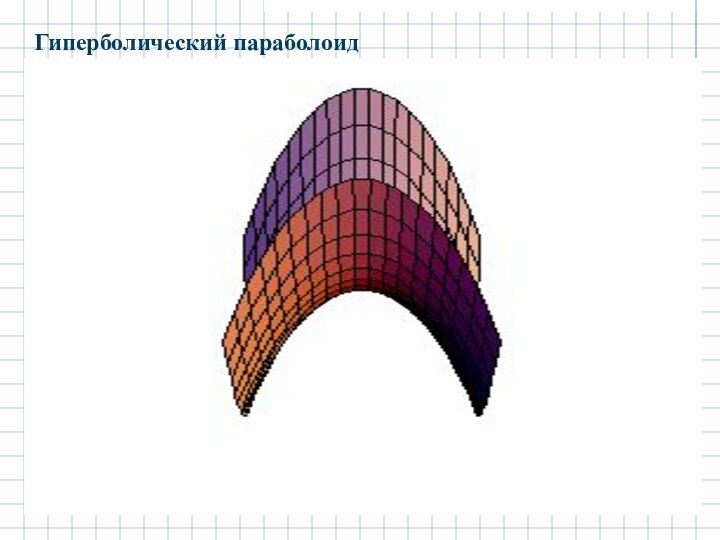
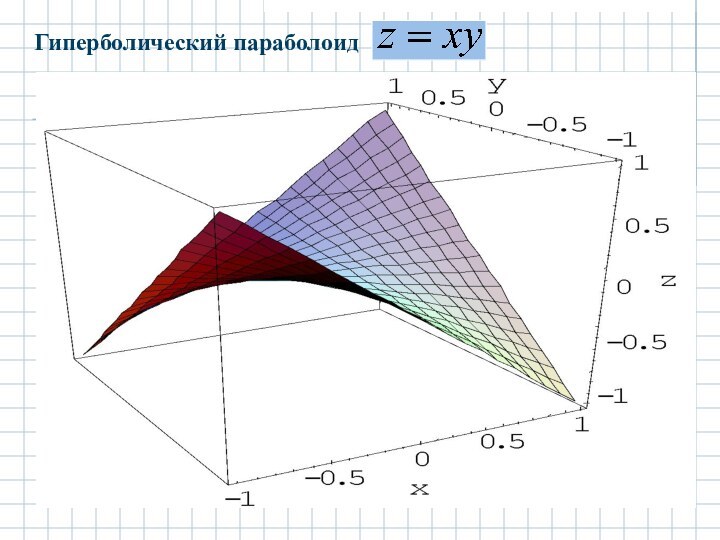
Слайд 27 2.4.2 Гиперболический параболоид.
Гиперболическим параболоидом называется поверхность с

2.4.2 Гиперболический параболоид.Гиперболическим параболоидом называется поверхность с каноническим уравнением:

каноническим уравнением:

Слайд 28
Отсюда и название исследуемой поверхности, форма которой представлена

Отсюда и название исследуемой поверхности, форма которой представлена на рисунке: ИССЛЕДОВАНИЕ ФОРМЫ ГИПЕРБОЛИЧЕСКОГО ПАРАБОЛОИДА МЕТОДОМ СЕЧЕНИЙ.

на рисунке:
ИССЛЕДОВАНИЕ ФОРМЫ ГИПЕРБОЛИЧЕСКОГО ПАРАБОЛОИДА МЕТОДОМ СЕЧЕНИЙ.


Слайд 29 Гиперболический параболоид

Гиперболический параболоид

Слайд 30 Гиперболический параболоид

Гиперболический параболоид

Слайд 31 Гиперболический параболоид

Гиперболический параболоид

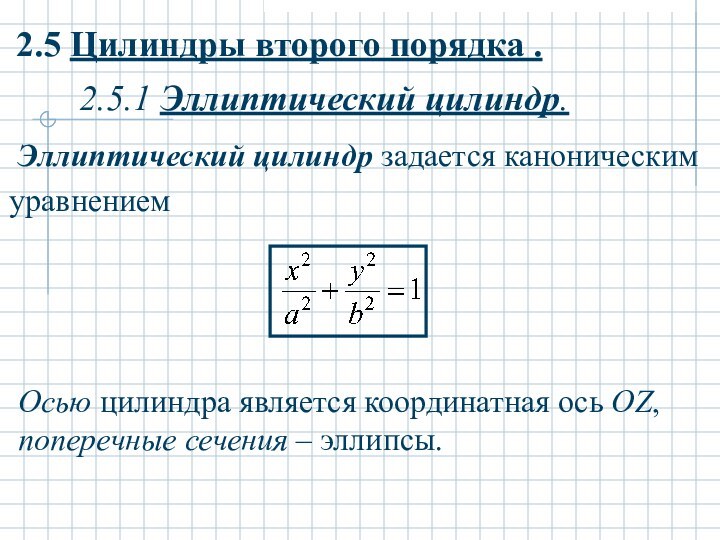
Слайд 32 2.5 Цилиндры второго порядка .

2.5 Цилиндры второго порядка . 2.5.1 Эллиптический цилиндр. Эллиптический

2.5.1 Эллиптический цилиндр.
Эллиптический цилиндр задается каноническим

уравнением

Осью цилиндра является координатная ось OZ, поперечные сечения – эллипсы.


Слайд 33

Слайд 34 2.5.2 Гиперболический цилиндр.
Гиперболический цилиндр задается каноническим уравнением:

2.5.2 Гиперболический цилиндр.Гиперболический цилиндр задается каноническим уравнением: Его форма представлена на рисунке:



Его форма представлена на рисунке:

Слайд 35 Гиперболический цилиндр

Гиперболический цилиндр

Слайд 36 2.5.2 Параболический цилиндр.
Параболический цилиндр

2.5.2 Параболический цилиндр.Параболический цилиндр задается каноническим уравнением:Его форма представлена на рисунке:

задается каноническим уравнением:

Его форма представлена на рисунке:

Слайд 37 Параболический цилиндр

Параболический цилиндр
  • Имя файла: poverhnosti-vtorogo-poryadka.pptx
  • Количество просмотров: 120
  • Количество скачиваний: 0
- Предыдущая Туберкулез мочевыделительной системы
Следующая - Растения семейства розоцветные

Похожие презентации

Презентация по математике на тему: Письменное умножение на трёхзначное число (4 класс) Презентация по математике на тему: Письменное умножение на трёхзначное число (4 класс) 121
Движение. Параллельный перенос Движение. Параллельный перенос 160
презентация к проекту к урокам математике 4 класс по теме математика вокруг нас презентация к уроку по математике (4 класс) презентация к проекту к урокам математике 4 класс по теме математика вокруг нас презентация к уроку по математике (4 класс) 133
Проектная деятельность на уроках математики Проектная деятельность на уроках математики 128
Сложение и вычитание в пределах 10 Сложение и вычитание в пределах 10 93
Методика исследования функций и построение их графиков Методика исследования функций и построение их графиков 116
Площади и объёмы Площади и объёмы 98
Методическая разработка по теме: Развитие ориентировки в пространстве у старших дошкольников. Дидактическая игра Геометрические фигуры-шаблоны. презентация к уроку по математике (старшая группа) Методическая разработка по теме: Развитие ориентировки в пространстве у старших дошкольников. Дидактическая игра Геометрические фигуры-шаблоны. презентация к уроку по математике (старшая группа) 136
Действия с натуральными числами. Площади Действия с натуральными числами. Площади 103
Презентация по математике 4 класс 2 четверть по теме:нахождение нескольких долей от целого Презентация по математике 4 класс 2 четверть по теме:нахождение нескольких долей от целого 95
Презентация Повторяем таблицу умножения. Интерактивный тренажёр Презентация Повторяем таблицу умножения. Интерактивный тренажёр 125
Математическая статистика результатов ЕГЭ Математическая статистика результатов ЕГЭ 131
Путешествие в мир математики Путешествие в мир математики 109
Непрерывность функции Непрерывность функции 119
Презентация. Урок по математикеТабличное умножение и деление. Закрепление. 2 класс презентация к уроку по математике (2 класс) Презентация. Урок по математикеТабличное умножение и деление. Закрепление. 2 класс презентация к уроку по математике (2 класс) 124
Презентация к серии уроков по геометрии Признаки равенства треугольников Презентация к серии уроков по геометрии Признаки равенства треугольников 128
Конспект занятия Зайка путешественник 2-3 года материал по математике (младшая группа) Конспект занятия Зайка путешественник 2-3 года материал по математике (младшая группа) 100
Урок по математике Числа 6,7. Письмо цифры 7 план-конспект урока по математике (1 класс) Урок по математике Числа 6,7. Письмо цифры 7 план-конспект урока по математике (1 класс) 97
Презентация Занятия удмуртов и скотоводство Презентация Занятия удмуртов и скотоводство 132
Путешествие в страну натуральных чисел Путешествие в страну натуральных чисел 100
Прямоугольник презентация к уроку по математике (2 класс) Прямоугольник презентация к уроку по математике (2 класс) 141
Викторина В гостях у Математики план-конспект урока по математике (1 класс) Викторина В гостях у Математики план-конспект урока по математике (1 класс) 98
Площадь фигур презентация к уроку по математике (2 класс) Площадь фигур презентация к уроку по математике (2 класс) 103
Сложение и вычитание рациональных чисел Сложение и вычитание рациональных чисел 128
Арифметические действия Арифметические действия 91
Веселая математика Веселая математика 123
Презентация открытого урока Выражение отношения в процентах Презентация открытого урока Выражение отношения в процентах 139
Показательная функция ее свойства и график Показательная функция ее свойства и график 98
Объемы. Объем прямоугольного параллелепипеда Объемы. Объем прямоугольного параллелепипеда 124
Взаимосвязь действий сложения и вычитания Взаимосвязь действий сложения и вычитания 121