Презентация на тему Правильные многогранники. Часть 1 - Платоновы тела

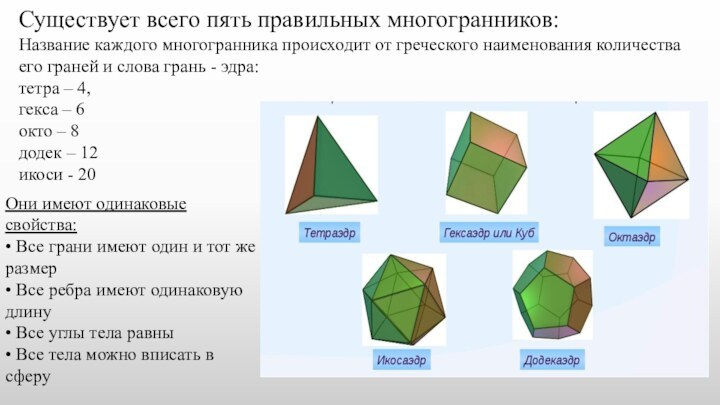
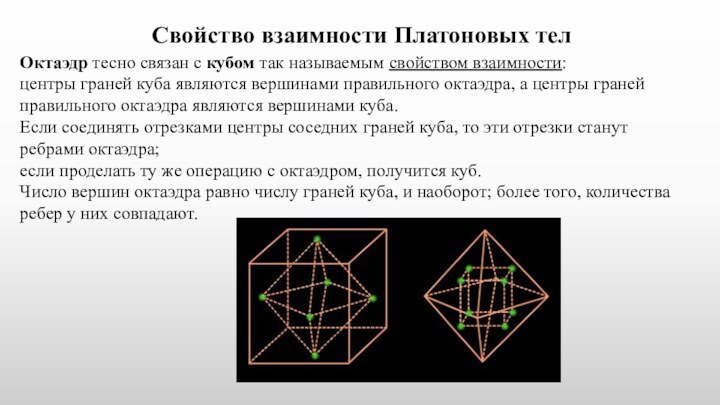
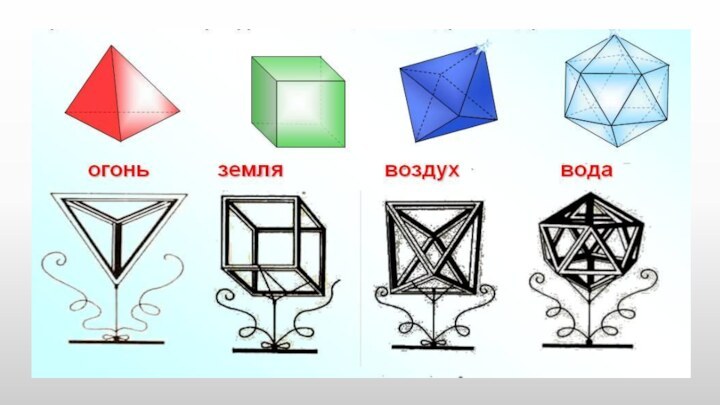
всех сторон плоскими многоугольниками, называемыми гранями. Стороны граней называются

ребрами многогранника, а концы ребер — вершинами многогранника. Многогранник называется выпуклым, если он весь расположен по одну сторону от плоскости каждой из его граней. Многогранник называется правильным, если:
1. он выпуклый
2. все его грани являются равными правильными многоугольниками
3. в каждой его вершине сходится одинаковое число граней
4. все его двугранные углы равны

от греческого наименования количества его граней и слова грань

- эдра:
тетра – 4,
гекса – 6
окто – 8
додек – 12
икоси - 20

Они имеют одинаковые свойства:
• Все грани имеют один и тот же размер
• Все ребра имеют одинаковую длину
• Все углы тела равны
• Все тела можно вписать в сферу

грани – равносторонние треугольники. Каждая его вершина является вершиной

трех треугольников. Все многогранные углы тетраэдра равны между собой. Сумма плоских углов при каждой вершине равна 180°. Таким образом, тетраэдр имеет 4 грани, 4 вершины и 6 ребер.

Гексаэдр
Гексаэдр или куб составлен из шести квадратов. Каждая его вершина является вершиной трех квадратов. Сумма плоских углов при каждой вершине равна 270°. Таким образом, куб имеет 6 граней, 8 вершин и 12 ребер

вершина является вершиной четырех треугольников. Противоположные грани лежат в

параллельных плоскостях. Сумма плоских углов при каждой вершине равна 240°. Таким образом, октаэдр имеет 8 граней, 6 вершин и 12 ребер.

Икосаэдр
Икосаэдр – одно из пяти платоновых тел, по простоте следующее за тетраэдром и октаэдром. Икосаэдр составлен из двадцати равносторонних треугольников. Каждая его вершина является вершиной пяти треугольников. Сумма плоских углов при каждой вершине равна 300°. Таким образом, икосаэдр имеет 20 граней, 12 вершин и 30 ребер.

вершина является вершиной трех пятиугольников. Сумма плоских углов при

каждой вершине равна 324°. Таким образом, додекаэдр имеет 12 граней, 20 вершин и 30 ребер.

так называемым свойством взаимности:
центры граней куба являются вершинами

правильного октаэдра, а центры граней правильного октаэдра являются вершинами куба.
Если соединять отрезками центры соседних граней куба, то эти отрезки станут ребрами октаэдра;
если проделать ту же операцию с октаэдром, получится куб. Число вершин октаэдра равно числу граней куба, и наоборот; более того, количества ребер у них совпадают.

граней додекаэдра являются вершинами икосаэдра,
а центры граней икосаэдра –

вершинами додекаэдра.

Куб и октаэдр, додекаэдр и икосаэдр – это две пары двойственных многогранников. У них одинаковое число рёбер (12 – у куба и октаэдра; 30 – у додекаэдра и икосаэдра), а числа вершин и граней переставлены.

Тетраэдр двойствен сам себе.

Особняком стоит тетраэдр: если соединить отрезками центры его граней, то вновь получится тетраэдр.

уже были известны людям неолита, по крайней мере, за

1000 лет до Платона. Найдены древние сферические камни, которые покрыты геометрически точными фигурами куба, тетраэдра, октаэдра, икосаэдра и додекаэдра.
Но почему они называются Платоновыми телами?
Эти правильные многогранники получили такое название по имени древнегреческого философа Платона (428-348 до н э.), который придавал им мистический смысл.
Он считал, что вся Вселенная имеет форму додекаэдра, а материя состоит из атомов, которые имеют форму тетраэдров, кубов, октаэдров и икосаэдров.

Для возникновения данных ассоциаций были следующие причины:

вверх, как у разгоревшегося пламени, жар огня ощущается чётко

и остро (как маленькие тетраэдры).
Икосаэдр - как самый обтекаемый – воду, вода выливается, если её взять в руку, как будто она сделана из множества маленьких шариков (к которым ближе всего икосаэдры).
Гексаэдр - самая устойчивая из фигур - землю.
Октаэдр – воздух, его мельчайшие компоненты настолько гладкие, что их с трудом можно почувствовать; .
Додекаэдр отождествлялся со всей Вселенной и почитался главнейшим.

Примечательно, что все пять Платоновых тел в разные времена использовались в качестве игральных костей.

сделан в XVIII веке Леонардом Эйлером, который «проверил алгеброй

гармонию».
Теорема Эйлера о соотношении между числом вершин, ребер и граней выпуклого многогранника, навела математический порядок в мире многогранников.
Вершины + Грани - Рёбра = 2.
Эта формула верна для любого многогранника.

Правильные многогранники встречаются в живой природе. Например, скелет одноклеточного организма феодарии  по форме напоминает икосаэдр.
Кристалл пирита (сернистого колчедана,) имеет форму додекаэдра.

для которого правильные многогранники были любимым предметом изучения, развил

учение о двух видах выпуклых звездчатых многогранников.

В 1619 году им были открыты малый звёздчатый додекаэдр

и большой звёздчатый додекаэдр

И только почти 200 лет спустя другой ученый Луи Пуансо открыл
большой додекаэдр

и большой икосаэдр.