- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Различные подходы к доказательству теоремы Пифагора
Содержание
- 2. На протяжении веков были даны многочисленные разные
- 3. Теорема Пифагора в древнейшем китайском трактате «Чжоу-би»Теорема
- 4. Если на гипотенузе и катетах прямоугольного треугольника
- 5. Доказательство:DBC = FBA = 900DBC +ABC =FBA
- 6. В треугольнике ABD высота, проведенная из вершины
- 7. В треугольнике FBC высота, проведенная из вершины
- 8. BCE = ACK = 900BCE
- 9. В треугольнике ACE высота, проведенная из вершины
- 10. В треугольнике BKC высота, проведенная из вершины
- 11. Но SBJLD + SJCEL = SBCED, Тогда
- 12. Доказательство Анариция, основанное на том, что
- 13. Доказательство, основанное на теории подобияЛеонардо Фибоначчи и
- 14. Из подобия треугольников ACD и CAB следует:Из
- 15. Алгебраический метод БхаскарыБхаскара(1114 -1185) индийский
- 16. Скачать презентацию
- 17. Похожие презентации






Слайд 2 На протяжении веков были даны многочисленные разные доказательства
теоремы Пифагора...
рукописи
Слайд 3
Теорема Пифагора в древнейшем китайском трактате «Чжоу-би»
Теорема Пифагора
упоминается в первой части самого древнего дошедшего до нас
китайского математико-астрономического сочинения «Чжоу-би», написанного около 1100 лет до н.э.Прокл в своем комментарии к «Началам» Евклида пишет относительно предложения о том, что квадрат гипотенузы равен сумме квадратов катетов, следующее: «Если слушать тех, кто любит повторять древние легенды, то придется сказать, что эта теорема восходит к Пифагору. Рассказывают, что в честь этого открытия он принес в жертву быка». О том же рассказывает и другой греческий историк древности – Плутарх (I в.). На основе этих и других преданий долгое время считали, что до Пифагора эта теорема не была известна и назвали ее поэтому «теоремой Пифагора»…
Однако теперь известно, что эта важнейшая теорема встречается в вавилонских текстах, написанных за 1200 лет до Пифагора.
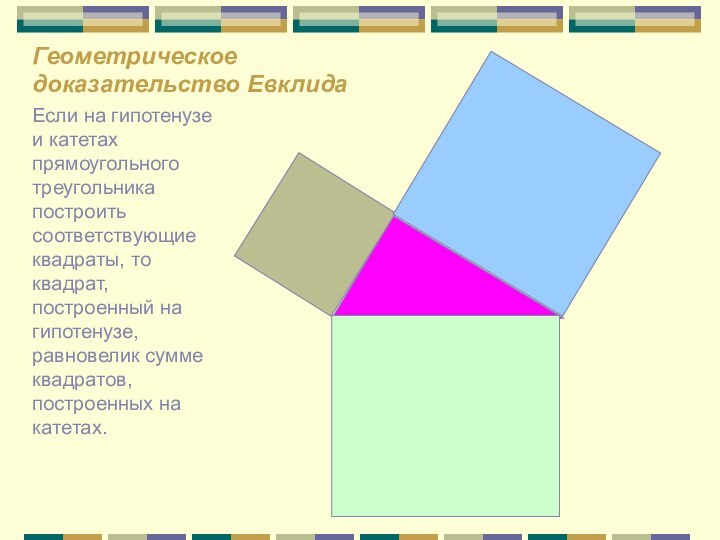
Слайд 4 Если на гипотенузе и катетах прямоугольного треугольника построить
соответствующие квадраты, то квадрат, построенный на гипотенузе, равновелик сумме
квадратов, построенных на катетах.Геометрическое доказательство Евклида
Слайд 5
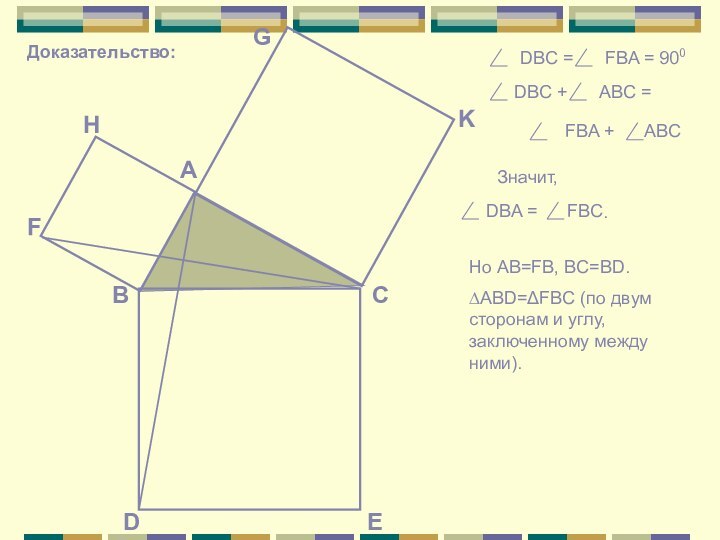
Доказательство:
DBC =
FBA = 900
DBC +
ABC =
FBA +
ABC
Значит,
DBA = FBC
.
Но AB=FB, BC=BD.
∆ABD=ΔFBC
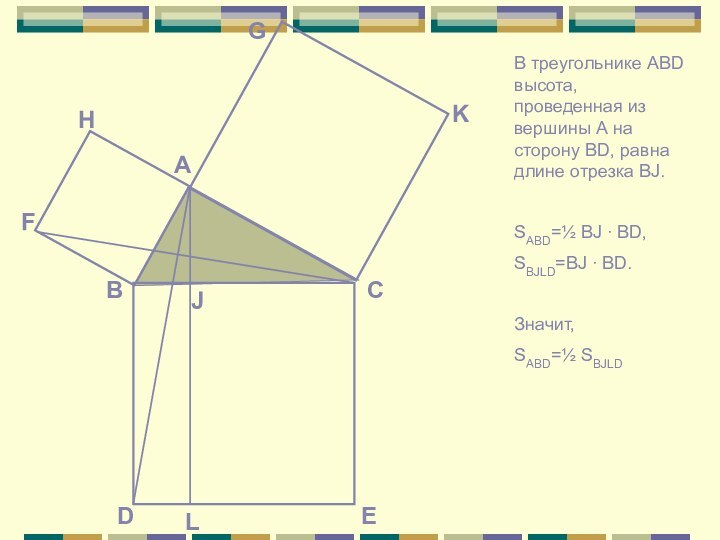
(по двум сторонам и углу, заключенному между ними).Слайд 6 В треугольнике ABD высота, проведенная из вершины А
на сторону BD, равна длине отрезка BJ.
SABD=½ BJ ∙
BD,SBJLD=BJ ∙ BD.
Значит,
SABD=½ SBJLD
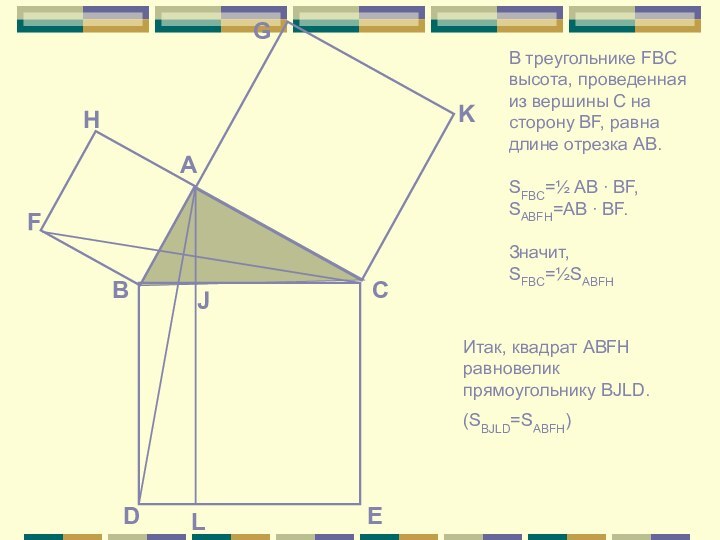
Слайд 7 В треугольнике FBC высота, проведенная из вершины C
на сторону BF, равна длине отрезка AB.
SFBC=½ AB ∙
BF,SABFH=AB ∙ BF.
Значит,
SFBC=½SABFH
Итак, квадрат ABFH равновелик прямоугольнику BJLD.
(SBJLD=SABFH)
Слайд 8
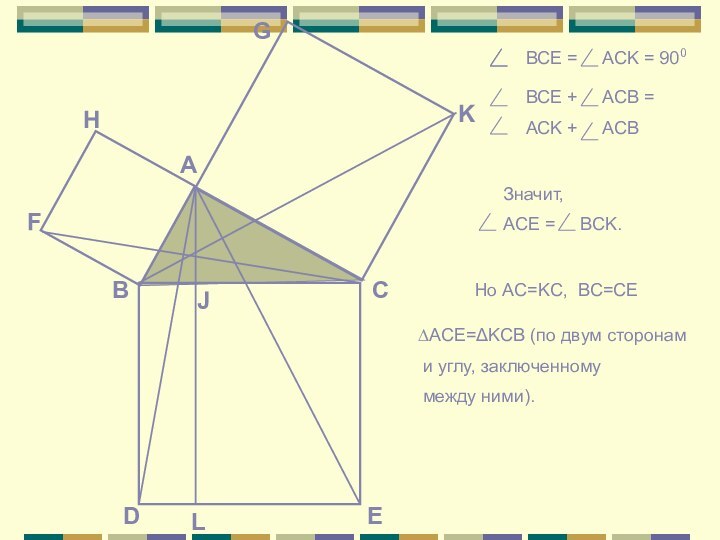
BCE = ACK = 900
BCE +
ACB =
ACK + ACB
Значит,
ACE =
BCK.Но AC=KC, BC=CE
∆ACE=ΔKCB (по двум сторонам
и углу, заключенному
между ними).
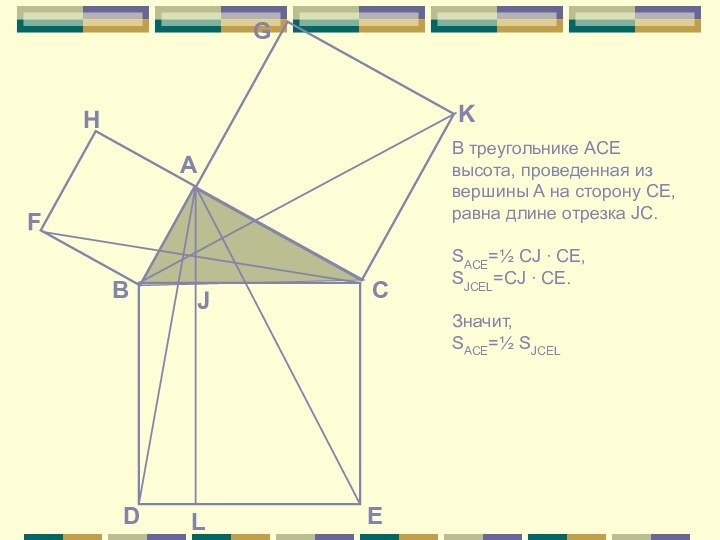
Слайд 9 В треугольнике ACE высота, проведенная из вершины А
на сторону CE, равна длине отрезка JC.
SACE=½ CJ ∙
CE,SJCEL=CJ ∙ CE.
Значит,
SACE=½ SJCEL
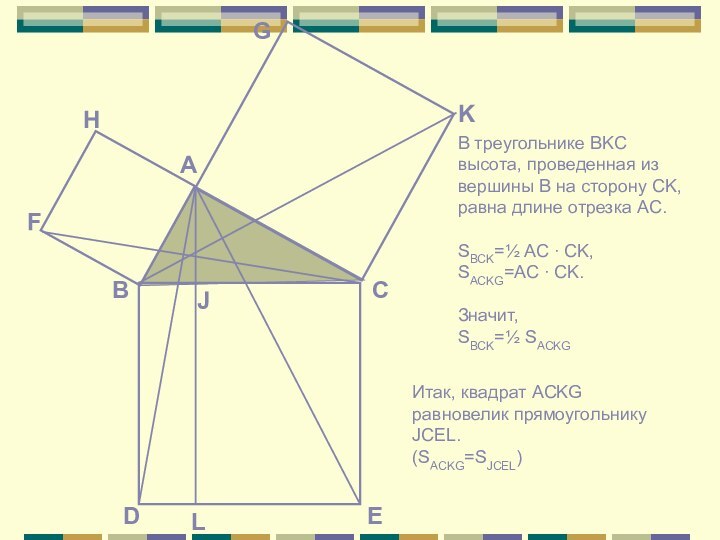
Слайд 10 В треугольнике BKC высота, проведенная из вершины B
на сторону CK, равна длине отрезка AC.
SBCK=½ AC ∙
CK,SACKG=AC ∙ CK.
Значит,
SBCK=½ SACKG
Итак, квадрат ACKG равновелик прямоугольнику JCEL.
(SACKG=SJCEL)
Слайд 11
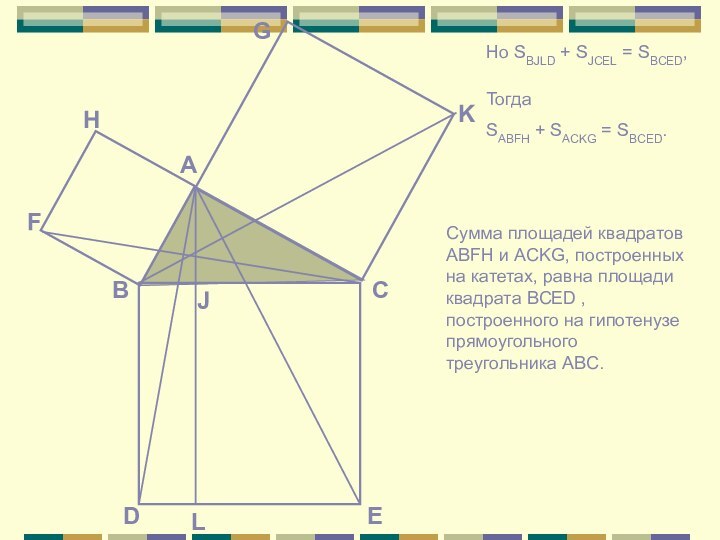
Но SBJLD + SJCEL = SBCED,
Тогда
SABFH +
SACKG = SBCED.
Сумма площадей квадратов ABFH и ACKG, построенных
на катетах, равна площади квадрата BCED , построенного на гипотенузе прямоугольного треугольника ABC.
Слайд 12
Доказательство Анариция,
основанное на том, что
равносоставленные фигуры равновелики
Чертеж
к доказательству Анариция
Если на гипотенузе и катетах прямоугольного треугольника
построить соответствующие квадраты, то квадрат, построенный на гипотенузе, равновелик сумме квадратов, построенных на катетах.Доказательство основывается на том, что равносоставленные фигуры равновелики: квадраты, построенные на катетах и гипотенузе, разбиваются на многоугольники так, что каждому многоугольнику из состава квадрата на гипотенузе соответствует равный многоугольник одного из квадратов на катетах.
Достаточно посмотреть на чертеж, чтобы понять все доказательство (см. рис.).
Это доказательство дал багдадский математик и астроном X в. ан-Найризий (латинизированное имя – Анариций).
Слайд 13
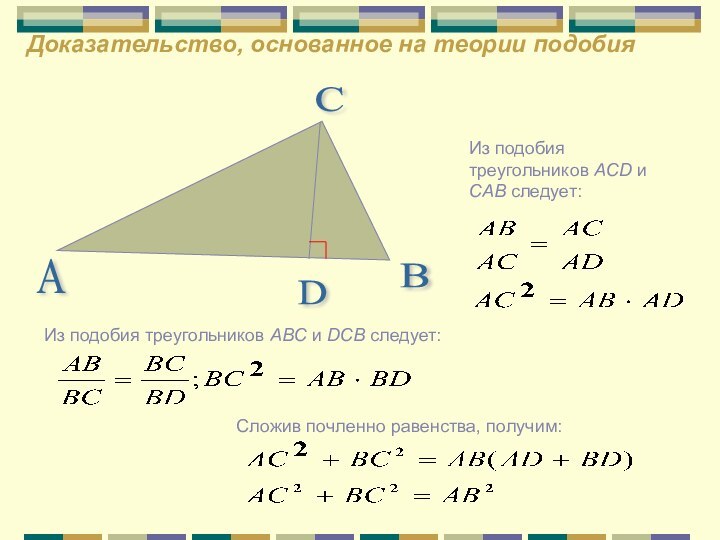
Доказательство, основанное на теории подобия
Леонардо Фибоначчи и Валлис
(XVII в.) "Практическая геометрия"
Лежандр (VIII в.)
А.Ю. Давидов "Элементарная геометрия"
Слайд 14
Из подобия треугольников ACD и CAB следует:
Из подобия
треугольников ABC и DCB следует:
Сложив почленно равенства, получим:
Доказательство, основанное
на теории подобия
Слайд 15
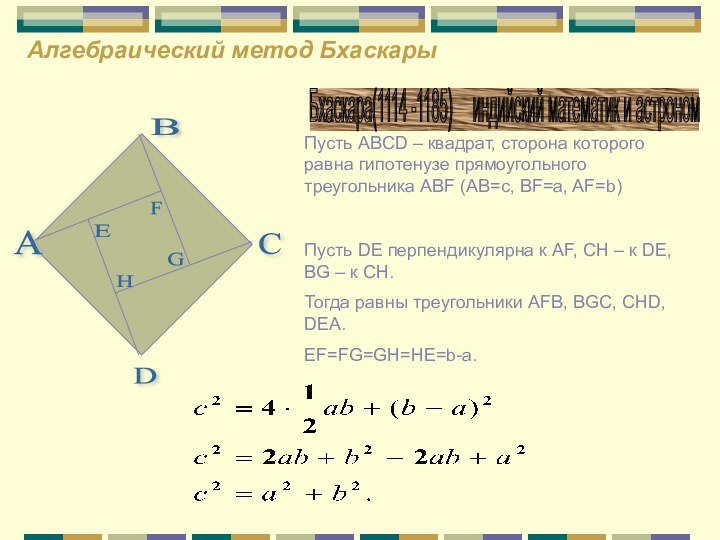
Алгебраический метод Бхаскары
Бхаскара(1114 -1185) индийский математик
и астроном
А
С
D
H
В
G
F
E
Пусть ABCD – квадрат, сторона которого равна гипотенузе прямоугольного треугольника ABF (AB=c, BF=a, AF=b)
Пусть DE перпендикулярна к AF, CH – к DE, BG – к CH.
Тогда равны треугольники AFB, BGC, CHD, DEA.
EF=FG=GH=HE=b-a.





























