Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Симметрия и симметричные фигуры

Содержание

2. “Симметрия является той идеей, посредством которой человек
3. Определение симметрииСимметрия (от греческого symmetria - "соразмерность") -
4. Симметрия в математике Простейшими видами пространственной симметрии являются центральная, осевая, зеркально- поворотная и симметрия переноса.
5. Геометрическая фигура называется симметричной относительно центра C
6. Примеры центральной симметрии
7. Фигура называется симметричной, если для каждой точки
8. У неразвёрнутого угла одна ось симметрии -
9. Прямоугольник и ромб, не являющиеся квадратами имеют
11. Поворотом фигуры F вокруг центра O на данный угол φ в данном направлении называется
12. Примеры зеркально-поворотной симметрии
13. Имеют вертикальную ось симметрии буквы:Имеют Горизонтальную ось
14. палиндромыКАЗАК ШАЛАШИСКАТЬ ТАКСИАРГЕНТИНА МАНИТ НЕГРАЛЕША НА ПАЛКЕ КЛАПАНА НАШЕЛ
15. Скачать презентацию
16. Похожие презентации

“Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство”.Г. Вейль

Главная
Математика
Симметрия и симметричные фигуры

Подготовила: Еремеева Мария 11«Г»Симметрия

“Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь

Определение симметрииСимметрия (от греческого symmetria -

Симметрия в математике Простейшими видами пространственной симметрии являются центральная, осевая, зеркально- поворотная и симметрия переноса.

Геометрическая фигура называется симметричной относительно центра C , если для каждой точки

Фигура называется симметричной, если для каждой точки E этой фигуры может быть

У неразвёрнутого угла одна ось симметрии - прямая, на которой расположена биссектриса

Прямоугольник и ромб, не являющиеся квадратами имеют по две оси симметрии, а

Поворотом фигуры F вокруг центра O на данный угол φ в данном направлении называется такое ее преобразование, при котором

Имеют вертикальную ось симметрии буквы:Имеют Горизонтальную ось симметрии буквы:Имеют по две оси

палиндромыКАЗАК ШАЛАШИСКАТЬ ТАКСИАРГЕНТИНА МАНИТ НЕГРАЛЕША НА ПАЛКЕ КЛАПАНА НАШЕЛ

Слайды презентации

Слайд 2 “Симметрия является той идеей, посредством которой человек на

“Симметрия является той идеей, посредством которой человек на протяжении веков пытался

протяжении веков пытался постичь и создать порядок, красоту и совершенство”.
Г.

Вейль

Слайд 3 Определение симметрии
Симметрия (от греческого symmetria - "соразмерность") - понятие,

означающее сохраняемость, повторяемость, "инвариантность" каких-либо особенностей структуры изучаемого объекта

при проведении с ним определенных преобразований.

Слайд 4 Симметрия в математике
Простейшими видами пространственной симметрии являются центральная,

осевая, зеркально- поворотная и симметрия переноса.

Слайд 5 Геометрическая фигура называется симметричной относительно центра C ,

Геометрическая фигура называется симметричной относительно центра C , если для каждой

если для каждой точки A этой фигуры может быть

найдена точка E этой же фигуры, так что отрезок AE проходит через центр C и делится в этой точке. Точка C называется центром симметрии.

Центральную симметрию имеют многие геометрические тела. К ним следует отнести все правильные многогранники (за исключением тетраэдра), все правильные призмы и некоторые тела вращения (цилиндр, шар). Простейшими фигурами, обладающими центральной симметрией, является окружность.

1.Центральная симметрия

Слайд 6 Примеры центральной симметрии

Слайд 7 Фигура называется симметричной, если для каждой точки E

Фигура называется симметричной, если для каждой точки E этой фигуры может

этой фигуры может быть найдена точка E’ этой же

фигуры, так что отрезок EE’ перпендикулярен плоскости S и делится этой плоскостью пополам. Симметричные фигуры, предметы и тела не равны друг другу. Они называются зеркально равными.

Две точки называются симметричными относительно прямой, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему.

2. Осевая симметрия

Слайд 8 У неразвёрнутого угла одна ось симметрии - прямая,

У неразвёрнутого угла одна ось симметрии - прямая, на которой расположена

на которой расположена биссектриса угла.
Равнобедренный (но не равносторонний) треугольник

имеет также одну ось симметрии. А равносторонний треугольник - три основные симметрии.

Примеры осевой симметрии

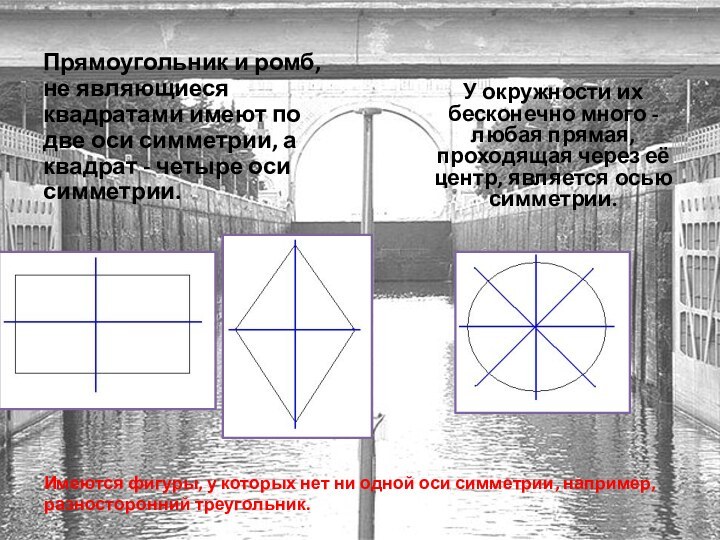
Слайд 9 Прямоугольник и ромб, не являющиеся квадратами имеют по

Прямоугольник и ромб, не являющиеся квадратами имеют по две оси симметрии,

две оси симметрии, а квадрат - четыре оси симметрии.
У

окружности их бесконечно много - любая прямая, проходящая через её центр, является осью симметрии.

Имеются фигуры, у которых нет ни одной оси симметрии, например, разносторонний треугольник.

Слайд 10

Слайд 11 Поворотом фигуры F вокруг центра O на данный угол φ в данном направлении называется такое

Поворотом фигуры F вокруг центра O на данный угол φ в данном направлении называется такое ее преобразование, при

ее преобразование, при котором каждой точке X F сопоставляется точка так, что и луч откладывается

от луча OX в заданном направлении. Точка O называется центром поворота, а угол φ – углом поворота ). Множеством неподвижных точек преобразования поворота является центр поворота.

3. Зеркально-поворотная симметрия