- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Тригонометрические выражения и их преобразования
Содержание
- 2. Определение синуса, косинуса, тангенса и котангенса.
- 3. Проведём два диаметра: горизонтальный AA’ и вертикальный BB’. Будем
- 4. Знаки синуса и косинуса в различных четвертях единичного круга.
- 5. Линия синуса угла ( рис.4 ) - это вертикальный диаметр единичного круга, линия косинуса угла - горизонтальный диаметр единичного круга. Синус угла ( рис.4 )
- 6. Линия тангенса ( рис.7 ) – это касательная
- 7. Знаки тангенса и котангенса в различных четвертях единичного круга показаны на рис.9.
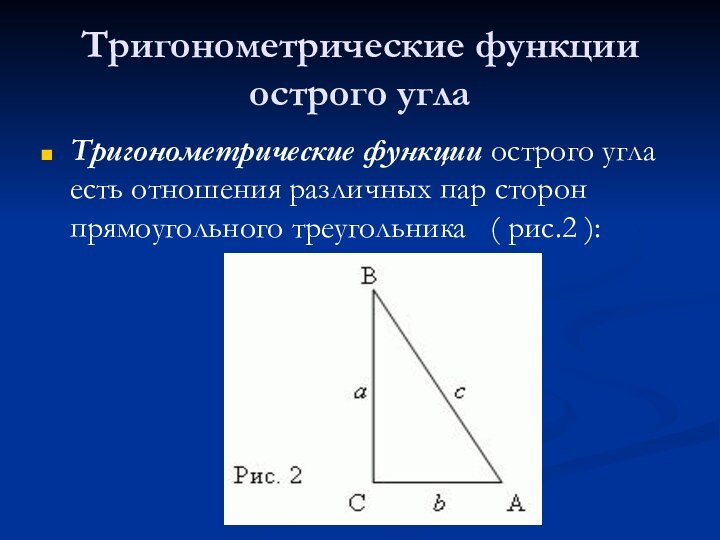
- 8. Тригонометрические функции острого углаТригонометрические функции острого угла есть отношения различных пар сторон прямоугольного треугольника ( рис.2 ):
- 9. Тригонометрические функции острого угла: синус, косинус, тангенс,
- 10. Прямоугольный треугольник ABC ( рис.2 )
- 11. Для некоторых углов можно записать точные значения их тригонометрических функций. Наиболее важные случаи приведены в таблице:
- 12. Углы 0° и 90°, строго говоря,не являются острыми
- 13. Решение прямоугольных треугольников По двум сторонам. По
- 14. П р и м е р 1.Катет a =
- 15. П р и м е р 2.
- 16. По стороне и острому углу.. Если задан один острый угол A, то другой острый угол B находится из
- 17. П р и м е р .
- 18. Радианное и градусное измерение углов Градусная мера. Здесь единицей измерения является градус ( обозначение ° ) – это поворот луча
- 19. Радианная мера . Как мы
- 20. Следуя этой формуле, длину окружности C и её радиус r можно
- 21. Полезно помнить следующую сравнительную таблицу значений наиболее часто встречающихся углов в градусах и радианах:
- 22. Соотношения между тригонометрическими функциями одного и того
- 23. п-33. Формулы приведения
- 24. п-33. Формулы приведения
- 25. п-33. Формулы приведенияЭти формулы позволяют: 1) найти численные
- 27. п 34. Формулы сложения и вычитания
- 28. п 34. Формулы сложения и вычитания
- 29. Основные соотношения между элементами треугольника.Теорема косинусов. Теорема
- 30. Теорема косинусов:
- 31. Теорема синусов:
- 32. Теорема тангенсов:
- 33. Формулы площади, формула Герона:
- 34. Радиусы описанного и вписанного кругов:
- 35. Решение косоугольных треугольников. Заданы три стороны a, b, c . Найти углы A, B, C. По теореме косинусов находим один из углов:
- 36. второй угол находим по теореме синусов: третий
- 37. П р и м е р . Заданы три стороны треугольника: a = 2, b = 3, c = 4. Найти его углы.
- 38. Дано: две стороны a и b и угол C между ними. Найти сторону c и
- 39. Даны две стороны a и b и угол B, противоположный одной из
- 40. Здесь возможны следующие случаи: 1) a > b ; a · sin B > b – здесь
- 41. После нахождения угла A, найдём третий угол: C =
- 42. Если угол C имеет два значения, то и сторона c имеет
- 43. Р е ш е н и е Здесь: a > b и a sin B
- 44. Скачать презентацию
- 45. Похожие презентации
Определение синуса, косинуса, тангенса и котангенса. Чтобы построить всю тригонометрию, законы которой были бы справедливы для любых углов (не только для острых, но и для тупых, положительных и отрицательных углов ), необходимо рассмотреть так называемый единичный круг, то есть круг,











































Слайд 2
Определение синуса, косинуса, тангенса и котангенса.
Чтобы построить всю тригонометрию, законы которой
(не только для острых, но и для тупых, положительных и отрицательных углов ), необходимо рассмотреть так называемый единичный круг, то есть круг, радиус которого равен 1 ( рис.3 ).Слайд 3 Проведём два диаметра: горизонтальный AA’ и вертикальный BB’. Будем отсчитывать углы от точки A ( начальная точка ). Отрицательные углы отсчитываются по часовой стрелке,
положительные – против. Подвижный радиус OC образует угол с неподвижным радиусом OA.Он может быть расположен в 1-ой четверти ( COA ), во 2-ой четверти ( DOA ), в
3-ей четверти (EOA ) или в 4-ой четверти ( FOA ). Считая OA и OB положительными направлениями, а OA’ и OB’ – отрицательными, мы определим тригонометрические функции следующим образом.
Слайд 5 Линия синуса угла ( рис.4 ) - это вертикальный диаметр единичного круга, линия косинуса угла - горизонтальный диаметр единичного круга. Синус угла ( рис.4 ) –
это отрезок OB на линиисинуса, то есть проекция подвижного радиуса OK на линию синуса; косинус угла - отрезок OAлинии косинуса, то есть проекция подвижного радиуса OK на линию косинуса. Знаки синуса
и косинуса в различных четвертях единичного круга показаны на рис.5 и рис.6.Слайд 6 Линия тангенса ( рис.7 ) – это касательная к
единичному кругу, проведенная через точку A горизонтального диаметра. Линия котангенса ( рис.8 ) –
это касательная к единичному кругу, проведенная через точку В вертикального диаметра. Тангенс – это отрезок линии тангенса между точкой касания A и точкой пересечения ( D, E, и т.д., рис.7 ) линии тангенса и линии радиуса. Котангенс – это отрезок линии котангенса между точкой касания В и точкой пересечения ( Р, Q, и т.д., рис.8 ) линии котангенса и линии радиуса.Знаки синуса и косинуса в различных четвертях единичного круга
Слайд 8
Тригонометрические функции острого угла
Тригонометрические функции острого угла есть отношения
различных пар сторон прямоугольного треугольника ( рис.2 ):
Слайд 9 Тригонометрические функции острого угла: синус, косинус, тангенс, котангенс, секанс,
косеканс.
1) Синус - отношение противолежащего катета к гипотенузе: sin A = a / c .
2) Косинус
- отношение прилежащего катета к гипотенузе: cos A = b / c .3) Тангенс - отношение противолежащего катета к прилежащему: tan A = a / b .
4) Котангенс - отношение прилежащего катета к противолежащему: cot A = b / a .
5) Секанс - отношение гипотенузы к прилежащему катету: sec A = c / b .
6) Косеканс - отношение гипотенузы к противолежащему катету: cosec A = c / a .
Слайд 10 Прямоугольный треугольник ABC ( рис.2 ) имеет катеты: a =
4, b = 3. Найти синус, косинус и тангенс угла A.
Р е
ш е н и е . Во-первых, найдём гипотенузу, используя теорему Пифагора:c 2 = a 2 + b 2 ,
Согласно вышеприведенным формулам имеем:
sin A = a / c = 4 / 5; cos A = b / c = 3 / 5; tan A = a / b = 4 / 3.
Слайд 11 Для некоторых углов можно записать точные значения их
тригонометрических функций.
Наиболее важные случаи приведены в таблице:
Слайд 12
Углы 0° и 90°, строго говоря,
не являются острыми в
прямоугольном треугольнике, однако при расширении понятия тригонометрических функций эти
углы также рассматриваются.Символ в таблице означает, что абсолютное значение функции неограниченно возрастает, если угол приближается к указанному значению.
Слайд 13 Решение прямоугольных треугольников По двум сторонам. По стороне и
острому углу.
По двум сторонам. Если заданы две стороны прямоугольного треугольника, то третья
сторона вычисляется по теореме Пифагора.Острые углы могут быть определены по одной из трёх первых формул для тригонометрических функций в зависимости от того, какие стороны известны. Например, если заданы катеты a и b , то угол A определяется по формуле:
tan A = a / b .
Слайд 14 П р и м е р 1.Катет a = 0.324,
гипотенуза
c = 0.544. Найти второй катет b и углы A и B.
Р е ш е
н и е .Катет b равен:Слайд 15 П р и м е р 2. Даны
два катета: a = 7.2 см,
b = 6.4 см. Найти гипотенузу и углы A и B.
Р
е ш е н и е .Гипотенуза c равна:
Слайд 16
По стороне и острому углу.
. Если задан один острый угол A, то другой острый угол B находится из равенства:
B =
90° - A. Стороны находятся по формулам тригонометрических функций, переписанных в виде:
a
= c sin A , b = c cos A , a = b tan A ,b = c sin B , a = c cos B , b = a tan B .
Остаётся выбрать те формулы, которые содержат заданную или уже найденную сторону.
Слайд 17 П р и м е р . Дано:
гипотенуза c = 13.65 м и острый угол A = 54°17’. Найти другой острый
угол B и катеты a и b .
Слайд 18
Радианное и градусное измерение углов
Градусная мера.
Здесь единицей измерения является градус
( обозначение ° ) – это поворот луча на 1 / 360 часть
одного полного оборота. Таким образом, полный оборот луча равен 360°. Один
градус состоит из 60 минут ( их обозначение ‘ ); одна минута – соответственно из 60 секунд (обозначаются “ ).
Слайд 19
Радианная мера .
Как мы знаем
из планиметрии длина дуги l , радиус r и соответствующий центральный угол а связаны соотношением:
а = l /
r .Эта формула лежит в основе определения радианной меры измерения углов. Так, если l = r , то а = 1, и мы говорим, что угол равен 1 радиану, что обозначается: а = 1 рад. Таким образом, мы имеем следующее определение радианной меры измерения:
Слайд 20 Следуя этой формуле, длину окружности C и её радиус r можно выразить
следующим образом:
2 = C / r .
Так, полный оборот, равный 360° в
градусном измерении, соответствует 2 в радианном измерении. Откуда мы получаем значение одного радиана, и обратно:Слайд 21 Полезно помнить следующую сравнительную таблицу значений наиболее часто
встречающихся углов в градусах и радианах:
Слайд 22 Соотношения между тригонометрическими функциями одного и того же угла.
Эти формулы являются основными тригонометрическими тождествами.
Слайд 25
п-33. Формулы приведения
Эти формулы позволяют:
1) найти численные значения
тригонометрических функций углов, бо’льших 90°;
2) выполнить преобразования, приводящие к
более простым выражениям;3) избавиться от отрицательных углов и углов, бо’льших 360°.
Слайд 29
Основные соотношения между элементами треугольника.
Теорема косинусов. Теорема синусов.
Теорема тангенсов.
Формулы площади, формула Герона.
Радиусы описанного и вписанного кругов
Обозначения: a, b, c – стороны;
A, B, C – углы; p = ( a + b + c ) / 2 - полупериметр; h –высота;
S – площадь; R – радиус описанного круга;
r – радиус вписанного круга.
Слайд 35
Решение косоугольных треугольников.
Заданы три стороны a, b, c . Найти углы A, B, C.
По теореме
косинусов находим один из углов:
Слайд 36
второй угол находим по теореме синусов:
третий угол
находится по формуле:
C = 180° – ( A + B ).
Слайд 38 Дано: две стороны a и b и угол C между ними. Найти сторону c и углы A и B. По
теореме косинусов находим сторону c :
c 2 = a 2 + b 2 - 2 ab · cos C ;
а затем
по теореме синусов – угол A : здесь необходимо подчеркнуть, что A – острый угол, если b / a > cos C, и тупой угол, если b / a < cos C. Третий угол B = 180° - ( A + C ).
Слайд 39 Даны две стороны a и b и угол B, противоположный одной из них. Найти
сторону c и углы A и C.
Сначала по теореме синусов найдём угол A:
Заданы любые два
угла и сторона.
Найти третий угол и две другие стороны.
Очевидно, что третий угол вычисляется по формуле:
A+ B+ C = 180°,
и тогда используя теорему синусов, мы найдём две другие стороны.
Слайд 40
Здесь возможны следующие случаи:
1) a > b ; a · sin B > b – здесь решения
нет;
2) a > b ; a · sin B = b – здесь одно решение, A – прямой угол;
3) a > b ; a · sin B
– здесь два решения: A может быть либо острым, либо тупым углом;4) a b – здесь одно решение, A – острый угол.
Слайд 41
После нахождения угла A, найдём третий угол:
C = 180°
- ( A+ B ). Если A может иметь два значения, то и C может иметь два значения.
Теперь по теореме синусов можно найти третью сторону:
Слайд 42
Если угол C имеет два значения,
то и сторона c имеет два
значения, следовательно, заданным условиям удовлетворяют два различных треугольника.
Дано: a = 5, b = 3, B =
30°.Найти сторону c и углы A и C.