- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Векторы. Модуль вектора. Равенство векторов. Сложение векторов
Содержание
- 2. Направления отрезка
- 3. ВекторОпределение. Отрезок, для которого указано, какой
- 4. Вектор Векторы обозначают: или
- 5. Нулевой векторОпределение. Нулевой вектор – это вектор,начало
- 6. Длина вектораОпределение. Длиной ненулевого вектора называется длина
- 7. Коллинеарные векторыОпределение. Два ненулевых вектора называются коллинеарными,
- 8. Сонаправленные векторыОпределение. Два ненулевых вектора называютсясонаправленными, если
- 9. Противоположные векторы Определение. Два ненулевых вектора
- 10. Равные векторыОпределение. Векторы называются равными, если они
- 11. Правило треугольникаОпределение. Суммой двух векторов
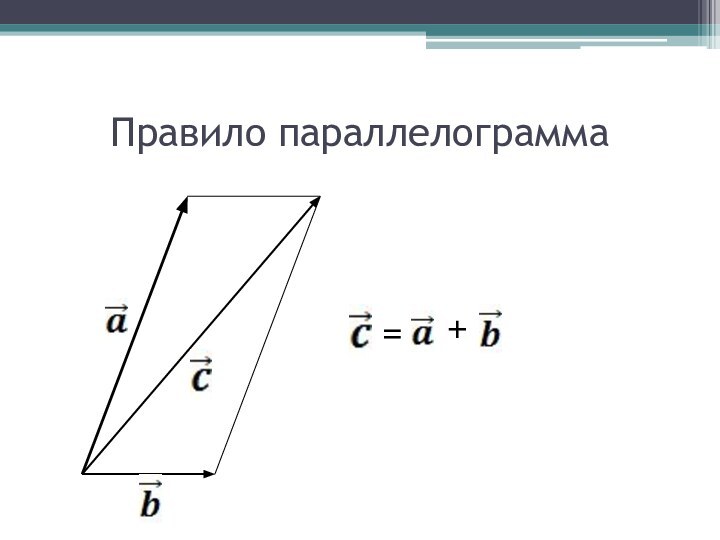
- 12. Правило параллелограмма = +
- 13. Определение. Суммой нескольких векторов ,
- 14. Задание № 11 подгруппа – сонаправленных векторов,2
- 15. Задание № 21 подгруппа –
- 16. Вопросы:Что такое вектор?Что понимают под длинной или
- 17. Домашнее заданиеСборник задач по математике А.А. Дадаян:№ 3.2.№ 3.3.№ 3.5.
- 18. Скачать презентацию
- 19. Похожие презентации
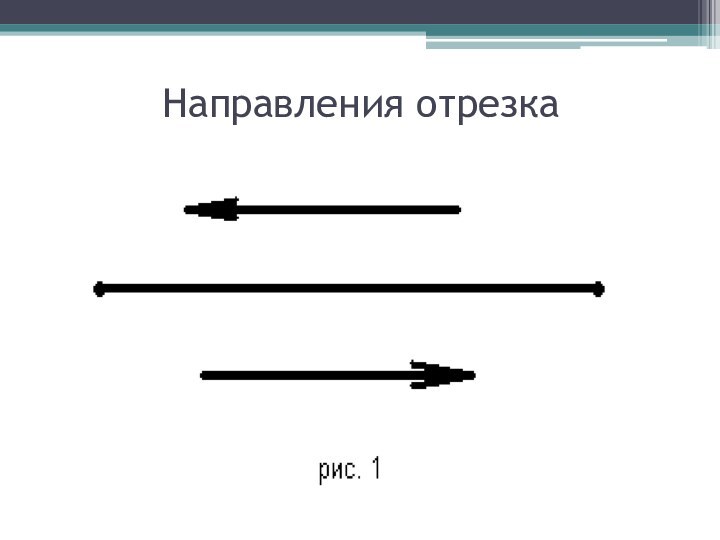
Направления отрезка











Слайд 3
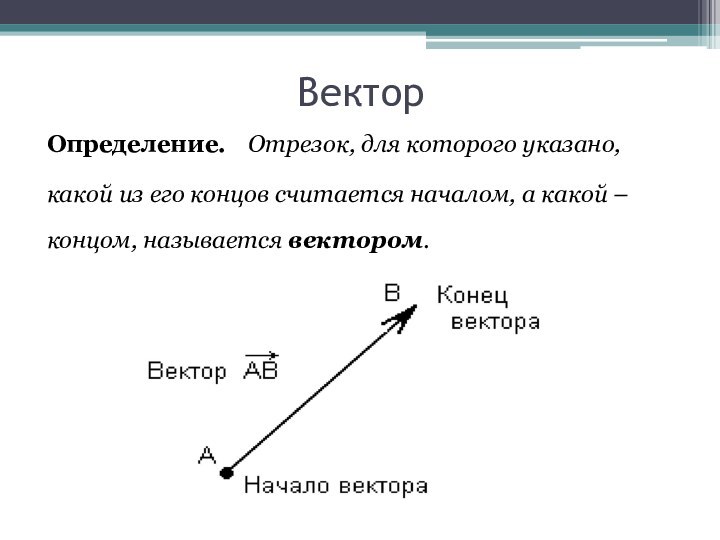
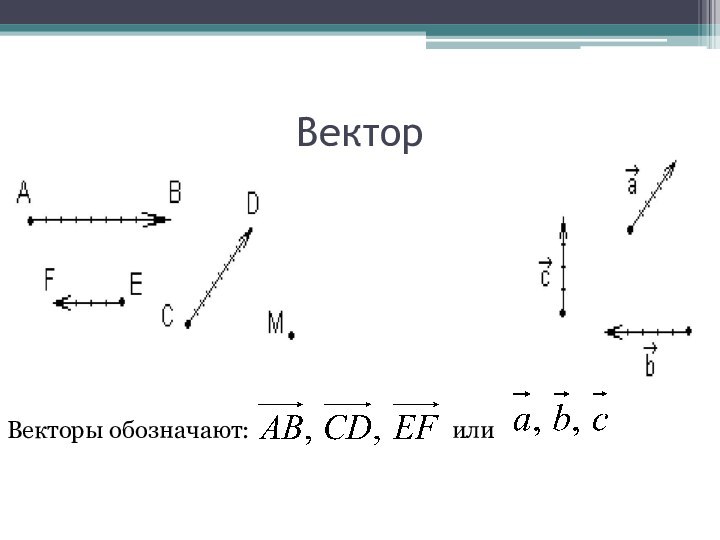
Вектор
Определение. Отрезок, для которого указано,
какой из
его концов считается началом, а какой –
вектором.
Слайд 5
Нулевой вектор
Определение. Нулевой вектор – это вектор,
начало и
конец которого совпадают. Направление
нулевого вектора считается неопределенным.
М
- нулевой
вектор
Слайд 6
Длина вектора
Определение. Длиной ненулевого вектора называется длина отрезка
АВ.
Длина вектора (вектора
) обозначается так: ( ).
Длина нулевого вектора: = 0.
Слайд 7
Коллинеарные векторы
Определение. Два ненулевых вектора называются
коллинеарными, если
они лежат на одной прямой
или на параллельных прямых.
–
коллинеарны– коллинеарны
– коллинеарны
Слайд 8
Сонаправленные векторы
Определение. Два ненулевых вектора называются
сонаправленными, если они
коллинеарны и
направлены в одну сторону.
⇈
– сонаправленные векторы
⇅
– противоположно направленные
векторы
Слайд 9
Противоположные векторы
Определение. Два ненулевых вектора называются
противоположными друг другу, если они имеют одинаковые модули, коллинеарны
и противоположнонаправленные.
⇅
и
противоположно направленные
противоположные векторы
Слайд 10
Равные векторы
Определение. Векторы называются равными, если
они сонаправленны
и их длины равны.
Теорема. От любой точки можно отложить
вектор, равный данному, и притом только один., так как
⇈
и
=
а
≠
, так как
⇅
Слайд 11
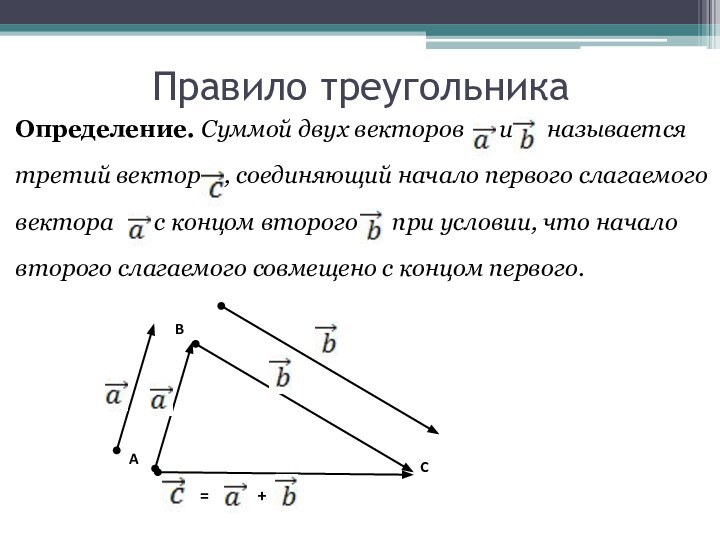
Правило треугольника
Определение. Суммой двух векторов и
называется
третий вектор , соединяющий начало первого
слагаемоговектора с концом второго при условии, что начало
второго слагаемого совмещено с концом первого.
Слайд 13 Определение. Суммой нескольких векторов ,
, , ,….,
является вектор
, соединяющий начало первогослагаемого вектора , с концом последнего слагаемого
вектора , при условии, что начало каждого
последующего вектора совмещено с концом
предыдущего.
Правило многоугольника
,
=
+
+
+
+
….
+
Слайд 14
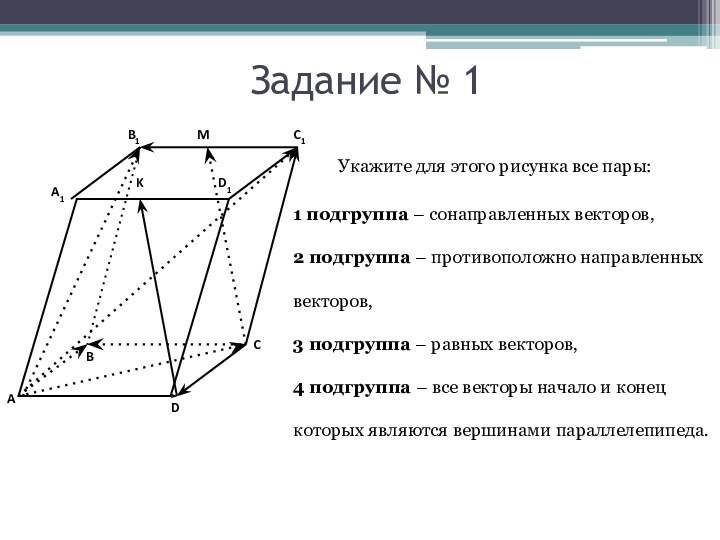
Задание № 1
1 подгруппа – сонаправленных векторов,
2 подгруппа
– противоположно направленных векторов,
3 подгруппа – равных векторов,
4 подгруппа
– все векторы начало и конец которых являются вершинами параллелепипеда.Укажите для этого рисунка все пары:
Слайд 15
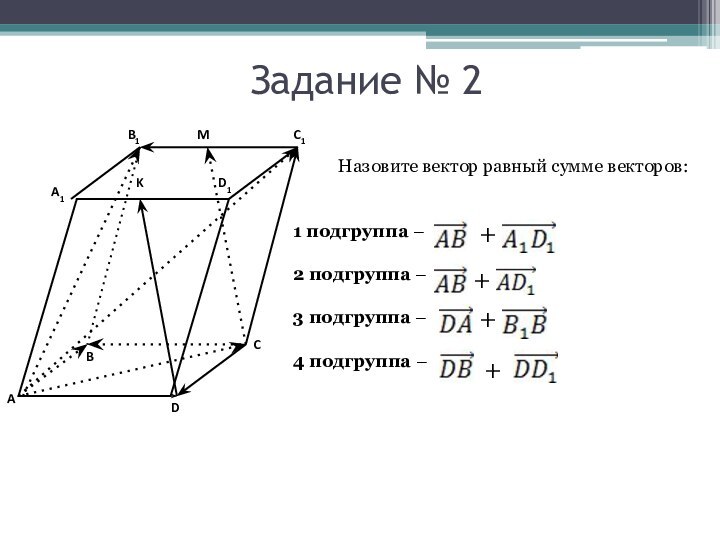
Задание № 2
1 подгруппа –
2 подгруппа –
3 подгруппа –
4 подгруппа –
Назовите вектор равный сумме векторов:
+
+
+
+
Слайд 16
Вопросы:
Что такое вектор?
Что понимают под длинной или модулем
вектора?
Какие векторы называются коллинеарными?
Какие векторы называются сонаправленными?
Какие векторы называют
равными?Как построить сумму двух векторов? Какие правила сложения двух векторов мы сегодня изучили?
Как называется правило сложения более двух векторов?