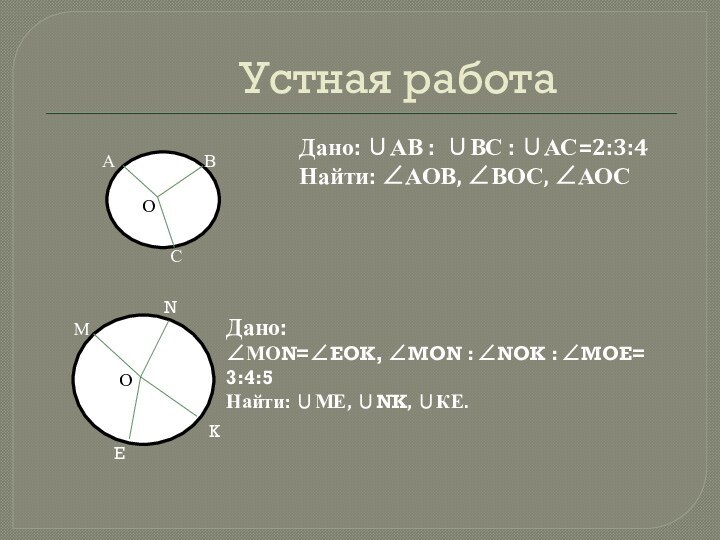
АОВ, ВОС, АОС
Дано:
МОN=EOK, MON : NOK : MOE=
3:4:5Найти: МЕ, NK, КЕ.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть








Вписанный угол
B
O
C
M
A
B
O
C
M
A
O
B
2
1
C
A
A
B
C
D
A
O
B
C
D