- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Задачи о лабиринтах
Содержание
- 2. Происхождение задачи о лабиринтахСлово «лабиринт» — греческое и в переводе означает ходы в подземельях.
- 3. Природные подземные пещерыИскусственные лабиринты
- 4. Лабиринт ДедалаЛабиринты бывают самой разнообразной формы и устройства.
- 5. Во Франции того времени лабиринты выкладывались из
- 6. «Город Троя»Лабиринты в Англии«Следы пастуха» В Англии
- 7. Лабиринты
- 8. «Дерновый» лабиринт (33—34 м в диаметре), просуществовавший
- 9. Леонард Эйлер
- 10. Геометрическая постановка задачи о лабиринтахАллеи, дорожки, коридоры
- 11. Правило 1. Отправляемся от выбранной вершины (первого перекрестка)
- 12. замечания:Выходя из точки отправления, скажем А, мы
- 13. 2. БеседкаА теперь, для вас будет
- 14. Скачать презентацию
- 15. Похожие презентации













Слайд 2
Происхождение задачи о лабиринтах
Слово «лабиринт» — греческое и
в переводе означает ходы в подземельях.
Слайд 5 Во Франции того времени лабиринты выкладывались из камня
или изображались на полу церквей и соборов. Они называлась
большей частью «Путь в Иерусалим» и служили символом трудного земного путешествия «святие места», наградой за которое является небесная благодать, поэтому центр лабиринта часть называли «небом».Лабиринт, выложенный из камня на
полу храма святого Квентина во Франции.
Вход снизу по вертикальной линии
Лабиринт в Шартрском соборе во Франции.
Слайд 6
«Город Троя»
Лабиринты в Англии
«Следы пастуха»
В Англии не
встречаются лабиринты на церковном полу, но зато было очень
много лабиринтов, сделанных из дерна на лужайках. Они носили различные название: «Город Троя»-«Следы пастуха» в т.п. О таких лабиринтах упоминает Шекспир в своих пьесах «Сон в летнюю ночь» и «Буря».
Слайд 8
«Дерновый» лабиринт (33—34 м в диаметре),
просуществовавший до
1797 года в Англии в графстве Эссекс.
Итальянский лабиринт XVI столетия.
Слайд 10
Геометрическая постановка задачи о лабиринтах
Аллеи, дорожки, коридоры и
т. п. лабиринты тянутся, изгибаясь во все стороны, перекрещиваются,
расходятся по всевозможным направлениям, ответвляются, образуют тупики и т. д. мы все перекрестки обозначим просто точками, а все эти аллеи, дорожки, коридоры и т. д. будем принимать просто за линии, прямые или кривые, плоские, или нет - все равно, но эти линии соединяют, наши точки.Эти точки и эти линии вместе составляют геометрическую сеть, или лабиринт, если какая- либо точка, движущаяся по линиям этой сети, может прийти к любой другой точке, не покидая линий нашей системы (или сети).
Приняв это может последовательно описать все линии сети без всяких скачков и перерывов и при этом по каждой линии сети она пройдет ровно два раза. При этом она, конечно же пройдет через точку обозначающую выход из лабиринта.
Возможность обхода следует, вообще говоря, из того, что фигуру, полученную
из сети двоением всех линий, можно описать одним росчерком.
Геометрическая сеть.
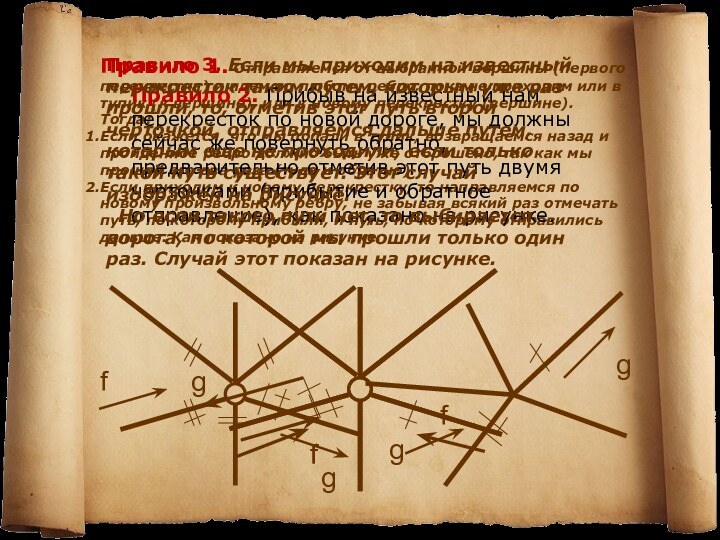
Слайд 11 Правило 1. Отправляемся от выбранной вершины (первого перекрестка) и
идем по любому ребру, пока не приходим или в
тупик (к вершине), или к новому перекрестку (вершине).Тогда:
Если окажется, что мы попали в тупик, возвращаемся назад и пройденное ребро должно быть уже отброшено, так как мы прошли его два раза (туда и обратно).
Если приходим к новому перекрестку, то направляемся по новому произвольному ребру, не забывая всякий раз отмечать путь, по которому прибыли, и путь, по которому отправились дальше. Как показано на рисунке.
f
g
Правило 2. Прибыв на известный нам перекресток по новой дороге, мы должны сейчас же повернуть обратно, предварительно отметив этот путь двумя черточками (прибытие и обратное отправление), как показано на рисунке.
f
g
Правило 3. Если мы приходим на известный перекресток таким путем, которым уже раз прошли, то, отметив этот путь второй черточкой, отправляемся дальше путем, которым еще не проходили, если только такой путь существует. Этот случай изображен на рисунке.
Но если такого пути нет, то выбирается дорога, по которой мы прошли только один раз. Случай этот показан на рисунке.
g
g
f
f
Слайд 12
замечания:
Выходя из точки отправления, скажем А, мы ставим
начальный знак (поперечную черточку).
Прохождение через перекресток по одному из
предыдущих трех правил каждый раз добавляет два знака (две поперечные черточки) на линиях, которые сходятся в этой точке;В любой момент прохождения, лабиринта, перед прибытием на какой-либо перекресток или после отправления из него, начальный перекресток (пункт отправления) имеет нечетное число знаков (черточек), а всякий другой перекресток имеет их четное число.
В любой момент, до или после прохода через перекресток, начальный перекресток имеет только один путь, обозначенный только одной черточкой. Всякий же иной из посещенных
уже перекрестков может иметь только два пути, обозначенных одной черточкой.
5. После полного обхода лабиринта у всех перекрестков все пути должны иметь по две черточки» Это, впрочем, входит прямо в условие задания.
1. Головоломный лабиринт
Приведем один не построенный, а только начерченный лабиринт (рис. 1
с готовым и упрощенным решением его: все тупики (слепые проходы) в нем уже заштрихованы, и главнейшие пути указаны точечными или штриховыми линиям. И по решению, данному на этой фигуре, видно, что от А надо сначала идти к С и потом от F к В, но, когда мы придем к С, у нас появляются три дороги, обозначенные 1, 2, 3, чтобы, дойти до D, Точно так же, когда мы дойдем до Е, тоже видны три дороги, обозначенные 4, 5, 6, чтобы дойти до F. У нас есть также обозначенная точками дорога от С до Е, другая—обозначенная точками дорога от D до F и проход от D до Е, указанный звездами. Мы можем, следовательно, выразить положение дела маленькой упрощенной диаграммой на рис. 2.
Здесь , все пути соответствуют путям кругообразного лабиринта, но только более доступны глазу.
A
C
D
E
F
B
рис. 2
Слайд 13
2. Беседка
А теперь, для вас будет нетрудно
найти путь к беседке, расположенной в парке, изображенном на
рисунке. Быть может, для сокращения времени вам не бесполезен, будет совет начать поиски от – хижины и найти лучше выход из этого коварного парка, чем начинать с входа. Впрочем, при наличии свободного времени это безразлично.3. Еще лабиринт
Вот ещё любопытный образчик лабиринта, в котором надо пробраться по кратчайшей дороге к центру рисунке.