анатома и морфолога Ewald R. Weibel в свою лабораторию
в США.
André F. Cournand и Dickinson W. Richards, получили в 1956 г. Нобелевскую премию по физиологии за фундаментальные работы по легочному кровообращению.
+
Кардиолог и математик Доминго М. Гомез, получил приют у André F. Cournand после бегства в США от кубинской революции Фиделя Кастро
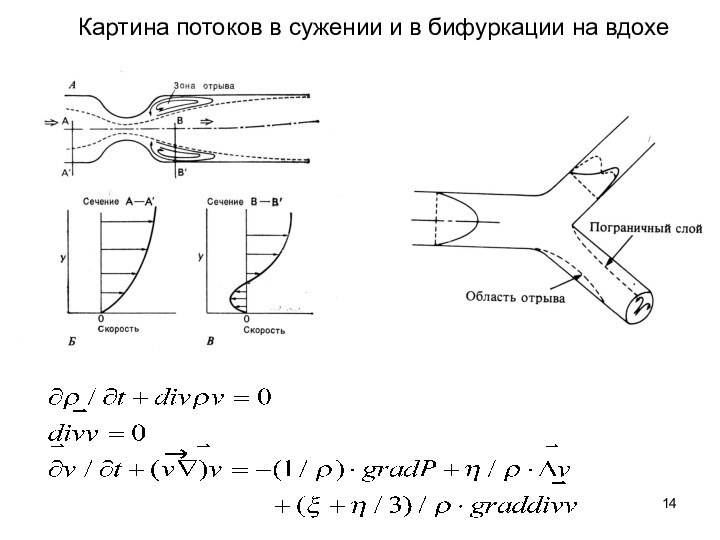
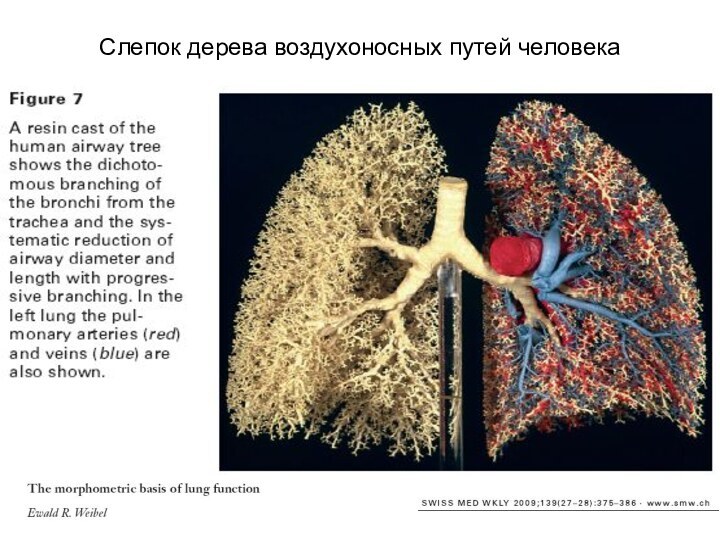
Они разработали методы анализа и по плоским срезам восстановили пространственную картину структуры легких.
Первая крупная работа по геометрии с применением мат.методов –
Weibel ER. Morphometry of the Human Lung. Springer Verlag and Academic Press, Heidelberg-New York 1963.
Е. Вейбель - «Морфометрия легких человека» - М., 1970.
Способствовало появлению новых применений математики в биологии.
Стереология – наука о том, как по плоским срезам восстановить пространственную картину с учетом нерегулярностей структуры. .
Применение фракталов в биологии и медицине.
2005
Ewald R. Weibel

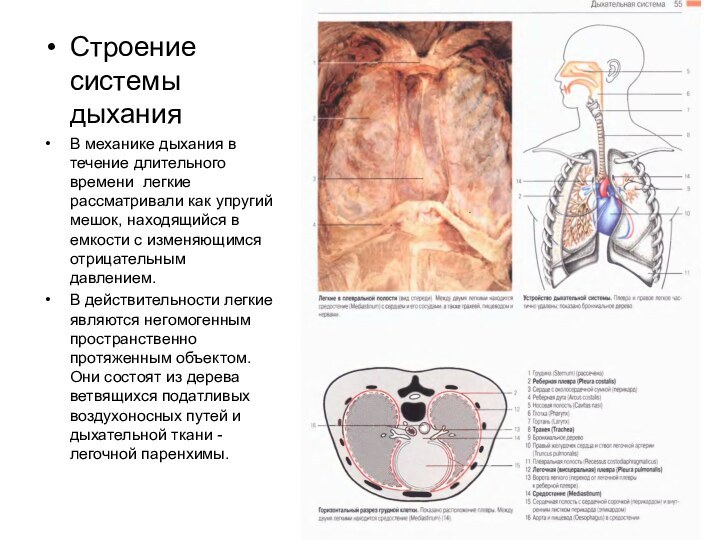






![Функции и строение легких, механика дыхания Модель правильного симметричного дихотомического ветвления дыхательных путей человека [Вейбель Р., 1970]](/img/tmb/15/1472756/3ab02e1d02cfa34fd51c0b65367291a3-720x.jpg)