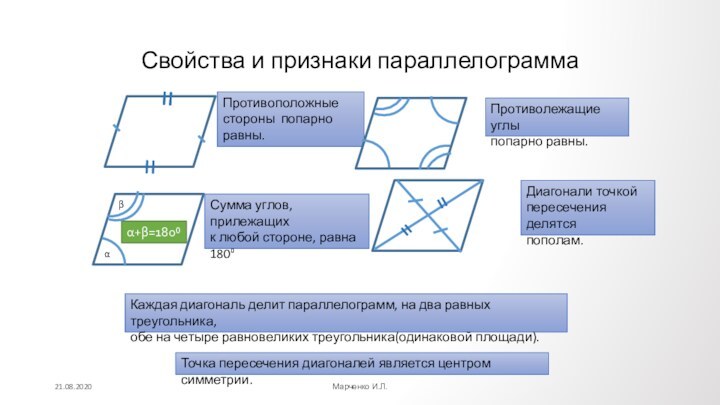
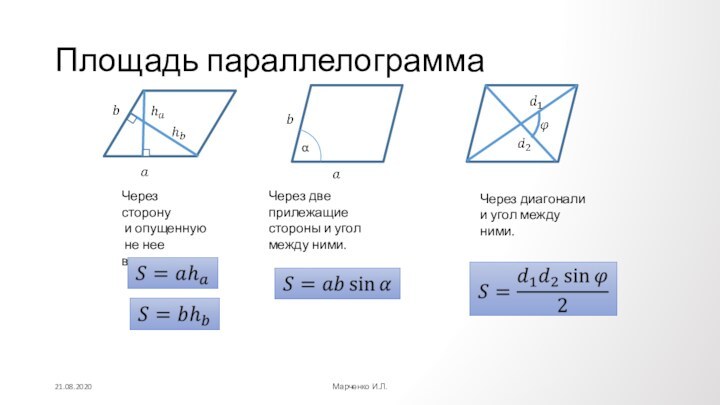
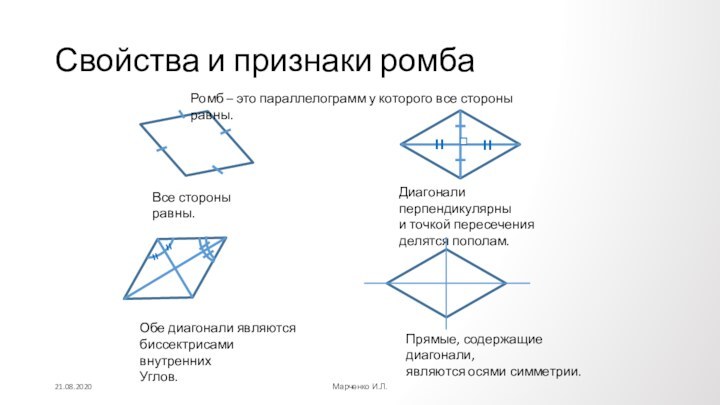
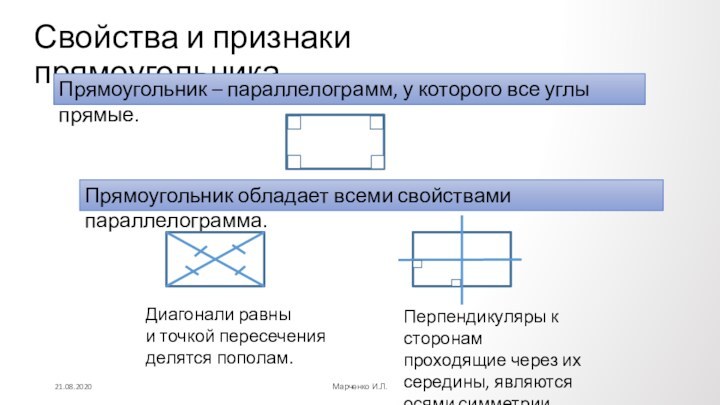
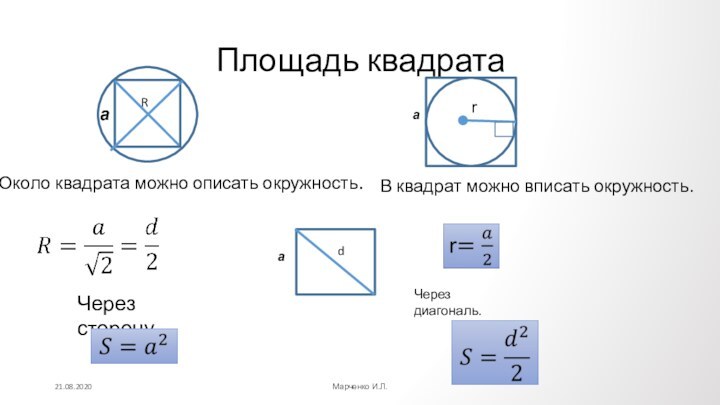
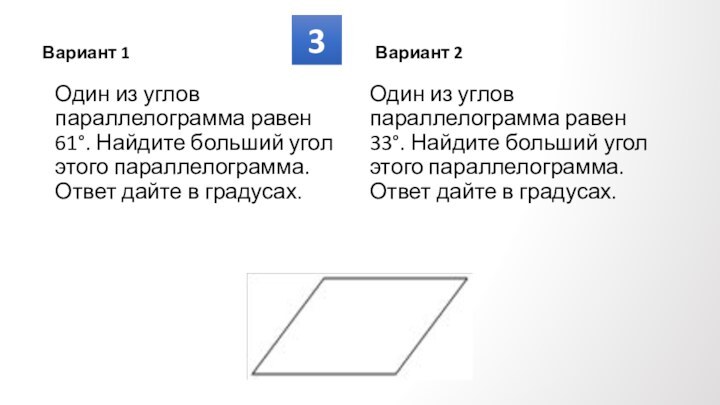
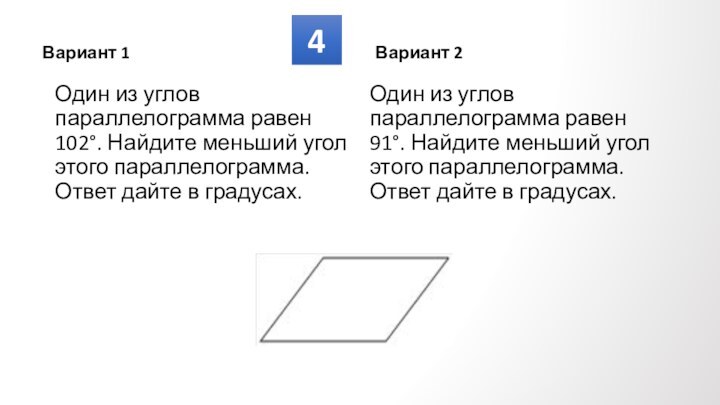
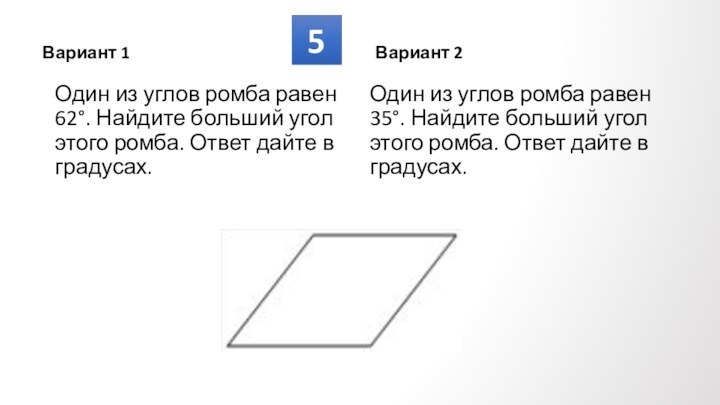
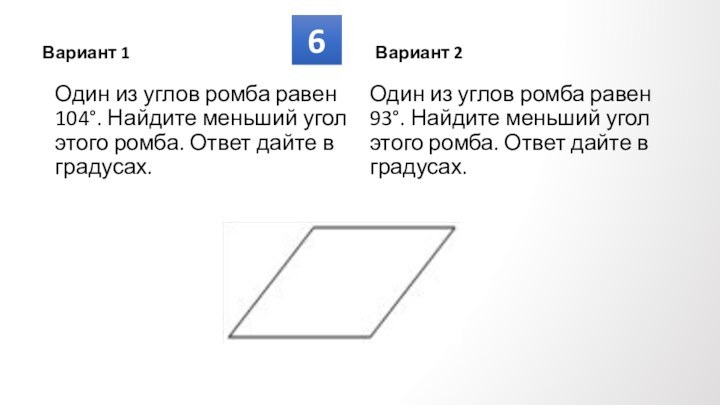
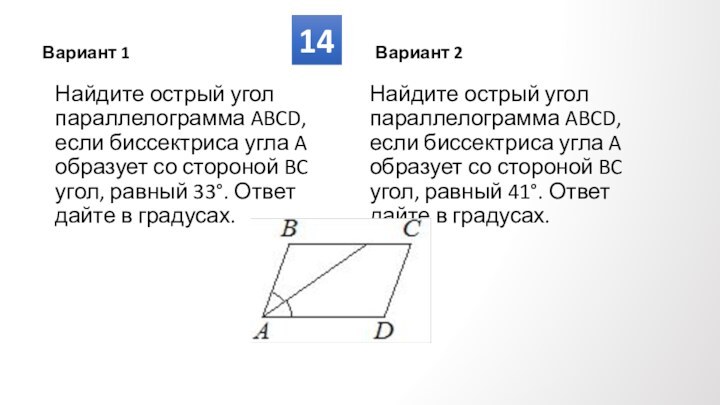
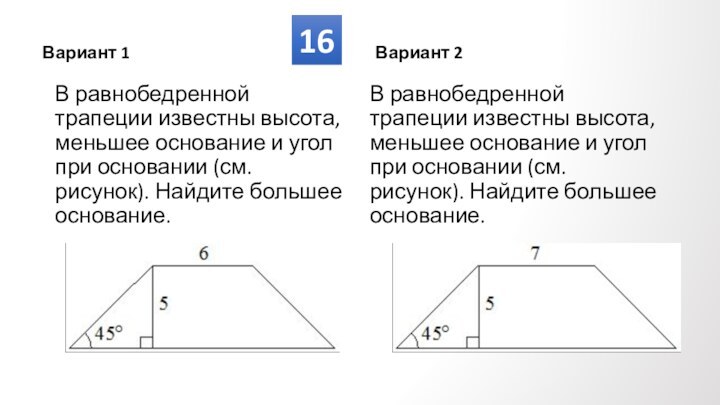
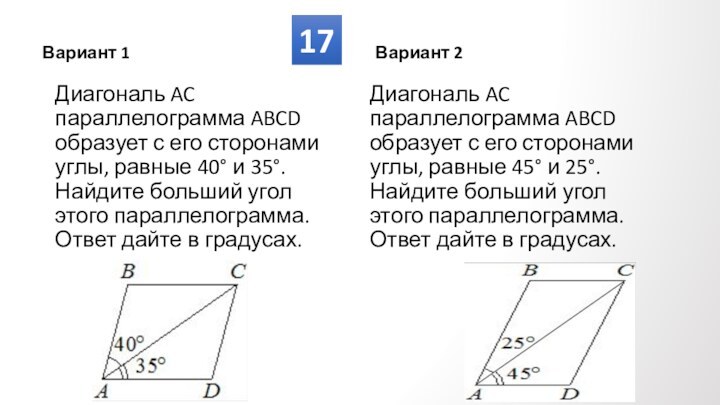
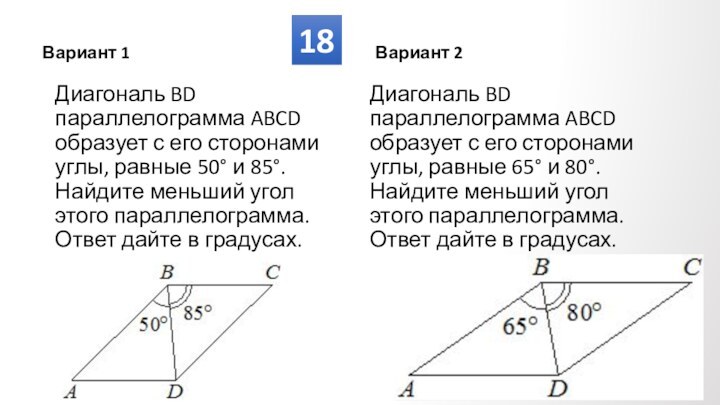
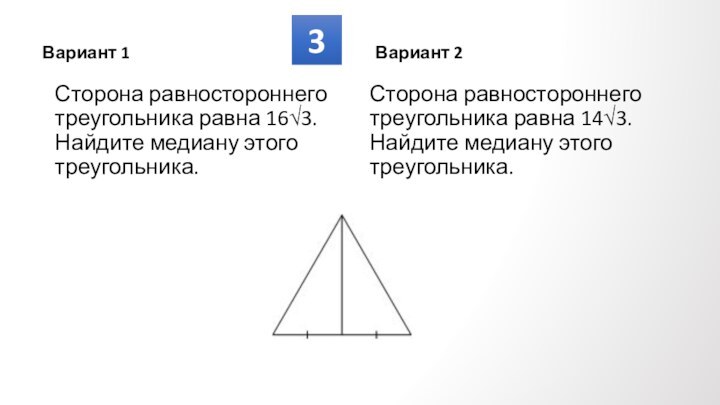
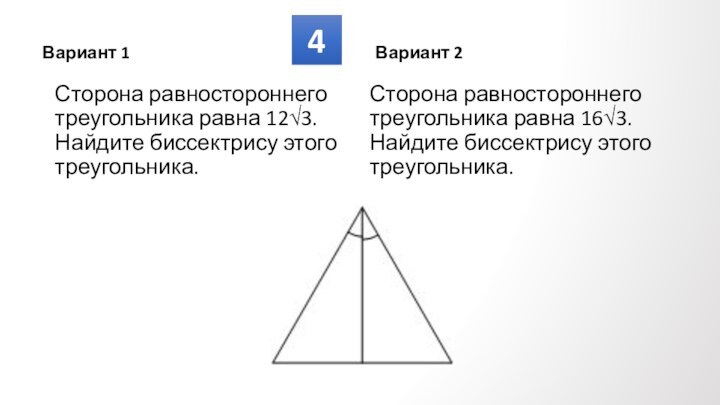
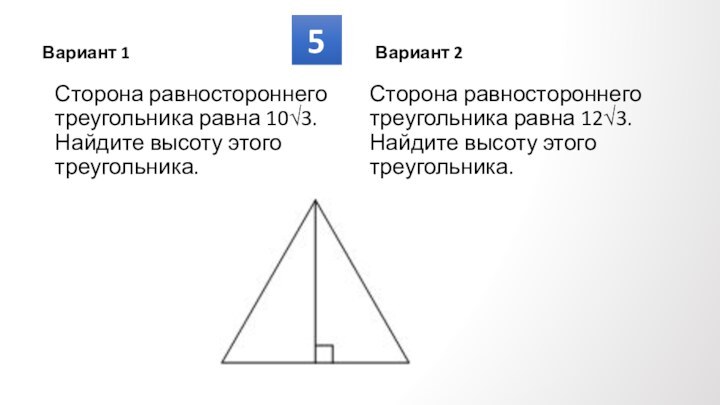
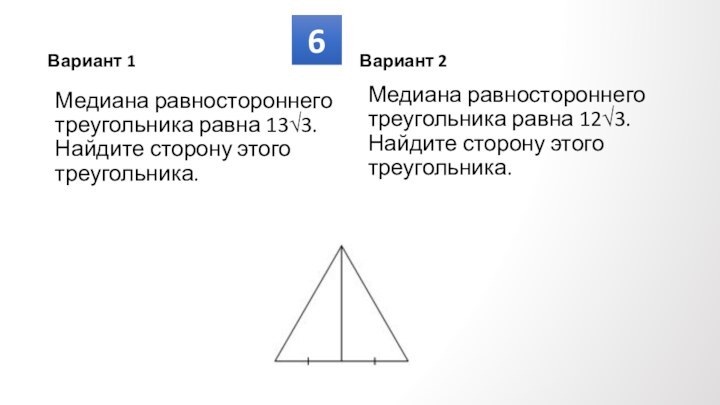
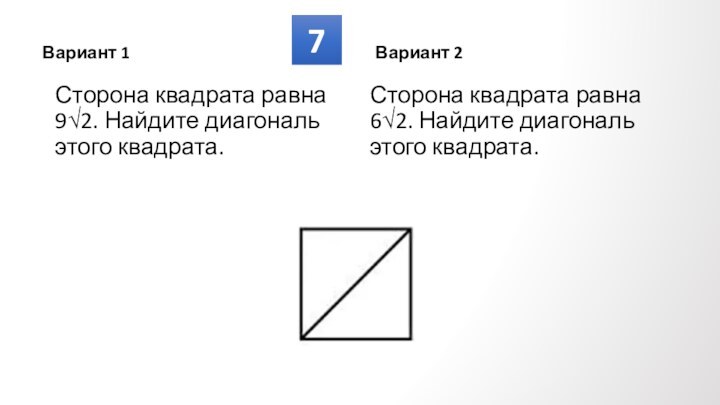
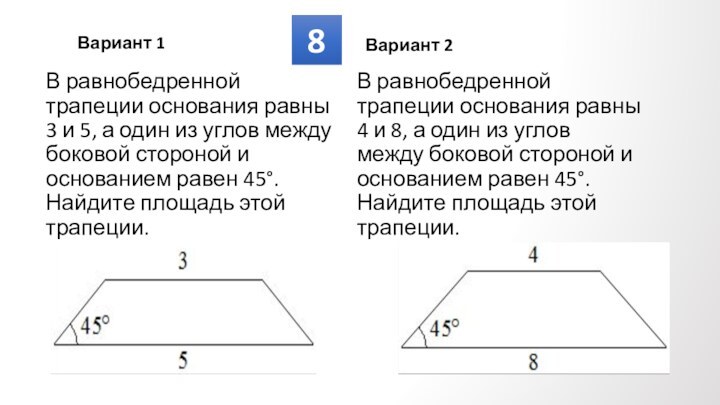
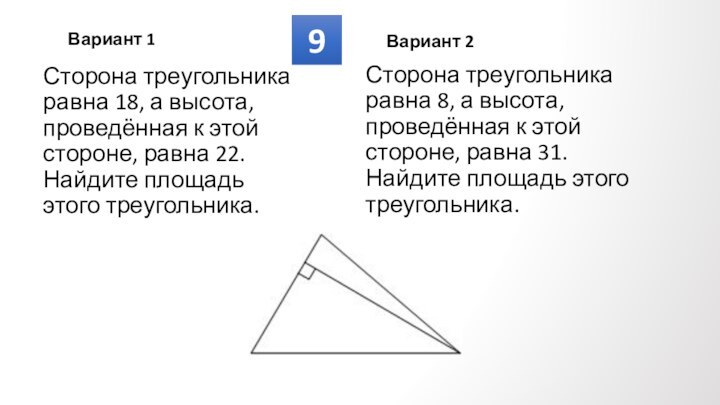
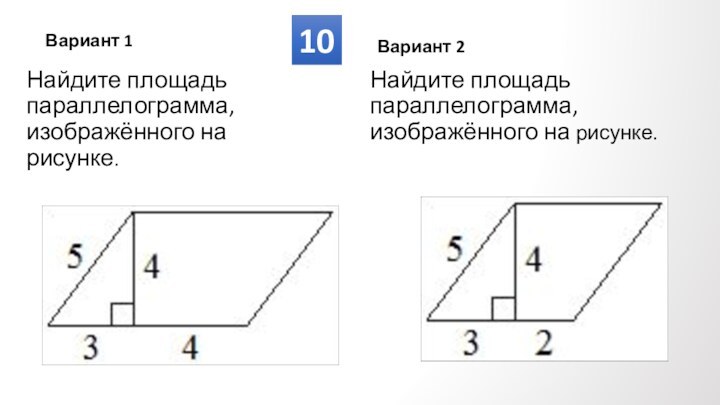
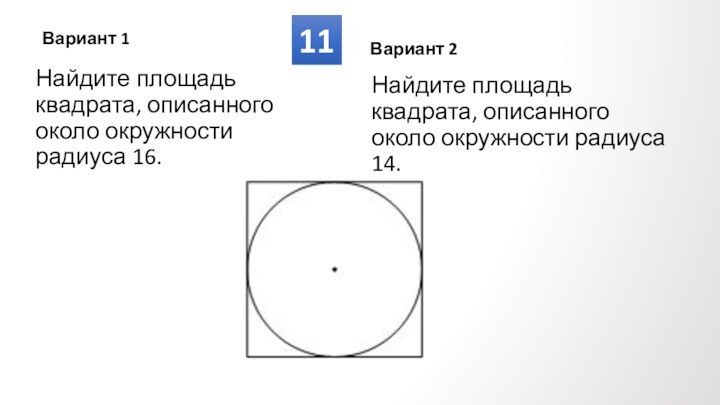
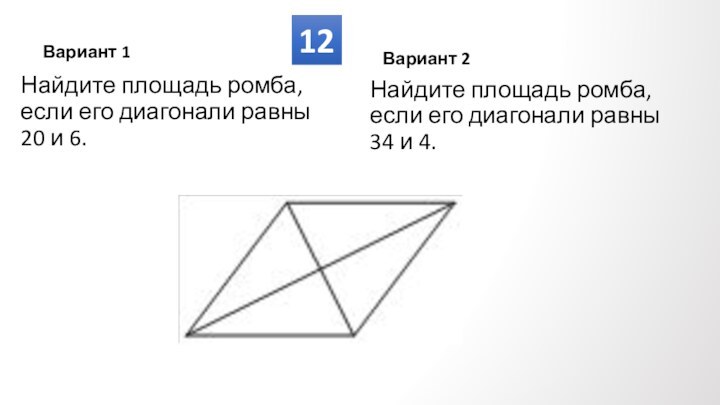
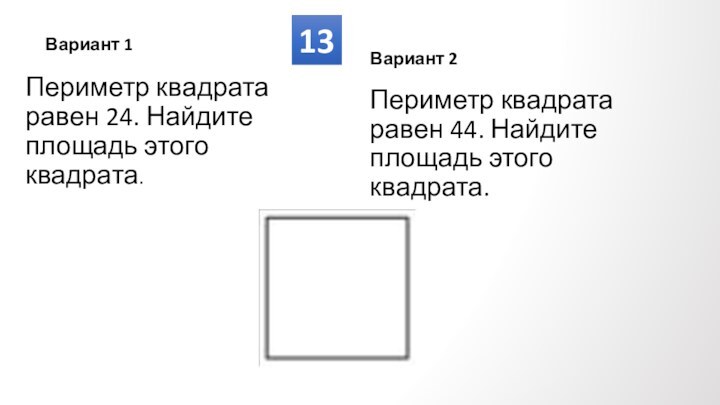
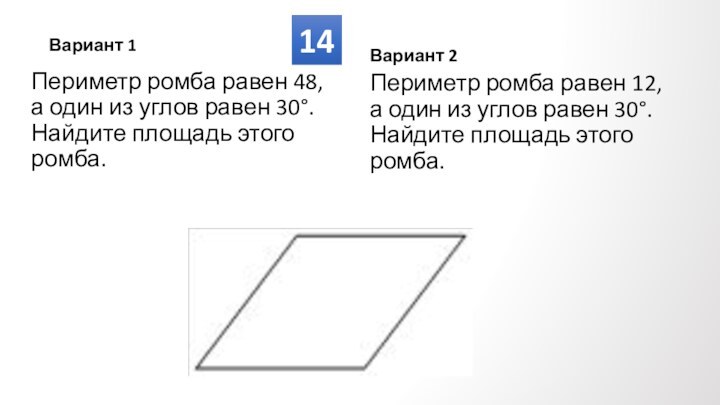
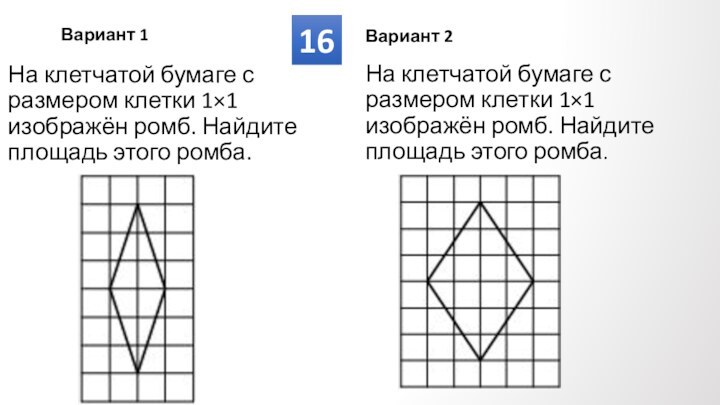
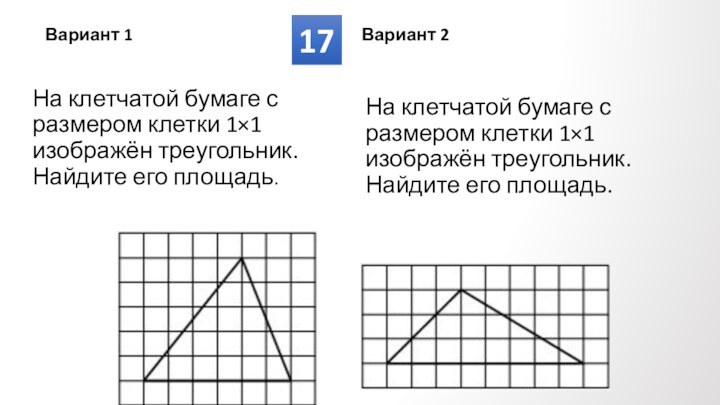
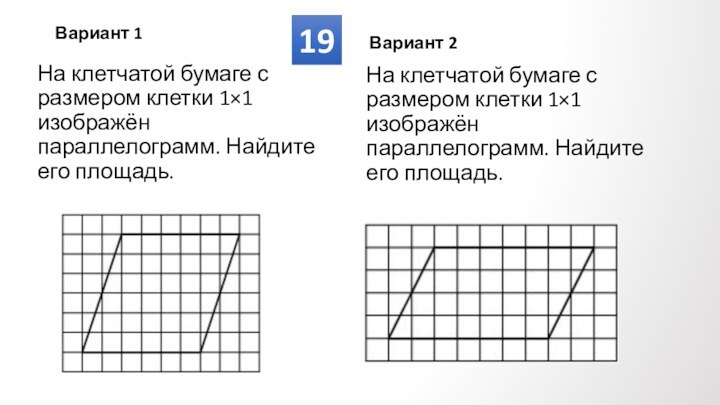
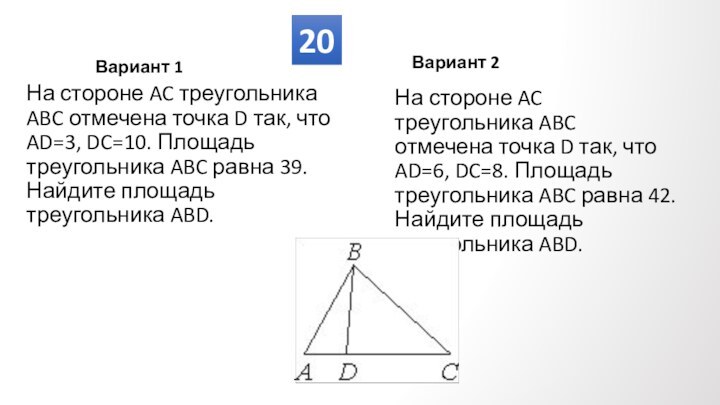
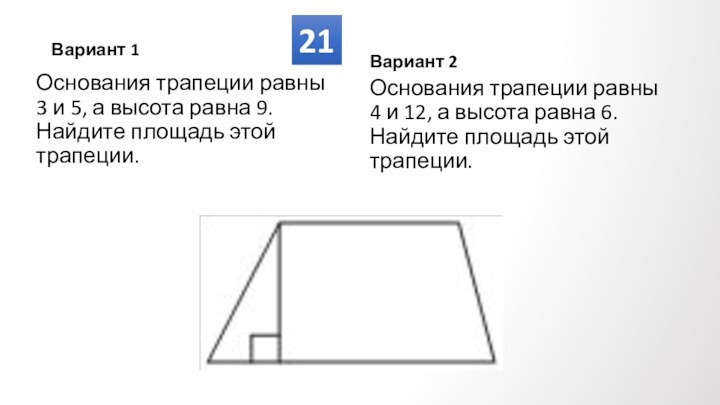
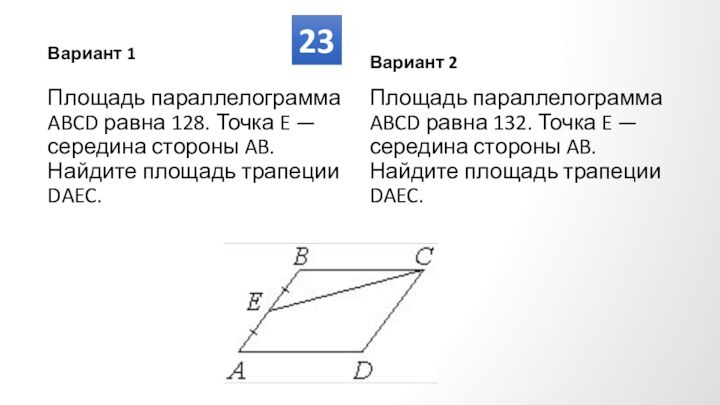
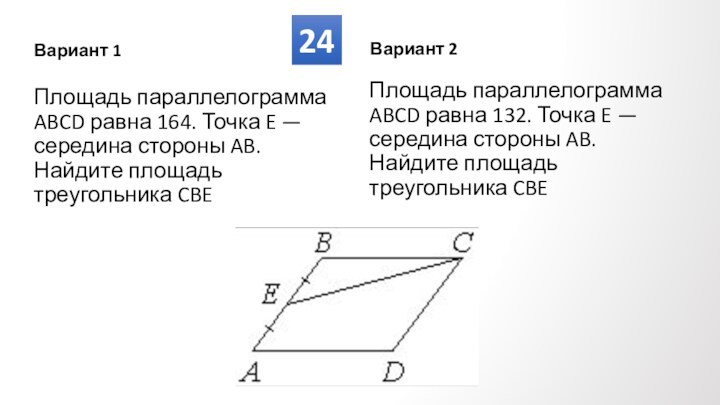
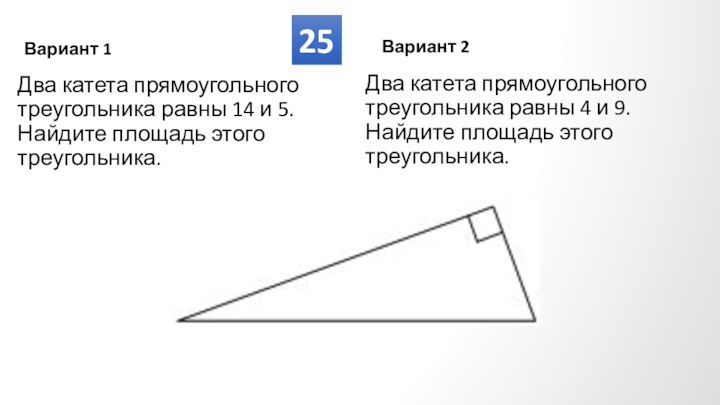
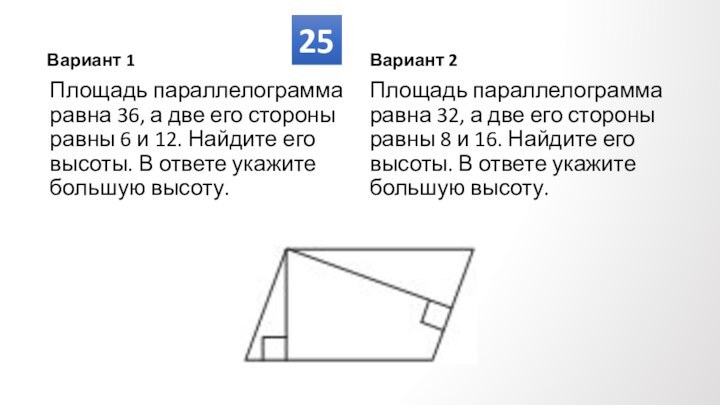
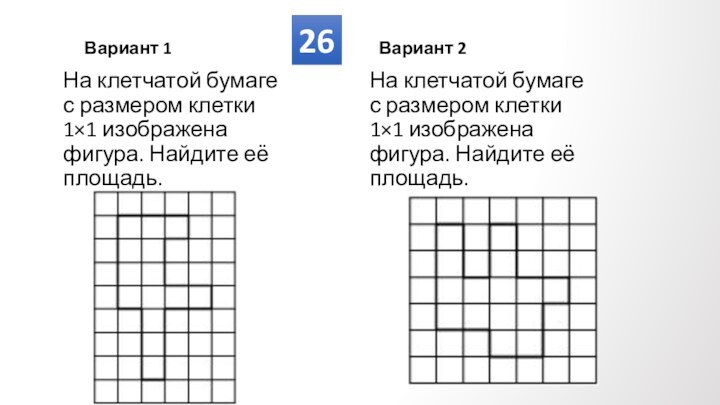
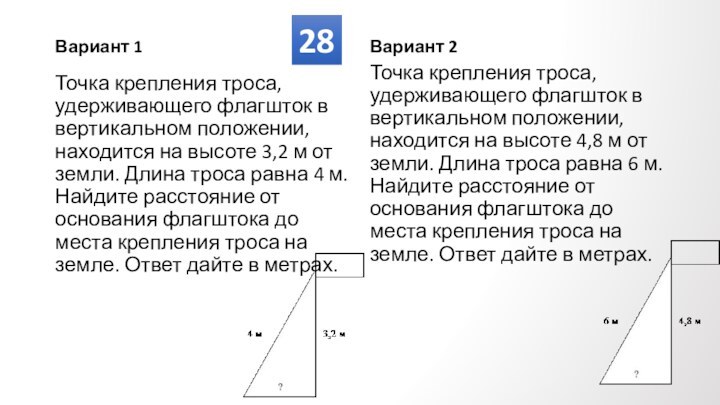
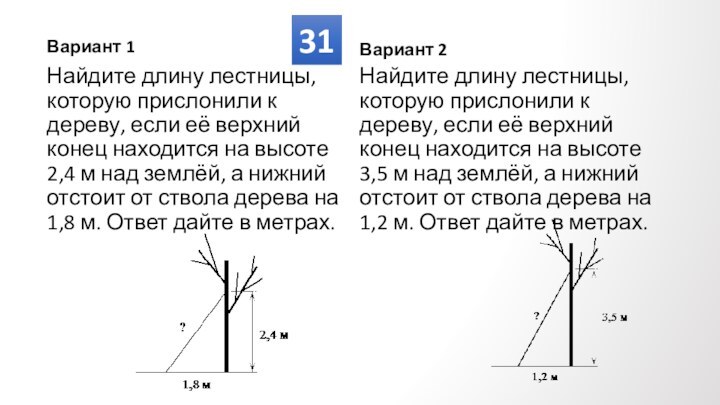
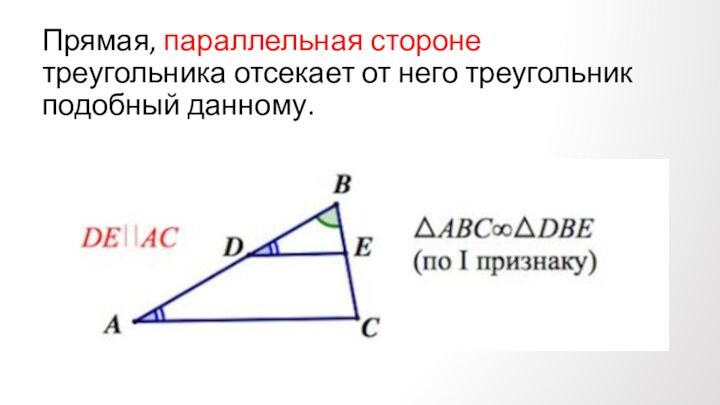
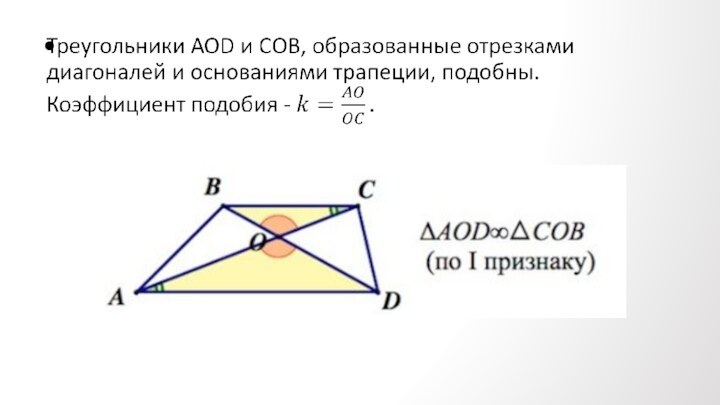
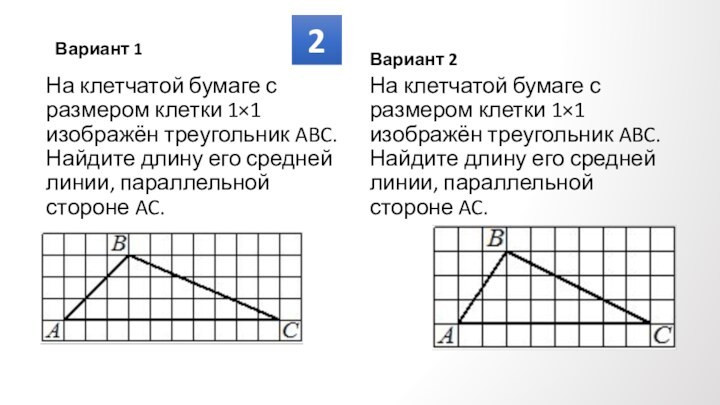
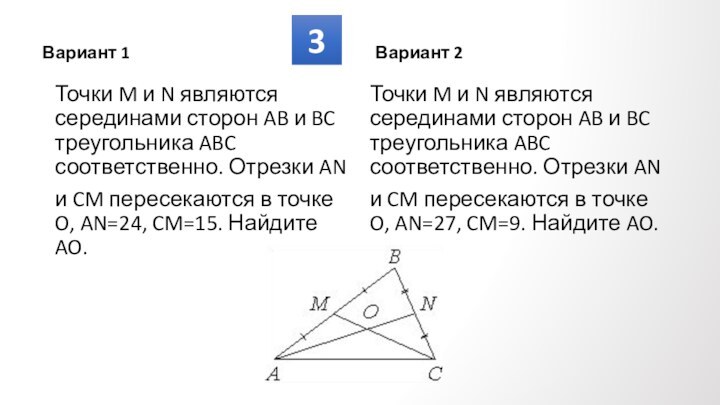
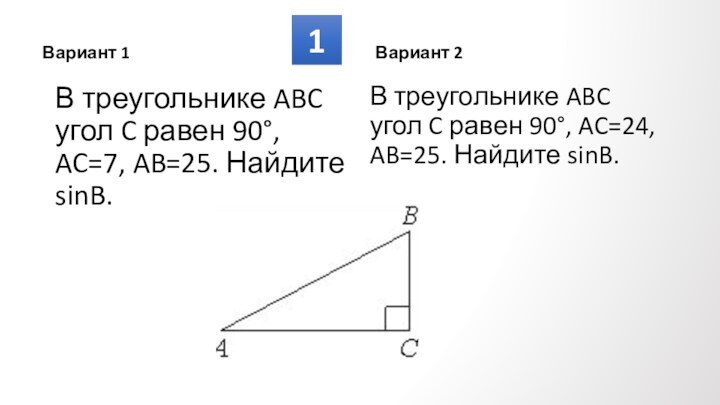
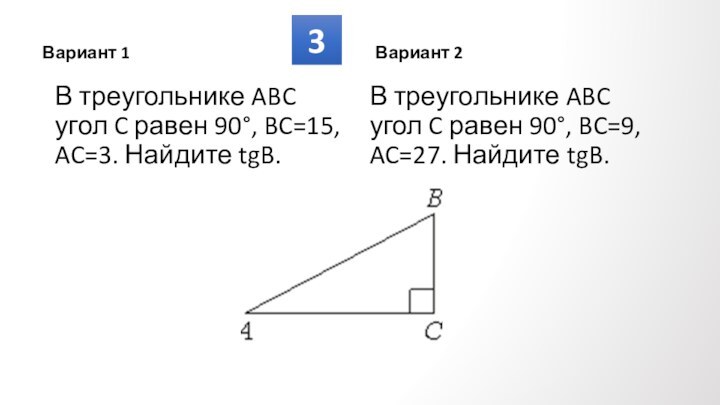
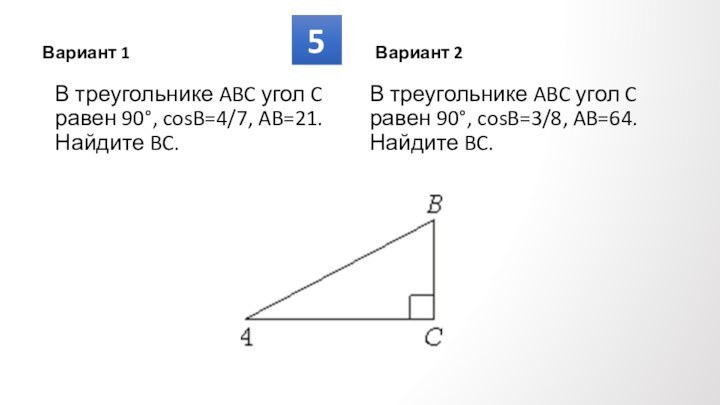
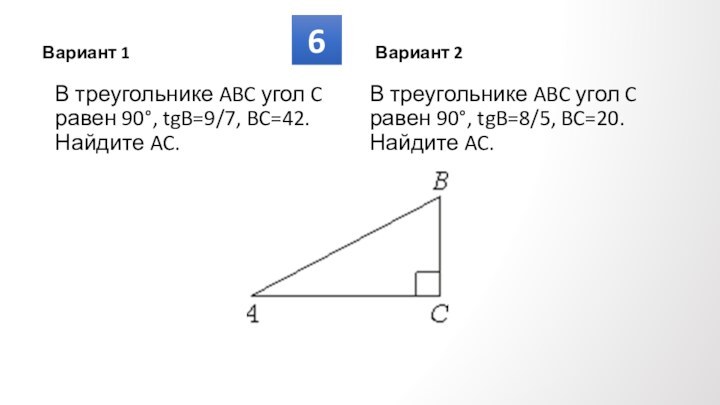
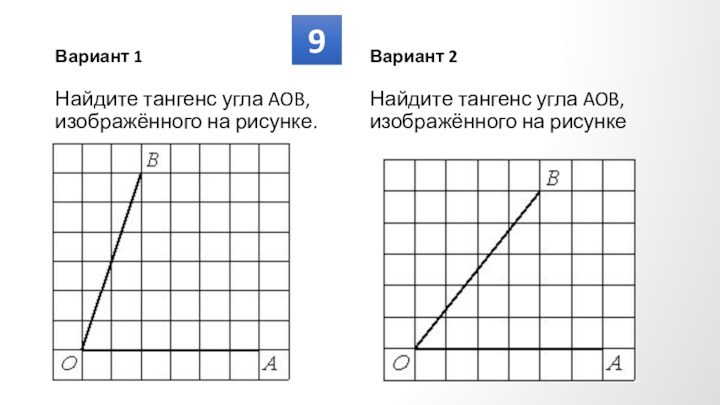
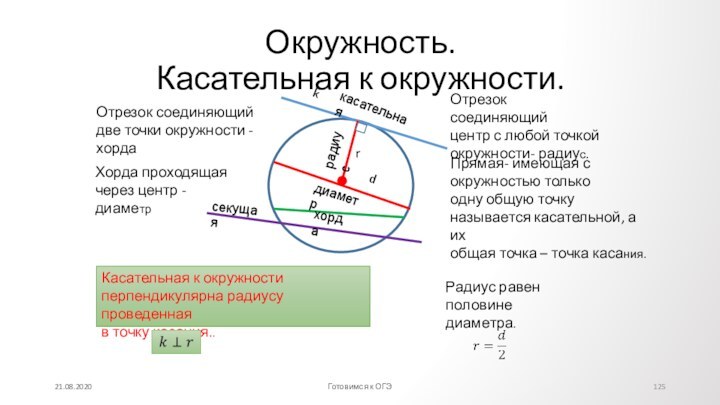
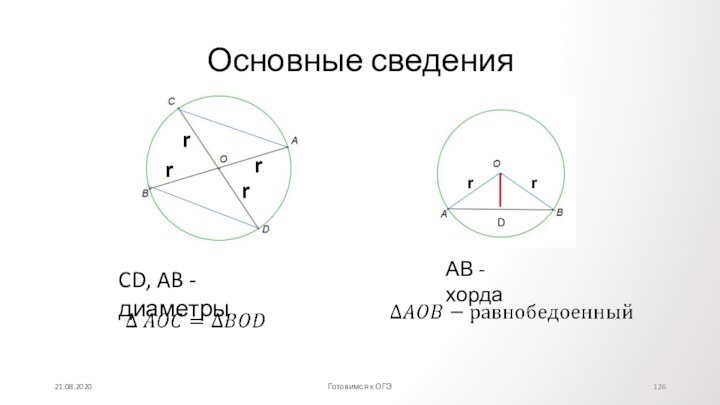
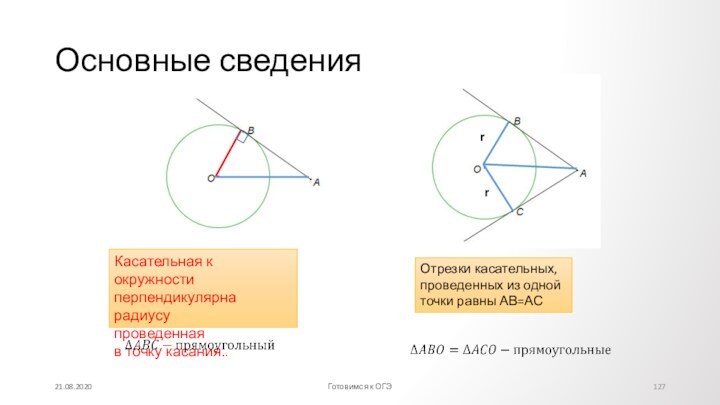
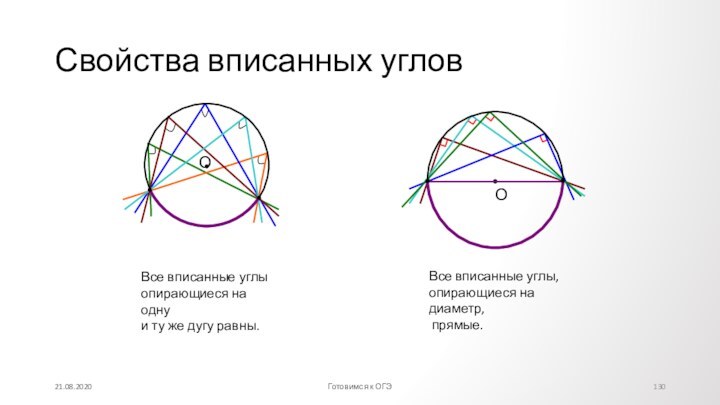
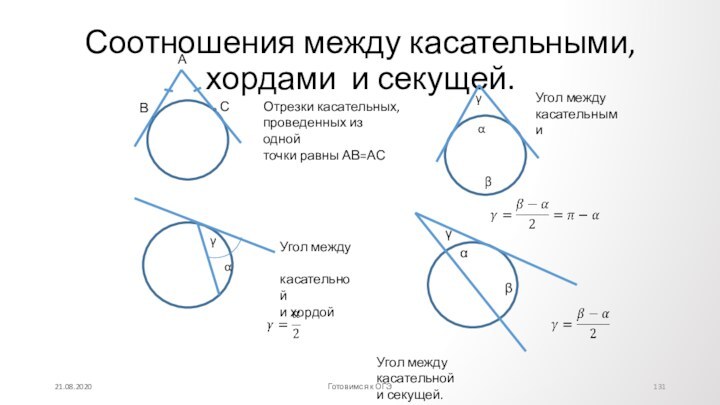
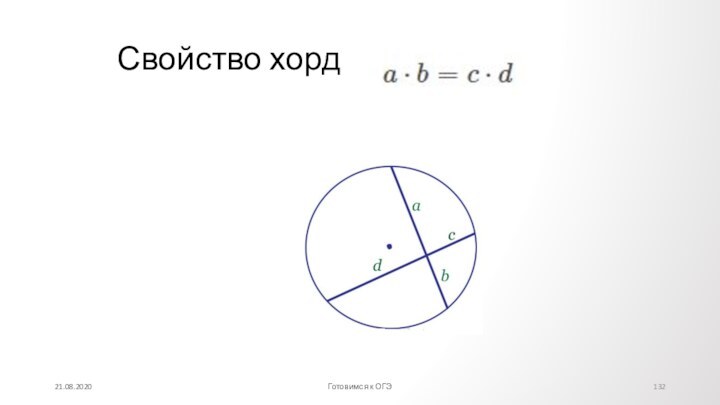
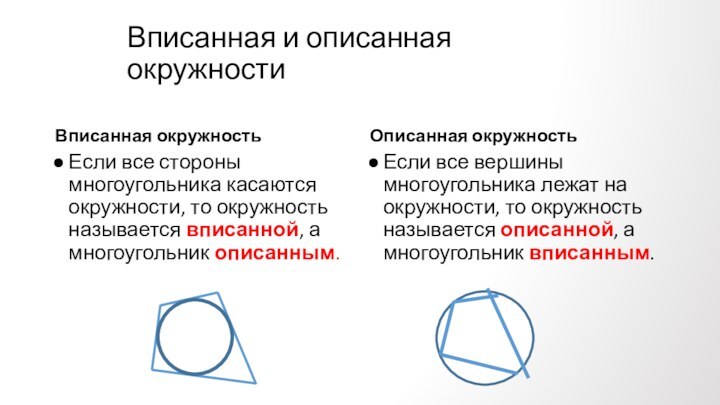
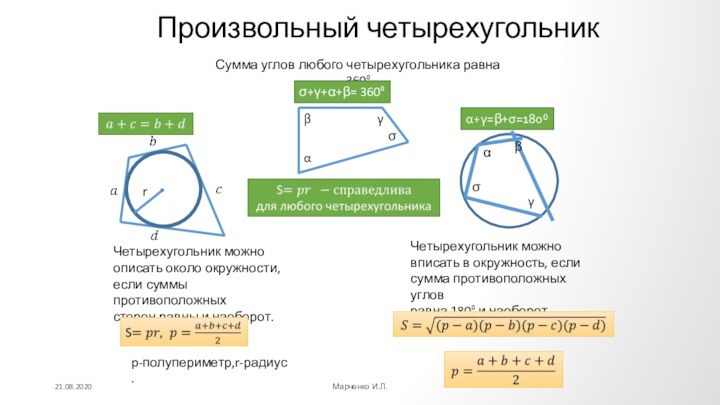
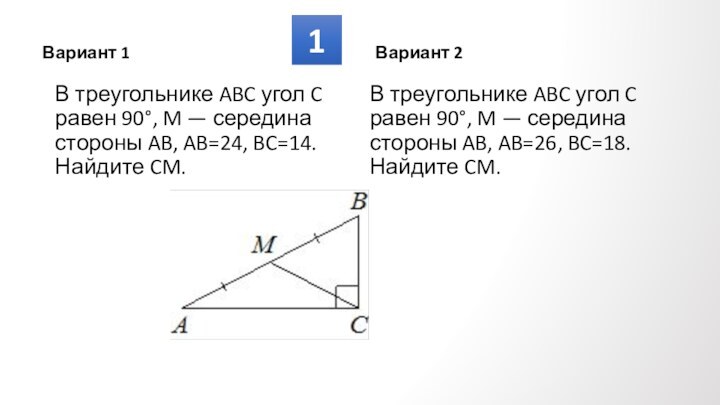
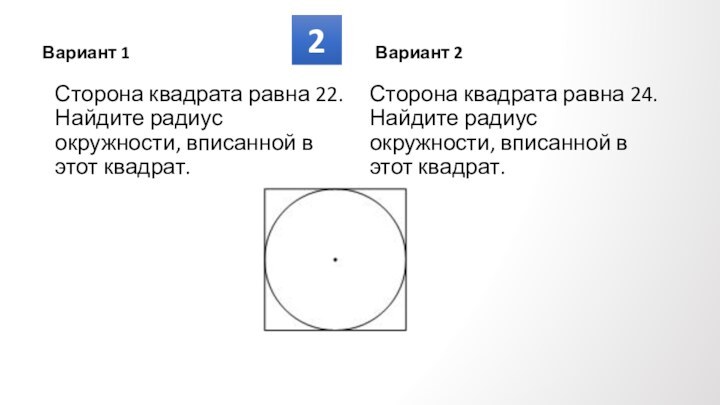
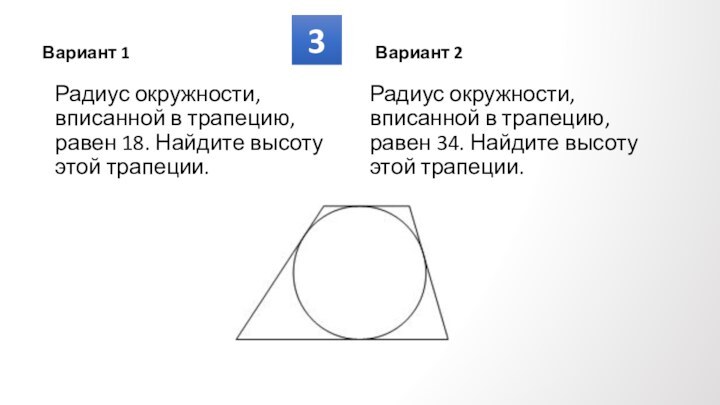
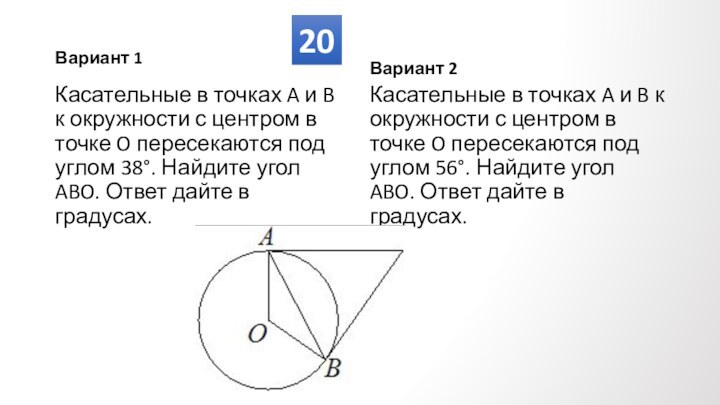
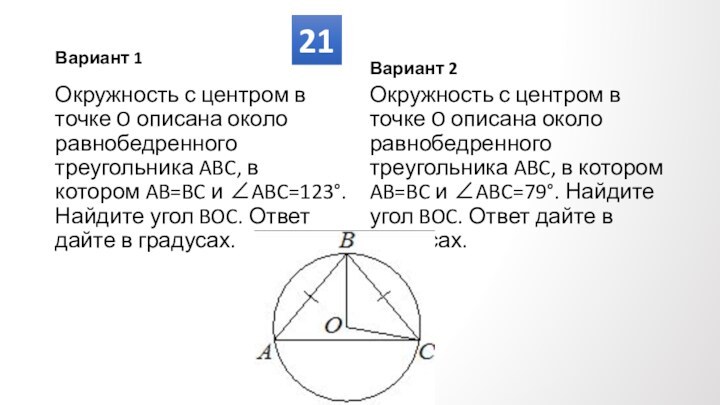
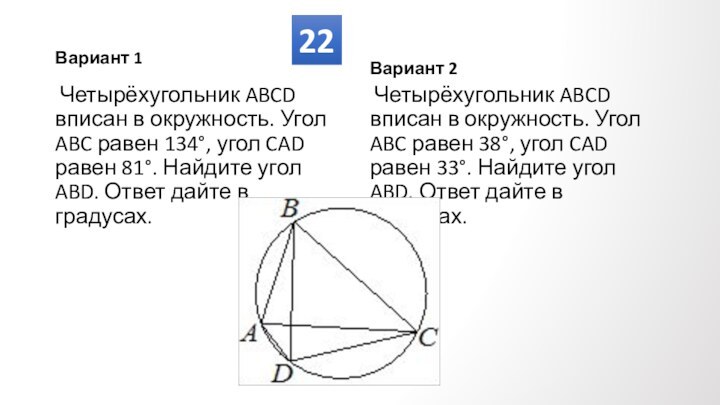
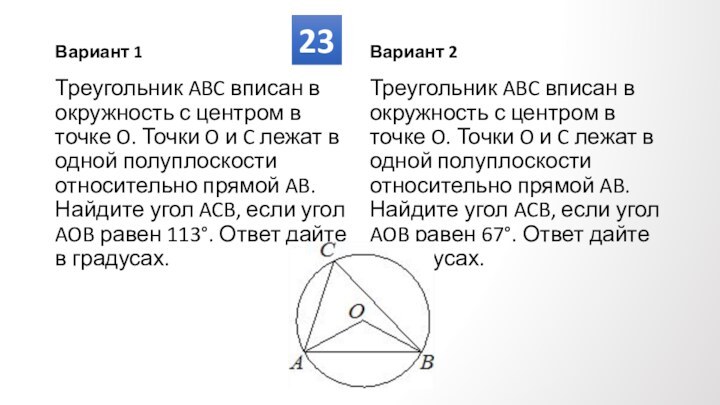
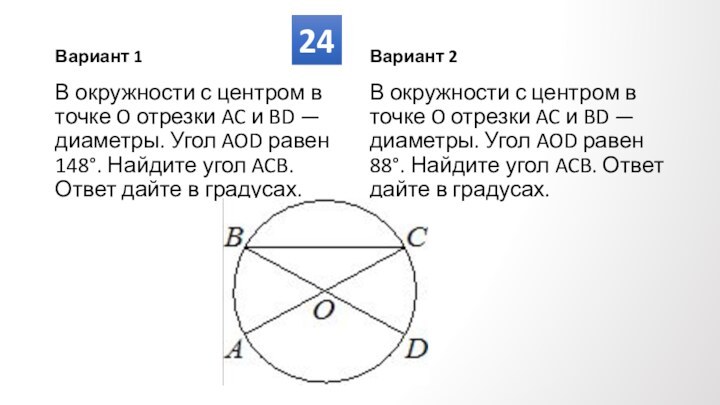
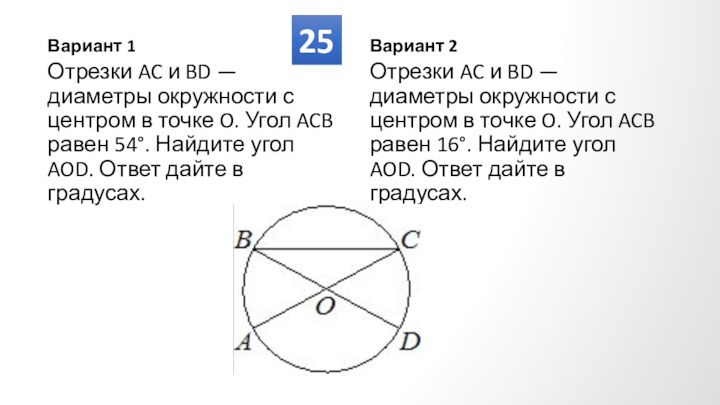
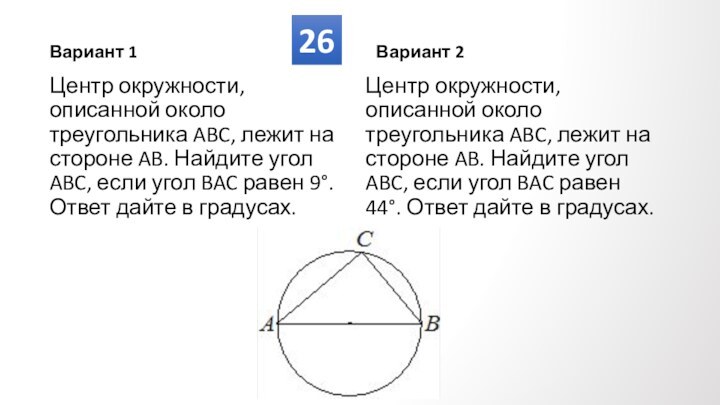
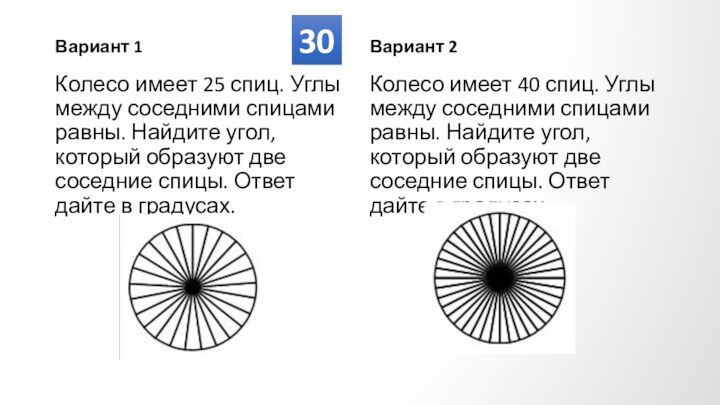
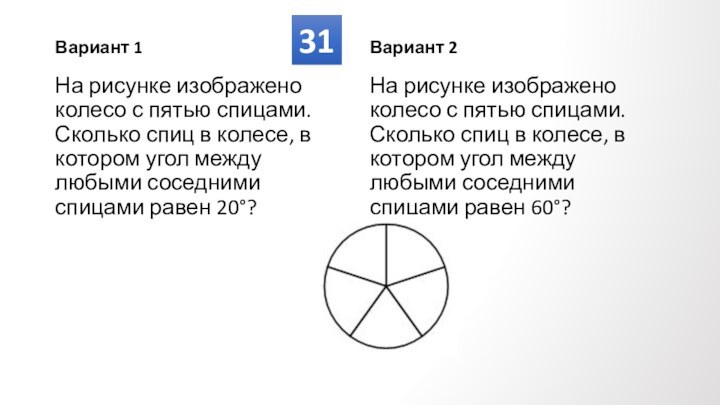
Противолежащие углы
попарно равны.
Сумма углов, прилежащих
к любой стороне, равна
180⁰
α
β
α+β=180⁰
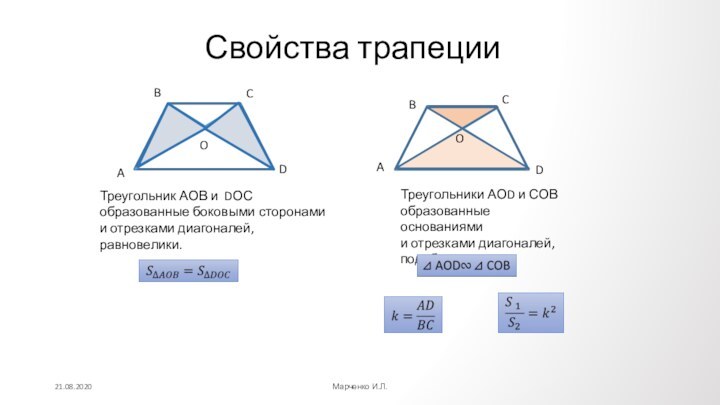
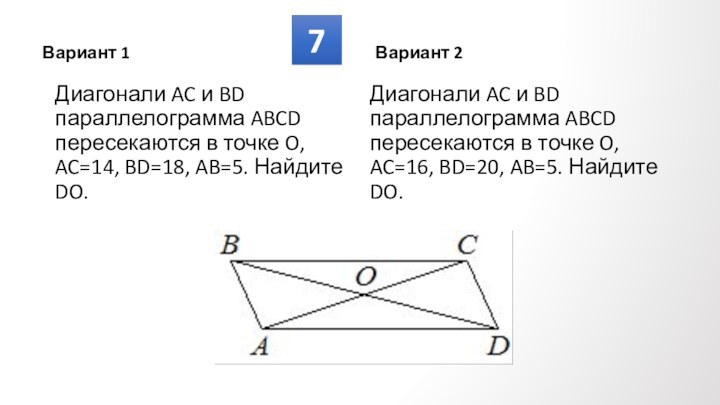
Диагонали точкой
пересечения
делятсяпополам.
=
Каждая диагональ делит параллелограмм, на два равных треугольника,
обе на четыре равновеликих треугольника(одинаковой площади).
Точка пересечения диагоналей является центром симметрии.