Слайд 2
Решите одну задачу (по выбору)
Однажды в Стране Чудес
Королева Червей устроила прием. Она приготовила 100 пирожков и
раздала каждому фавориту по 9 пирожков, а каждому из остальных гостей – по 5 пирожков. Сколько фаворитов и сколько остальных гостей было на приеме?
Докажите, что а = 1, если:
Сколько существует чисел вида abcabc, которые кратны 13?
Слайд 3
ФГОС НОО
Метапредметные результаты освоения ООП начального общего
образования
…
10) овладение логическими действиями сравнения, анализа, синтеза, обобщения, классификации
по родовидовым признакам, установления аналогий и причинно-следственных связей, построения рассуждений, отнесения к известным понятиям;
11) готовность слушать собеседника и вести диалог; готовность признавать возможность существования различных точек зрения и права каждого иметь свою; излагать свое мнение и аргументировать свою точку зрения и оценку событий;
…
Слайд 4
ФГОС ООО
Метапредметные результаты освоения ООП основного общего образования
…
6. Умение определять понятия , создавать обобщения, устанавливать аналогии,
классифицировать, самостоятельно выбирать основания и критерии для классификации, устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и делать выводы;
…
Слайд 5
Средство достижения основных результатов ООП –
Формирование универсальных
учебных действий
?
Личностные УУД
Коммуникативные УУД
Познавательные УУД
Регулятивные УУД
общеучебные,
логические,
постановка и
решение проблемы
Слайд 6
Логические ПОЗНАВАТЕЛЬНЫЕ УУД
анализ объектов с целью выделения признаков
(существенных, несущественных)
синтез – составление целого из частей, в том
числе самостоятельное достраивание с восполнением недостающих компонентов;
выбор оснований и критериев для сравнения, сериации, классификации объектов;
подведение под понятие, выведение следствий;
установление причинно-следственных связей, представление цепочек объектов и явлений;
построение логической цепочки рассуждений, анализ истинности утверждений;
доказательство;
выдвижение гипотез и их обоснование.
Слайд 7
Возможности для формирования УУД
Слайд 8
Возможности для формирования УУД
Слайд 9
Трудности
в усвоении доказательств
в начале изучения систематического курса геометрии
Слайд 10
Трудности в усвоении доказательств в начале изучения систематического
курса геометрии
. А
. С
. В
Слайд 11
Учащиеся сталкиваются
с обилием доказательств, которые «вынуждены заучивать,
не понимая еще необходимости доказательства и идеи самого доказательства»
А.
А. Столяр (1919–1993)
Слайд 12
Трудности в усвоении доказательств в начале изучения систематического
курса геометрии
Учащиеся:
Не осознают необходимости обоснования.
Не понимают сущности
доказательства.
Не владеют способами и методами доказательства.
Не имеют собственного опыта в проведении доказательств
…
Слайд 13
Почему геометрию начинают изучать в 7 классе?
К
12–13 годам у учащихся складываются определенные
логические структуры
(Ж. Пиаже)
Слайд 15
«Успешность в овладении логическими действиями определяется не возрастом
субъекта, а типом обучения, в рамках которого эти приемы
усваиваются»
Н. А. Подгорецкая
Слайд 16
«В стихийных условиях обучения правильное логическое мышление формируется
не у всех, очень медленно и с большими огрехами»
В.
В. Давыдов
Слайд 17
Этапы в обучении доказательству
1–4 классы
5–6 классы
7 класс
8–11 классы
Слайд 18
Этапы в обучении доказательству
1–4 классы
5–6 классы
7 класс
8–11 классы
Подготовительный
этап
Слайд 19
Задачи подготовительного этапа
?
Слайд 20
Трудности в усвоении доказательств в начале изучения систематического
курса геометрии
Учащиеся:
Не осознают необходимости обоснования.
Не понимают сущности
доказательства.
Не владеют способами и методами доказательства.
Не имеют собственного опыта в проведении доказательств
…
Слайд 21
Задачи подготовительного этапа
Воспитывать потребность в обосновании суждений.
Формировать правильные представления о сущности доказательства.
Познакомить с основными
способами доказательства.
Обеспечить накопление обучающимися собственного опыта в проведении доказательств.
Слайд 22
«… вообще нужно много упражняться, чтобы научиться какому-либо
виду деятельности, будь то работа напильником, ходьба на лыжах
или логические рассуждения»
А. Д. Александров
Слайд 23
Способы обоснования суждений на уроках математики в начальной
школе
При изучении вопросов:
Сравнение чисел в подготовительный период (сравните числа
2 и 3).
Переместительное свойство сложения (умножения).
Свойство противолежащих сторон прямоугольника.
Сравнение числовых выражений (является ли верным:
а) равенство (60 + 40) : 5 = 60 : 5 + 40 : 5;
б) неравенство 26 ⋅ 5 > 600 : 5).
Решение уравнений (х + 25 = 36)
Решение задач (На верхней полке 18 книг, на нижней – 12. На сколько больше книг на верхней полке, чем на нижней?)
Слайд 24
Математические способы обоснования суждений
Слайд 25
Способы обоснования суждений
Существуют ли в русском языке слова,
в которых три гласные буквы стоят подряд?
Верно ли, что
все треугольники имеют прямой угол?
Является ли неравенство • + • ≤ 18 верным на множестве однозначных натуральных чисел?
Можно ли подобрать числа так, чтобы равенство
***5 + 3**7 · 9*1 = ******3 было верным?
Сумма четных чисел четна. Обоснуйте!
Слайд 26
Математические способы обоснования суждений
Слайд 27
Структура доказательства
тезис;
основания (или аргументы) доказательства;
способ доказательства (демонстрация).
Слайд 28
Правила вывода
Заключения: А(х)→В(х), А(а)
В(а)
Отрицания: А(х)→В(х), В(а)
А(а)
Силлогизма: А(х) → В(х), В(х) → С(х)
А(х) → С(х)
Слайд 29
Структура доказательства
Пример:
Сумма смежных углов равна 180°.
тезис
аргументы
демонстрация
Слайд 31
Понятия «рассуждение» и «доказательство»
Рассуждение – это цепочка суждений,
каждое из которых логически вытекает из предыдущего (предыдущих)
А В С …
Слайд 32
Понятия «рассуждение» и «доказательство»
Рассуждение – это цепочка суждений,
каждое из которых логически вытекает из предыдущего (предыдущих)
А В С …
Доказательство – это рассуждение, в котором каждый шаг аргументирован
?! ?! ?! ?!
А В С … Z
Слайд 33
Рассуждаем или доказываем?
Верно ли, что значение выражения
а ∙ 15 – 10 делится нацело на 5?
Слайд 34
Виды рассуждений
Необходимо различать рассуждения трёх видов:
содержательное рассуждение (неаргументированное
рассуждение в силу недостаточности знаний);
аргументированное рассуждение (доказательство);
свёрнутое рассуждение (неаргументированное
рассуждение, которое при необходимости может быть дополнено учеником до рассуждения второго вида).
Слайд 35
Развитие умения рассуждать
содержательное рассуждение
аргументированное рассуждение (доказательство);
свёрнутое рассуждение
Слайд 36
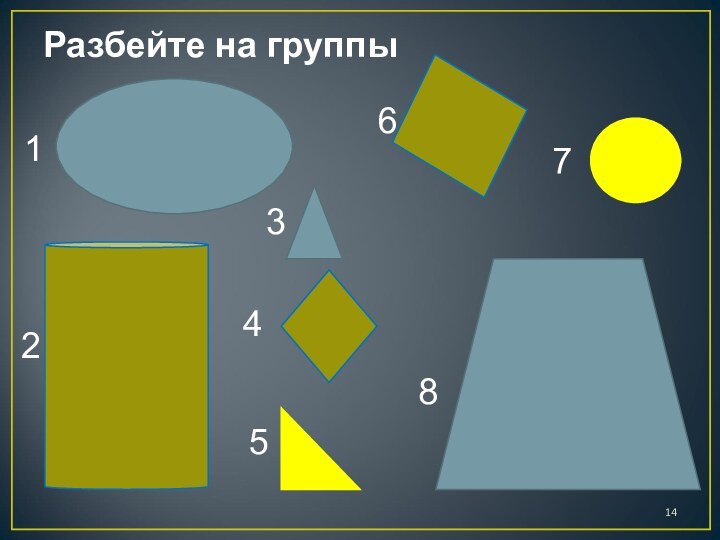
Соотнесите
виды рассуждений
с этапами
обучения доказательству
Слайд 37
Литература
Лакатос И. Доказательство и опровержение. М.: Наука, 1967.
Пиаже
Ж. Избранные психологические труды. М., 1994.
Пиаже Ж. Эволюция интеллекта
в подростковом и юношеском возрасте // Психологическая наука и образование. 1997. № 4. С. 56-64.
Подгорецкая Н.А. Изучение приемов логического мышления у взрослых. М.: Изд-во Моск. гос. ун-та, 1980. 150 с.
Столяр А.А. Педагогика математики. Учеб. пособие для студентов физ.-мат. факультетов педагогических вузов. Минск: Вышэйшая школа , 1986. 414 с.
Слайд 38
Методика обучения предмету
Зачем?
Чему?
Как?
Слайд 39
Методические подходы к обучению доказательству
Использование программного материала
с четким указанием способа и уровня
обоснованности (строгое или нестрогое рассуждение), приведением образцов полных (аргументированных) рассуждений и т. п.
Использование содержания, методов и средств, не предусмотренных программой.
Слайд 40
Различные подходы к обучению логическим рассуждениям
Работа с предложениями,
содержащими кванторы.
раскрытие содержания суждений со словами “все”, “некоторые” и
т. п.;
образование предметной интерпретации, соответствующей данному суждению;
самостоятельное описание заданной ситуации с использованием общих, частных и единичных суждений;
распознавание одинаковых по содержанию общих и частных суждений;
уточнение формулировок утверждений с целью выделения их вида.
Е. П. Маланюк
Слайд 41
Различные подходы к обучению логическим рассуждениям
Связь дедуктивных и
индуктивных рассуждений.
образцы рассуждений,
разнообразные задания, в которых отрабатывается порядок предложений
в умозаключении.
Например:
Ответь, правильно ли данное рассуждение (умозаключение). Если нет, то почему?”
Продолжи рассуждение.
Детям предлагаются два листа, на одном из которых написаны общие посылки, на другом – частные посылки. Учащиеся устанавливают, какой общей посылке соответствует каждая частная.
В. П. Лёхова
Слайд 42
Различные подходы к обучению логическим рассуждениям
Опора на логические
операции анализа и сравнения.
Может ли неизвестное число в уравнении
х – (27 + 4) = 4 равняться 27?
На сколько уменьшаемое больше вычитаемого, если х – 80 = 200?
Укажите среди данных те уравнения, которые нельзя решить:
28 – х = 30
35 + х = 70
15 + х = 12.
Н. Б. Истомина
Слайд 43
Различные подходы к обучению логическим рассуждениям
Знакомство обучающихся с
логическими правилами вывода (Г.И. Саранцев, Г.Р. Бреслер, Б.Д. Пайсон
и др.)
Заключения: А(х)→В(х), А(а)
В(а)
Отрицания: А(х)→В(х), В(а)
А(а)
Силлогизма: А(х) → В(х), В(х) → С(х)
А(х) → С(х)
Слайд 44
Различные подходы к обучению логическим рассуждениям
Работа с понятиями.
Задачи
на исследование.
Логические задачи.
Магические квадраты.
Текстовые задачи (решение арифметическим методом).
…
Слайд 45
Задание
Составьте задание для обучающихся начальной школы, направленное
на развитие умения рассуждать, используя при этом программный материал
(можно опираться на названные выше приемы/подходы)
Слайд 46
Построение локальных теорий
Теория – это “совокупность обобщённых положений,
образующих науку или раздел какой-нибудь науки”.
Слово “локальный” означает “местный,
не выходящий за определённые пределы”.
(Ожегов С.И. Словарь русского языка. М., 1988. С. 648. С. 266)
Термин “локальная теория” будем понимать как совокупность обобщённых положений, относящихся к конкретной теме
Слайд 47
Построение математической теории как один из трёх основных
аспектов математической деятельности:
математическое описание конкретных ситуаций, или математизация эмпирического
материала (МЭМ);
логическая организация математического материала (ЛОММ), полученного в результате первого аспекта деятельности, или построение математической теории (“маленькой, локальной”, или “большой, глобальной”);
применение математической теории (ПМТ), полученной в результате второго аспекта деятельности
Слайд 50
Ученик достигает понимания математики, если в процессе обучения
он принимает активное участие в развитии математических идей, процедур,
в построении (пусть и маленьких, локальных) математи-ческих теорий
А.А. Столяр
Слайд 51
Примеры локальных теорий
Игра «Кирпичики»
ЛТ «Четные и нечетные числа»
ЛТ
«Углы»
ЛТ «Параллельные прямые»
ЛТ «Ромб» и др.