Слайд 2
Условие:
Задача С3.
Два игрока играют
в следующую игру. На координатной плоскости стоит фишка. Игроки
ходят по очереди. В начале игры фишка находится в точке с координатами (5,2). Ход состоит в том, что игрок перемещает фишку из точки с координатами (x,y) в одну из трех точек: или в точку с координатами (x+3,y), или в точку с координатами (x,y+3) или в точку с координатами (x,y+4). Выигрывает игрок, после хода которого расстояние по прямой от фишки до точки с координатами (0,0) не меньше 13 единиц. Кто выигрывает при безошибочной игре обоих игроков – игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте
Решение:
Слайд 3
Критерии оценки:
Указания по оцениванию:
пункт 1 - 3 балла - Правильное указание выигрывающего
игрока и его ходов со строгим доказательством правильности (с помощью или без помощи дерева игры)
Слайд 4
Критерии оценки:
пункт 2:
2
балла - правильное указание выигрывающего игрока, стратегии игры, приводящей
к победе, но при отсутствии доказательства ее правильности.
Слайд 5
Критерии оценки:
пункт 3:
1 балл - При
наличии в представленном решении одного из пунктов:
часть 1. Правильно
указан выигрывающий игрок, и его первый ход, рассмотрены все возможные ответы второго игрока, но неверно определены дальнейшие действия
часть 2. Правильно указан выигрывающий игрок и его первый ход, но описание выигрышной стратегии неполно и рассмотрены несколько (больше одного, но не все) вариантов ответов второго игрока.
Слайд 6
Критерии оценки:
пункт 4
0 баллов - Задание
не выполнено или в представленном решении полностью отсутсвует описание
элементов выигрышной стратегии, и отсутствует анализ вариантов первого - второго ходов играющих (даже при наличии правильного указания выигрывающего игрока)
Слайд 7
Табличный способ решения:
Этот способ наиболее трудоёмкий,
но самый надёжный.
Нам предстоит построить, а затем и
заполнить не совсем простую таблицу, ее еще называют - "дерево игры" .
Проведём предварительный анализ и ответим на два вопроса:
1.Сколько строк и столбцов будет в таблице?
Слайд 8
Определим количество столбцов
Для того, чтобы определить количество столбцов
воспользуемся подсказкой☺
В критериях оценки этого задания есть следующий пункт:
ставиться ноль баллов, если отсутствует анализ первого и второго ходов играющих. Т.к. играющих два, то столбцов – четыре.
Слайд 9
Определим количество строк:
1. Первый игрок имеет право на
три различных хода (из условия), значит ему отведём –
три строки.
2.Второй может ответить на каждый ход первого так же тремя ходами. Итого: 3*3 =9 строк (вариантов)
3. Первый может ответить тремя вариантами на каждый из девяти ходов второго. 9*3 =27 строк
4. Сколько ответных ходов может сделать второй игрок? Правильно : 81
Слайд 10
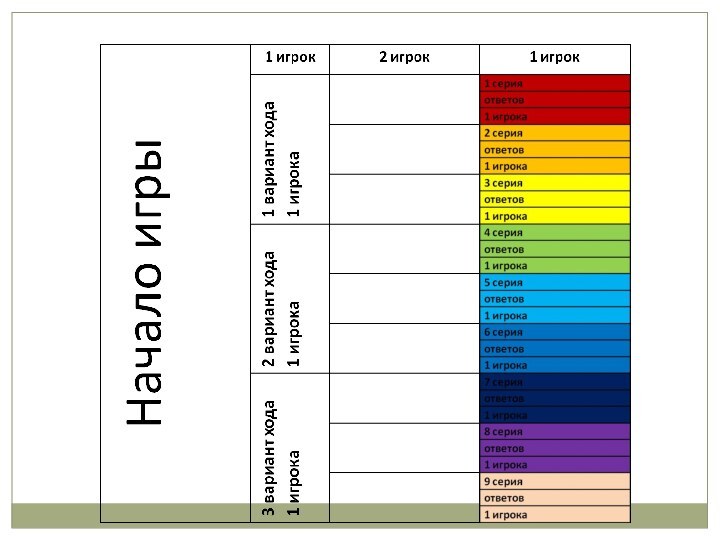
Построение таблицы
Такую большую таблицу рисовать необязательно.
Можно «схитрить».
Итак, лучше
начать рисовать таблицу справа налево. Для этого очерчиваем прямоугольник
в 27 строк. Затем слева к нему пристраиваем столбец, объединяя каждые три строки предыдущего столбца в один. Снова отступ влево и повторяем предыдущую процедуру.
Почему же не 81 строка?
Слайд 11
Вот так!)))
Вся хитрость в том, что
на каждую серию ответов первого игрока нам достаточно будет
указать один выигрышный ход.
Слайд 13
Как будем определять победителя?
Из рисунка видно,
что нам нужно определить длину вектора S, которая зависит
от изменения координат фишки игроком. Как найти длину вектора S?
Длину вектора S можно рассчитать по теореме Пифагора:
Слайд 14
Вспомним условие:
По условию задачи выигрывает тот,
кто первым удалится от начала координат на 13 или
больше единиц.
Предположим первый игрок перешел в точку с координатами (8;2), проверим этот ход на победу с помощью теоремы Пифагора
Значит до победы первому игроку далеко.
Слайд 15
Важно!
Чтобы не запутаться при заполнении таблицы,
необходимо соблюдать следующие правила:
Первый ход всегда по оси X
Второй
ход по оси Y на минимальное удаление
Третий ход по оси Y на максимальное удаление
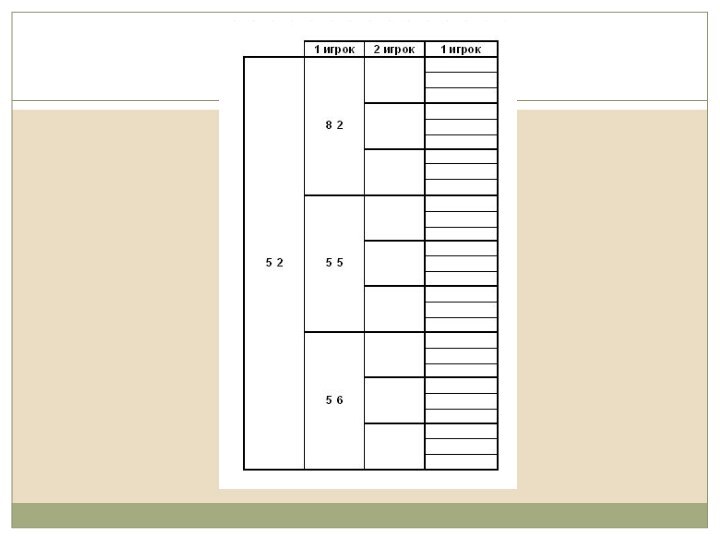
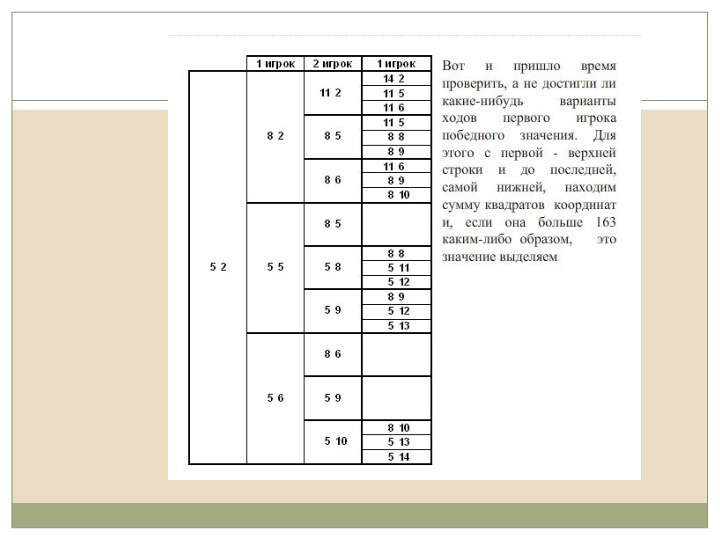
Можно приступить к заполнению таблицы. В первый столбец поставим начальную координаты фишки (5;2). В верхнюю строку первого хода первого игрока, согласно условию, внесем координаты (8;2).
Слайд 16
Заполнение таблиц
Выполните таблицу, о которой говорилось
ранее, у себя в тетради и заполните всевозможные первые
ходы первого игрока.
Слайд 23
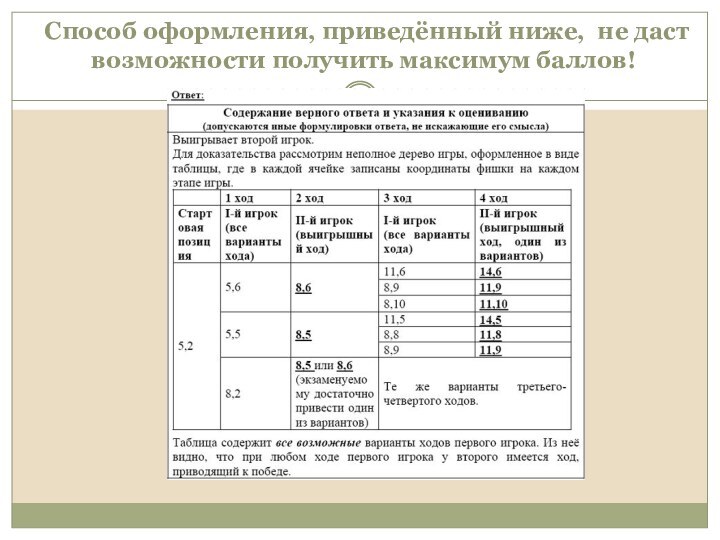
Способ оформления, приведённый ниже, не даст возможности
получить максимум баллов!
Слайд 24
Вернемся к критериям оценки:
Вспомним пункт 3, часть 1
где говорится:...если правильно указан выигрывающий игрок и его первый
ход, но описание выигрышной стратегии неполно и рассмотрены несколько (больше одного, но не все) вариантов ответов второго игрока - 1 балл.
Слайд 25
Вернемся к критериям оценки:
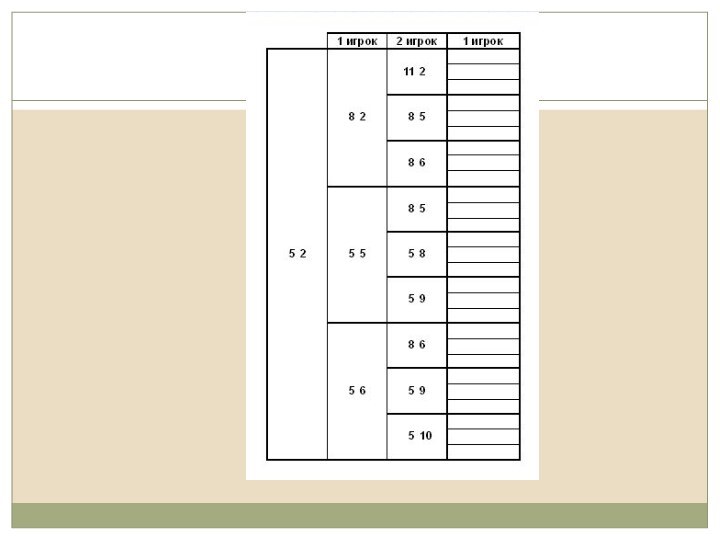
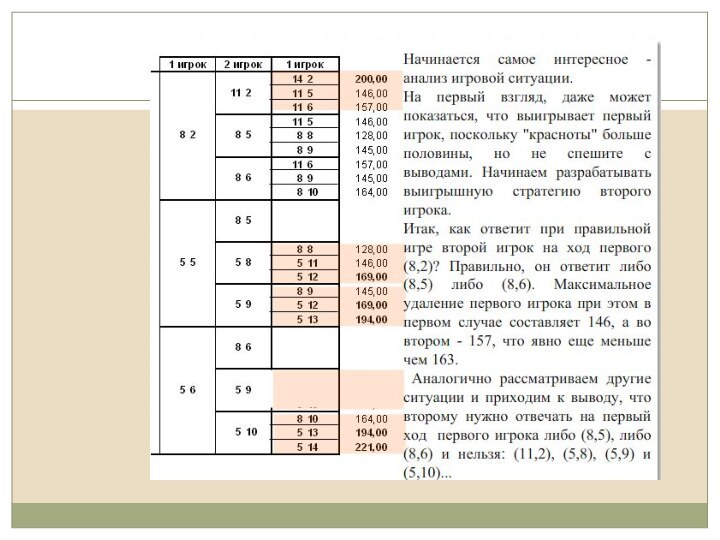
Невооруженным глазом видно, что второй
игрок после хода первого может поставить фишку в точки
с координатами: (11,2), (8,5), (8,6), (5,8), (5,9),(5,10) из которых в таблице рассмотрены только (8,5) и (8,6), т.е. по такому оформлению невозможно строго доказать, к чему приводит ход (5,10) - к победе либо наоборот к поражению, если его не рассматривать?
Слайд 26
Вернемся к критериям оценки:
не успокаивайте себя,
что 1 балл - тоже хорошо, поскольку пунк 4
гласит: ...если отсутствует анализ вариантов первого - второго ходов играющих (даже при наличии правильного указания выигрывающего игрока) - 0 баллов, а теперь скажите, сколько возможных вариантов хода есть у второго игрока, после того как сходит первый - девять, а в ответе рассмотрено сколько - 4. О чем это говорит? Это говорит о том, что отсутствует анализ целых пяти вариантов из возможных. Следовательно, если вы даже укажете, что победит второй вам могут поставить за него 0 баллов!!!
Слайд 27
Вернемся к критериям оценки:
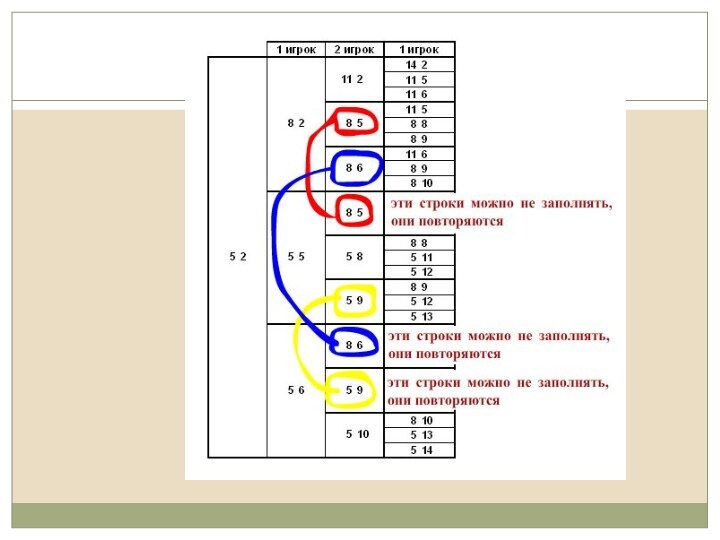
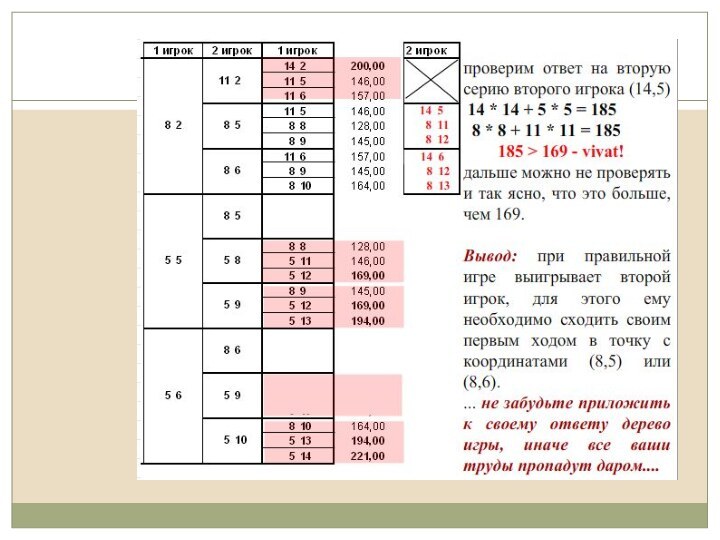
Иными словами, приведенная выше таблица
содержит все возможные варианты только первого хода и только
первого игрока, но не рассматривает и половину из тех, которые может сделать второй на первом ходу, а про второй ход обоих игроков даже и говорить не приходится…
Слайд 28
Ещё один пример задачи С3
Задача « Камушки».
Два игрока
играют в игру. Перед ними лежат две кучки камней,
в первой из которых 3, а во второй – 2 камня. У каждого игрока неограниченное число камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то кучке, или добавляет 1 камень в какую-то кучку. Выигрывает игрок, после хода которого общее число камней в двух кучках становится не менее 16. Кто выигрывает при правильной игре – игрок, делающий первый ход, или игрок делающий второй ход. Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.
Слайд 29
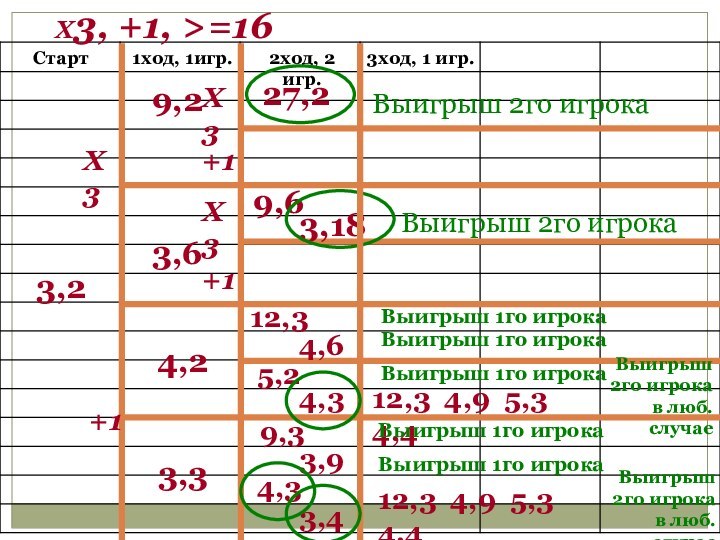
Х3, +1, >=16
Старт
3,2
Х3
+1
9,2
3,6
4,2
3,3
1ход, 1игр.
2ход, 2 игр.
Х3
+1
27,2
Выигрыш 2го игрока
Х3
+1
9,6
3,18
Выигрыш
2го игрока
12,3
4,6
5,2
4,3
9,3
3,9
4,3
3,4
3ход, 1 игр.
Выигрыш 1го игрока
Выигрыш 1го игрока
Выигрыш 1го
игрока
12,3 4,9 5,3 4,4
Выигрыш 2го игрока в люб.случае
Выигрыш 1го игрока
Выигрыш 1го игрока
12,3 4,9 5,3 4,4
Выигрыш 2го игрока в люб.случае