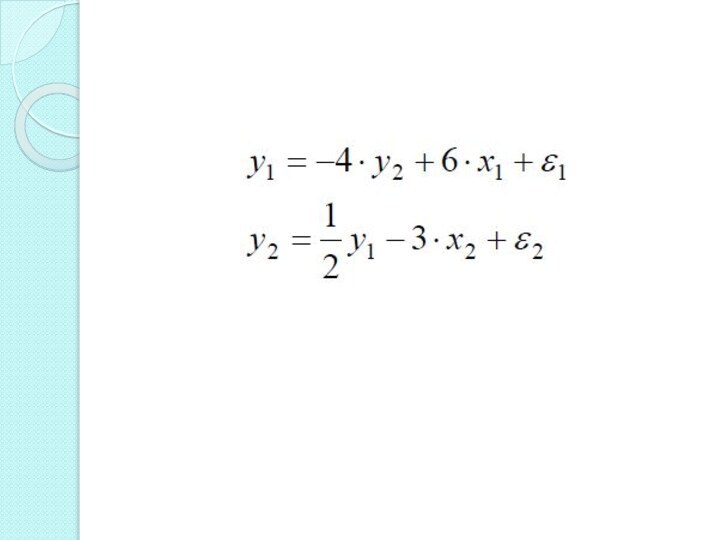Слайд 2
4.1. Структурная и приведенная формы модели
В случае сложных
экономических систем изменение какого-либо признака повлечет за собой изменения
во всей системе взаимосвязанных признаков.
Эконометрические модели строятся в виде систем эконометрических уравнений.
Слайд 3
Модель равновесной цены
где Pt – средняя цена за
единицу товара, Qt- объем предложения товара, It- средний уровень
дохода, t-текущий период времени, a10, a20, a11, b11, b21 – постоянные параметры, ε1t, ε2t – ошибки уравнений.
Слайд 4
Макроэкономическая модель Клейна
Слайд 5
Переменные в системах эконометрических уравнений подразделяются на эндогенные
и экзогенные.
Эндогенными переменными называются взаимозависимые переменные, которые определяются внутри
модели (системы). (y, равно числу уравнений системы).
Экзогенными (предопределенные) переменными называются переменные, которые определяются вне системы. (обозначаемые буквой x).
К предопределенным переменным относятся и лаговые (значения переменных за предыдущие моменты времени) переменные системы.
Слайд 6
CNt, It, W1t, Yt, Рt, Кt, Wt, Et
– эндогенные переменные;
Gt, W2t, ТХt и (YEAR – 1931)
– экзогенные переменные;
Кt-1, Р t-1 и E t-1 – лаговые переменные.
Слайд 7
Система эконометрических уравнений с n зависимыми переменными yi
Слайд 9
функции предопределенных переменных хi
Слайд 14
4.2. Оценка параметров структурной формы модели
Структурная и приведенная
формы модели содержат разное число параметров п·(п–1) + n·т
и n·т.
Чтобы уравнять число параметров, необходимо предположить равенство нулю некоторых структурных коэффициентов модели либо наличие между ними определенных соотношений, например, а11 + b12 = 0.
Слайд 15
вида структурных моделей
– идентифицируемые системы;
–неидентифицируемые системы;
– сверхидентифицируемые системы.
Слайд 16
Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо,
и неидентифицируемой, если хотя бы одно из уравнений системы
неидентифицируемо. Сверхидентифицируемая модель содержит только идентифицируемые и сверхидентифицируемые уравнения.
Слайд 17
Необходимое условие идентифицируемости.
H число эндогенных переменных в уравнении,
а через D – число предопределенных переменных, отсутствующих в
уравнении, но присутствующих в системе.
Необходимое условие идентифицируемости формулируется следующим образом:
– уравнение идентифицируемо, если D+1 = H;
– уравнение неидентифицируемо, если D+1 < H;
– уравнение сверхидентифицируемо, если D+1> Н.
Слайд 18
Достаточное условие идентифицируемости.
Уравнение, соответствующее переменной yi, идентифицируемо, если
ранг матрицы, составленной из коэффициентов при переменных модели, отсутствующих
в исследуемом уравнении, но входящих в остальные уравнения системы, равен числу эндогенных переменных системы без единицы:
rang([B A]i )=n-1,
где [BA] – блочная матрица коэффициентов, составленная из матриц B и A;
[BA]i– матрица, полученная из матрицы [BA] в результате удаления i-строки и столбцов, соответствующих объясняющим переменным входящим в i-уравнение.
Слайд 19
Проверим достаточное условие для первого уравнения системы конъюнктурной
модели.
Эндогенные переменные модели: Сt,It,rt,Yt.
Предопределенные переменные модели: Мt,Gt,Ct–1,It–1.
Общая матрица [BA]
коэффициентов уравнений системы, столбцы которой соответствуют переменным Сt, It, rt, Yt, Мt, Gt, Ct–1, It–1 имеет вид
Слайд 21
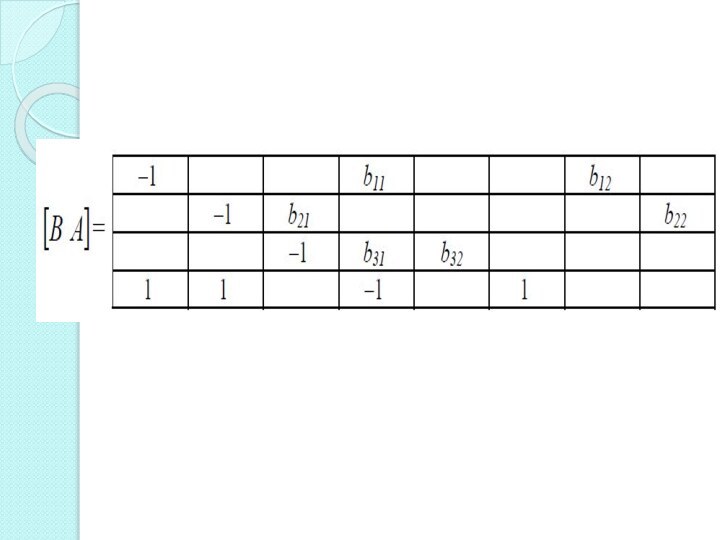
Первое уравнение содержит переменные Сt, Yt, Ct–1. Запишем
матрицу
[BA]1, полученную вычеркиванием из матрицы [B A] первой строки
и столбцов, соответствующих переменным Сt, Yt, Ct–1
Слайд 22
4.3. Косвенный метод наименьших квадратов
Косвенный МНК используется в
случае идентифицируемой системы уравнений и заключается в следующем:
1) исходная
система уравнений преобразуется в приведенную форму модели и определяются численные значения параметров δij для каждого ее уравнения в отдельности с помощью традиционного МНК;
Слайд 23
2) путем алгебраических преобразований осуществляется переход от приведенной
формы к уравнениям структурной формы модели, что автоматически дает
численные оценки структурных параметров.
Слайд 24
ПРИМЕР
Требуется найти структурные параметры модели
при условии, что полученная
приведенная форма модели описывается уравнениями
Слайд 25
Проверим идентифицируемость уравнений. В модели имеется две эндогенные
переменные у1, у2 и две экзогенные переменные x1, x2.
В
первое уравнение входят две эндогенные переменные у1,у2 и одна экзогенная переменная x2.
Следовательно, H = 2, D = 1 и H = D + 1, и первое уравнение – идентифицируемо. Идентифицируемость второго уравнения доказывается аналогично.
Слайд 26
Для нахождения структурных коэффициентов можно применить косвенный МНК,
т.е. получить их с помощью преобразования приведенных уравнений.
Слайд 28
4.4. Двухшаговый метод наименьших квадратов
Численные значения структурных параметров
определяются в следующей последовательности:
1) Исходная система уравнений преобразуется в
приведенную форму модели и определяются численные значения параметров δij для каждого ее уравнения в отдельности с помощью традиционного МНК;
Слайд 29
2) По полученным уравнениям приведенной формы находятся расчетные
значения
инструментальных переменных y*i, соответствующих эндогенным переменным уi для каждого
наблюдения;
3) С помощью обычного МНК определяются параметры каждого структурного уравнения в отдельности, используя в качестве факторов фактические
значения предопределенных переменных и полученные расчетные значения инструментальных переменных y*i.
Слайд 30
Модифицированную модель Кейнса
где Y – валовой национальный доход;
С
– личное потребление;
I – инвестиции;
G – государственные расходы;
t и
t–1 обозначают текущий и предыдущий периоды;
ε1 и ε2 – случайные ошибки.
Слайд 32
В модели имеются три эндогенные переменные Yt, Сt,
It и две предопределенные переменные Yt-1 и Gt.
Первое уравнение
сверхидентифицируемо, т. к. H = 2, D = 2 и H < D + 1.
Второе уравнение идентифицируемо,
т. к. H = 2, D = 1 и H = D + 1.
Слайд 33
Применяя МНК последовательно к уравнениям структурной формы модели
получим
окончательный вид структурной формы модели












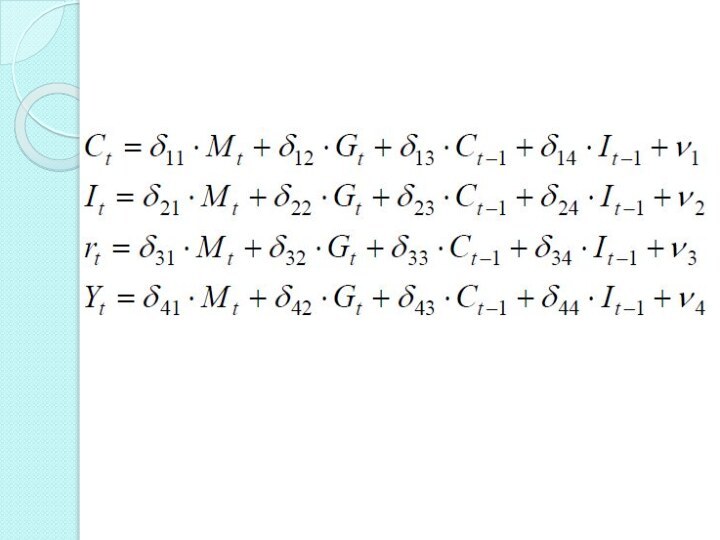






![4. Системы эконометрических уравнений Первое уравнение содержит переменные Сt, Yt, Ct–1. Запишем матрицу[BA]1, полученную вычеркиванием из](/img/tmb/14/1361251/8228089e73edbc55b077fa1643c33260-720x.jpg)