Презентация на тему по теме Перестановки 7 класс

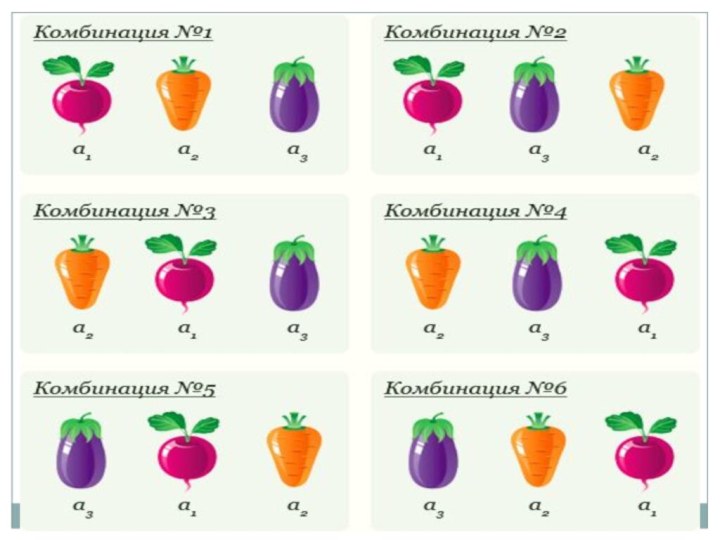
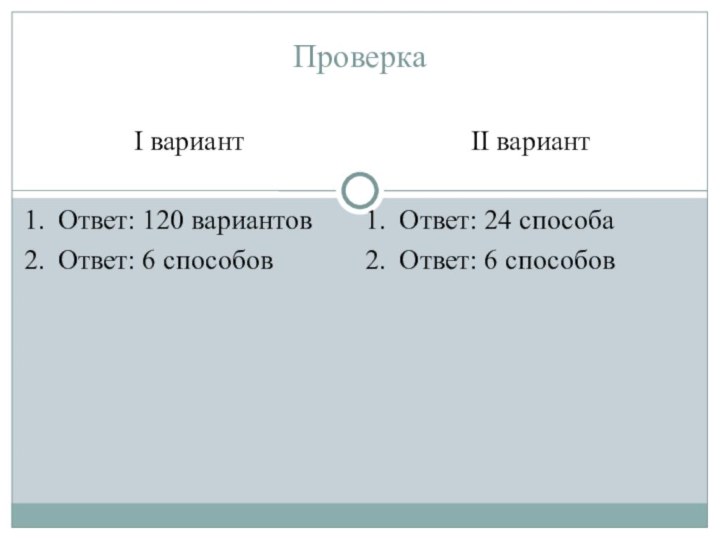
перестановок
3. Познакомиться с понятием «факториал»
4. Научиться применять формулу перестановок

вывод формулы
3. Решение задач на применение формулы перестановок
4.

из основателей
теории вероятностей и
математического анализа Якоб Бернулли

состоящие из одних и тех же n различных элементов и отличающиеся

сыграть Квартет

идущих первых n натуральных чисел обозначают n! и читают

= 1∙2 = 2
3! = 1∙2∙3 = 6
Запомни

3! = 3∙2∙1
Р4 = 4! = 1∙2∙4∙5
Р5 = 5!

в) 6!;
г)7!





Ответы:
а) 24
б) 120
в) 720
г) 5040

горизонтально три одинаковых по величине куска материи белого, синего

Решение.
Р3 = 3! = 1∙2∙3 = 6
Ответ: 6 способов

Флаг Югославии

4! + 2!;
б) 3!∙2!;
в)5! :

Ответы:
а) 26;
б) 12;
в) 5

= 8!∙ 9, то 9!∙6! = 8!∙ 9

учебного дня из 5 различных уроков?
2. Аня, Вера и

IIвариант
1.   Сколькими способами можно расставить 4 различные книги на книжной полке?
2. Сколькими способами могут стать в очередь в билетную кассу 3 человека?

способа
Ответ: 6 способов

строка – два прилагательных, выражающих главную мысль.
3 строка –

№611, №612,
II уровень: №616, №621.