- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по теории вероятностей и математической статистике для СПО
Содержание
- 2. История Задачи о кёнигсбергских мостахИздавна среди жителей
- 3. Река (Преголя)Прего́ля (прусск. Preigara, Preigile, нем. Pregel)
- 4. Можно ли…?В 1736 году задача о семи мостах заинтересовала
- 5. Кто такой Леонард Эйлер?Леона́рд Э́йлер (нем. Leonhard
- 6. Решение вопроса, связанного с геометрией положенияСтатья Эйлера
- 7. Результаты рассужденийВ ходе рассуждений Эйлер пришёл к
- 8. ВыводГраф кёнигсбергских мостов имел четыре (синим) нечётные
- 9. Применение теории графовСозданная Эйлером теория графов нашла очень широкое
- 10. Дальнейшая история мостов КёнигсбергаВ 1905 году был
- 11. Скачать презентацию
- 12. Похожие презентации
История Задачи о кёнигсбергских мостахИздавна среди жителей Кёнигсберга была распространена такая загадка: как пройти по всем мостам (через реку Преголя), не проходя ни по одному из них дважды. Многие кёнигсбержцы пытались решить эту задачу как теоретически,










Слайд 3
Река (Преголя)
Прего́ля (прусск. Preigara, Preigile, нем. Pregel) —
река, впадающая в Балтийское море, точнее в Калининградский (Вислинский)
залив. Длина Преголи — 123 км, вместе с Анграпой (один из важнейших притоков) — 292 км. Площадь бассейна Преголи — 15,5 тыс. км².
Слайд 4
Можно ли…?
В 1736 году задача о семи мостах заинтересовала выдающегося
математика, члена Петербургской академии наук Леонарда Эйлера, о чём
он написал в письме итальянскому математику и инженеру Мариони от 13 марта 1736 года. В этом письме Эйлер пишет о том, что он смог найти правило, пользуясь которым, легко определить, можно ли пройти по всем мостам, не проходя дважды ни по одному из них. Ответ был «нельзя».
Слайд 5
Кто такой Леонард Эйлер?
Леона́рд Э́йлер (нем. Leonhard Euler;
15 апреля 1707, Базель, Швейцария — 7 (18) сентября
1783, Санкт-Петербург, Российская империя) — швейцарский, немецкий и российский математик и механик, внёсший фундаментальный вклад в развитие этих наук (а также физики, астрономии и ряда прикладных наук).
Слайд 6
Решение вопроса, связанного с геометрией положения
Статья Эйлера 1736
года «Решение вопроса, связанного с геометрией положения» положила начало теории графов
как математической дисциплине. Поводом для исследования послужила задача о семи мостах Кёнигсберга: можно ли пройти каждый мост по одному разу и вернуться в исходное место?Эйлер формализовал её, сведя к задаче о существовании в графе (вершины которого отвечают частям города, разделённым протоками реки Преголя, а рёбра — мостам) циклического маршрута, проходящего по каждому ребру ровно один раз (в современной терминологии — эйлерова цикла).
Решая последнюю задачу, Эйлер показал: для наличия эйлерова цикла в графе нужно, чтобы у каждой вершины её степень (число выходящих из вершины рёбер) была чётной (а в задаче о кёнигсбергских мостах это не так: степени равны 3, 3, 3 и 5).
Слайд 7
Результаты рассуждений
В ходе рассуждений Эйлер пришёл к следующим
выводам:
Число нечётных вершин (вершин, к которым ведёт нечётное число
рёбер) графа должно быть чётно. Не может существовать граф, который имел бы нечётное число нечётных вершин.Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.
Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.
Слайд 8
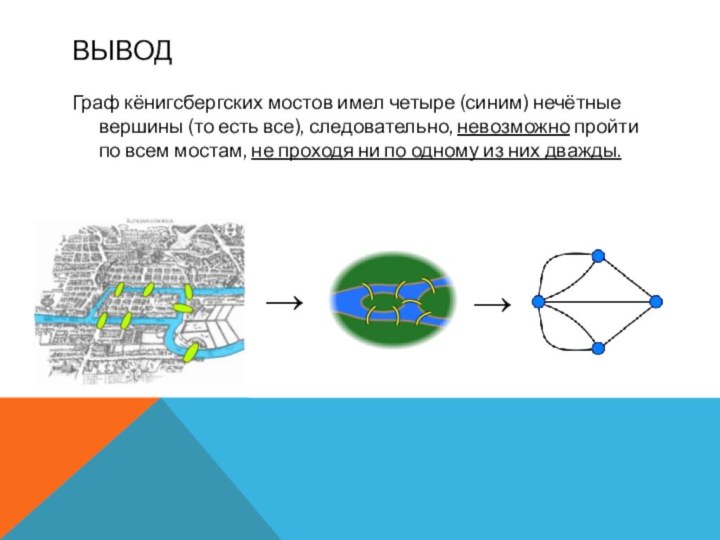
Вывод
Граф кёнигсбергских мостов имел четыре (синим) нечётные вершины
(то есть все), следовательно, невозможно пройти по всем мостам,
не проходя ни по одному из них дважды.→
→
Слайд 9
Применение теории графов
Созданная Эйлером теория графов нашла очень широкое применение
в транспортных и коммуникационных системах (например, для изучения самих
систем, составления оптимальных маршрутов доставки грузов или маршрутизации данных в Интернете).
Слайд 10
Дальнейшая история мостов Кёнигсберга
В 1905 году был построен
Императорский мост, который был впоследствии разрушен в ходе бомбардировки
во время Второй мировой войны.Существует легенда о том, что этот мост был построен по приказу самого кайзера, который не смог решить задачу мостов Кёнигсберга и стал жертвой шутки, которую сыграли с ним учёные умы, присутствовавшие на светском приёме (если добавить восьмой мост, то задача становится разрешимой).
На опорах Императорского моста в 2005 году был построен Юбилейный мост. На данный момент (2015 год) в Калининграде восемь мостов.





























