иные возможные значения, наперед неизвестные и зависящие от случайных
причин, которые заранее не могут быть учтены.Обозначение СВ: X, Y, Z и т.д.
или Xi
Обозначение значений СВ: х, y, z, …
или xi
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть















Обозначение СВ: X, Y, Z и т.д.
или Xi
Обозначение значений СВ: х, y, z, …
или xi
На практике встречаются два основных типа случайных величин:
1. Дискретные случайные величины (ДСВ);
2. Непрерывные случайные величины (НСВ).
Случайной величиной называется числовая функция от случайных событий.
Дискретными случайными величинами называются случайные величины, принимающие только отдаленные друг от друга значения, которые можно заранее перечислить.
xn
x2
x1
x3 …
p1
p2
p3
pn
.
.
.
.
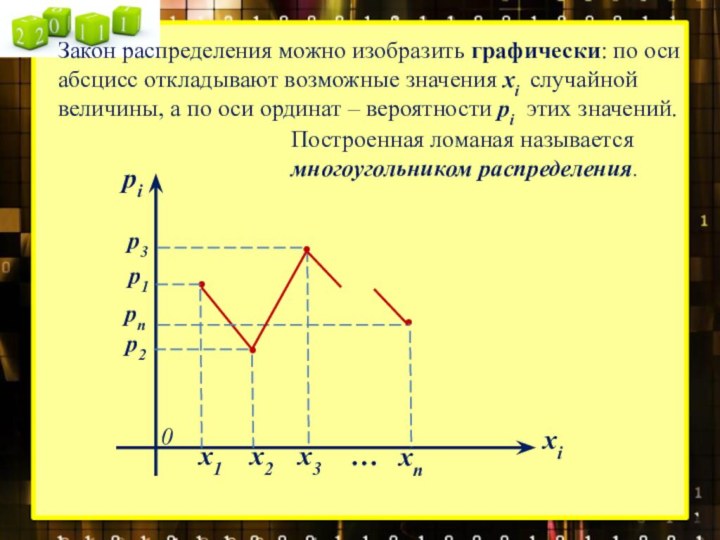
Построенная ломаная называется
многоугольником распределения.
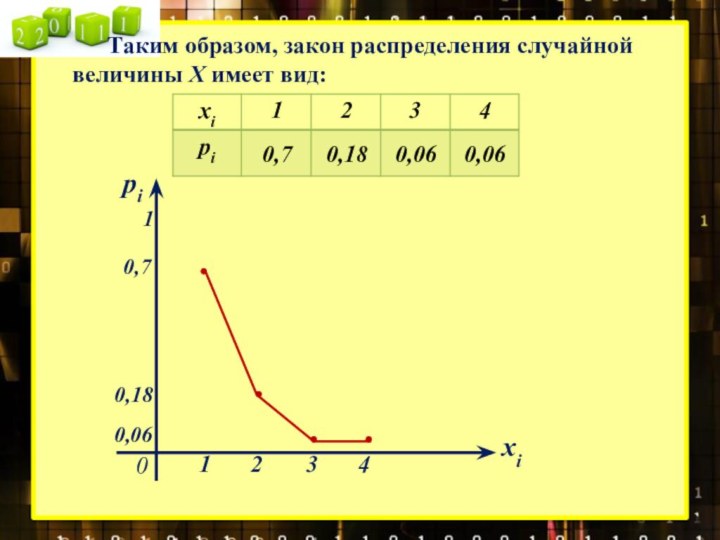
Решение. Случайная величина X – число патронов, израсходованных охотником, может принимать значения 1, 2, 3, 4.
p1 = P(X = 1) = p(A1) = 0,7 - охотник попал в цель с первого выстрела;
Решение. Случайная величина X – число станков, которые в течение часа потребуют регулировки,может принимать значения
0,1, 2, 3.
- в течение часа какие-либо 2 станка потребуют регулировку;
- в течение часа только 1 станок потребует регулировки;
- в течение часа все три станка потребуют регулировку;
Проверка: p1 + p2 + p3 + p4 =
0,504+0,398+0,092+0,006=1 - верно
Решение. Случайная величина X – числа покупателей, совершивших покупку, может принимать значения 0, 1, 2, 3, 4.
p1 = P(X = 4) =
p2 = P(X = 3) =
p3 = P(X = 2) =
p4 = P(X = 1) =
p5 = P(X = 0) =
все 4 совершили покупки
3 покупателей совершили покупки
2 покупателей совершили покупки
1 покупатель совершил покупки
0 покупателей совершили покупки
Еськова Ирина Павловна, БУ «Междуреченский агропромышленный колледж», 2019 г.