Успешного усвоения нового материала
Основная мысль урокаОкружающий нас мир – это мир геометрии.
А.Д. Александров
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть









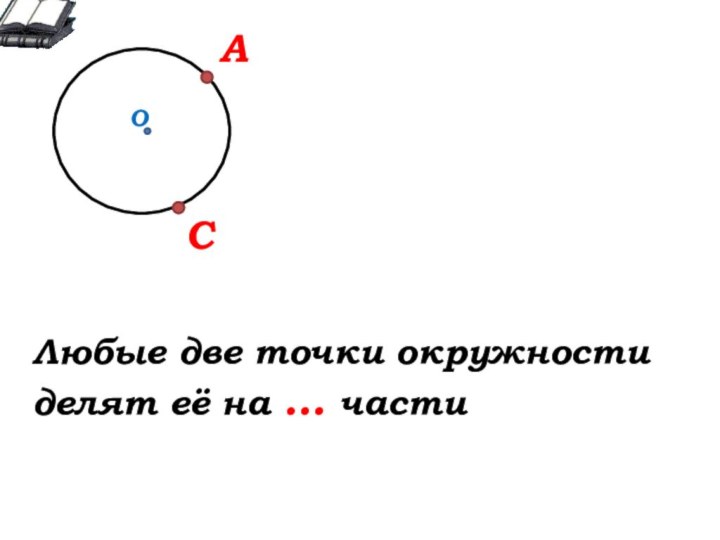
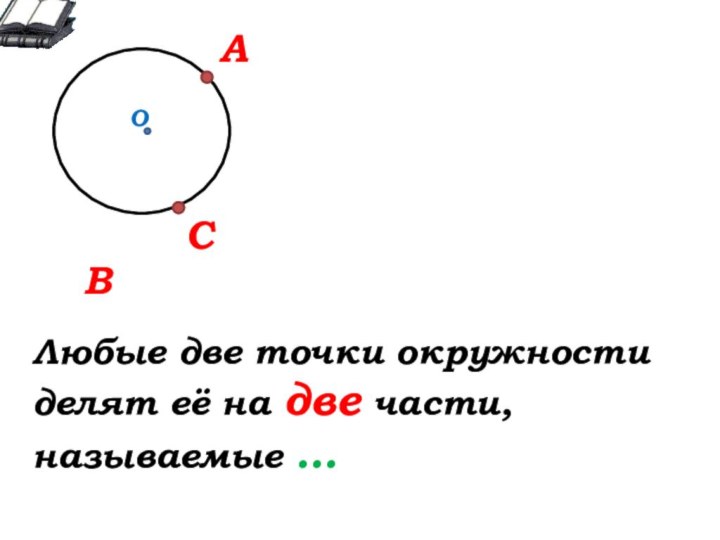
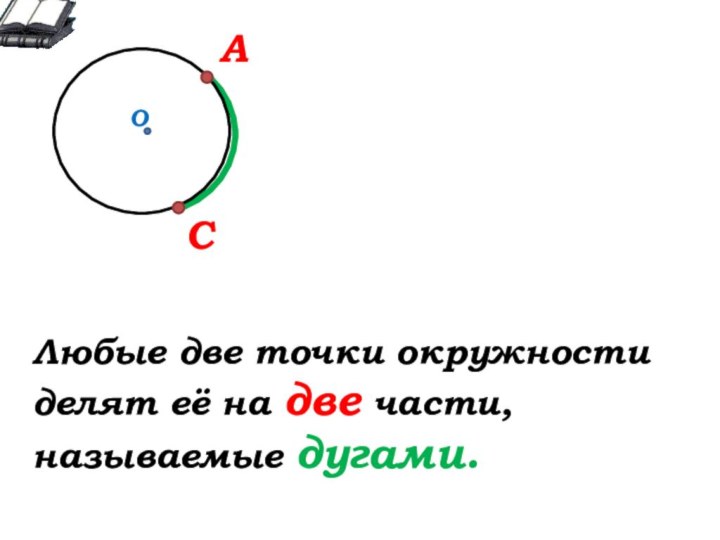
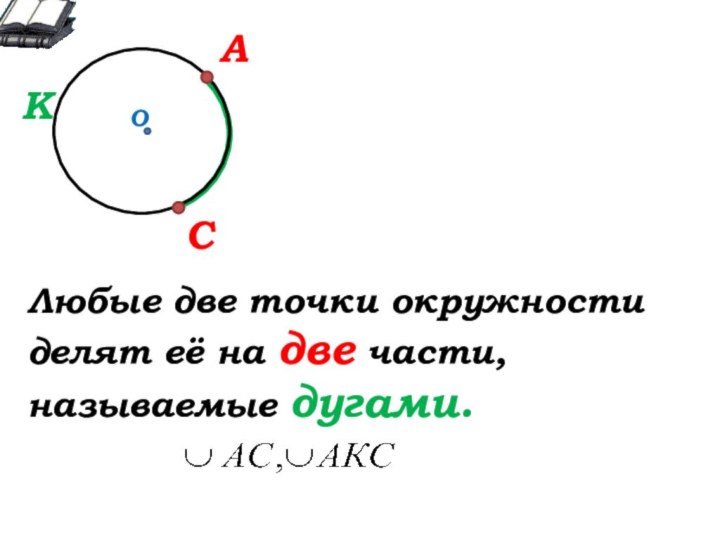
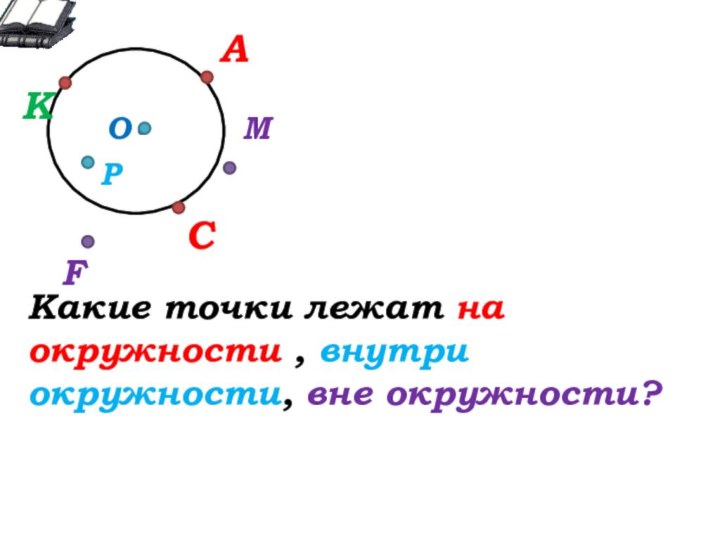
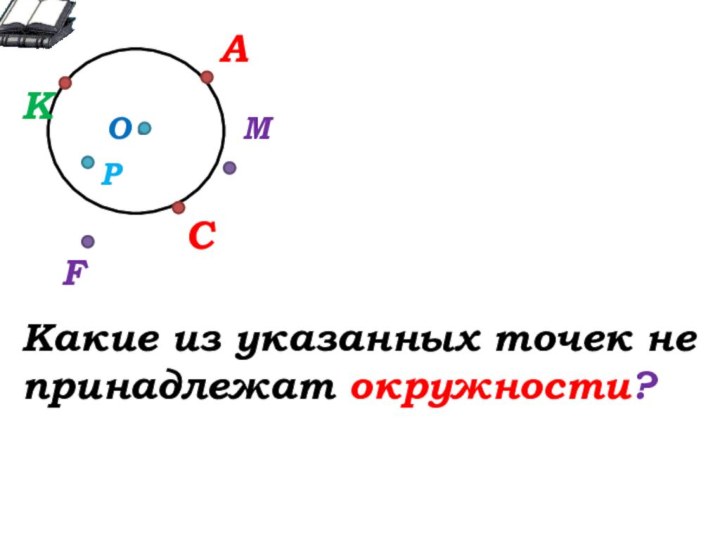






Окружающий нас мир – это мир геометрии.
А.Д. Александров
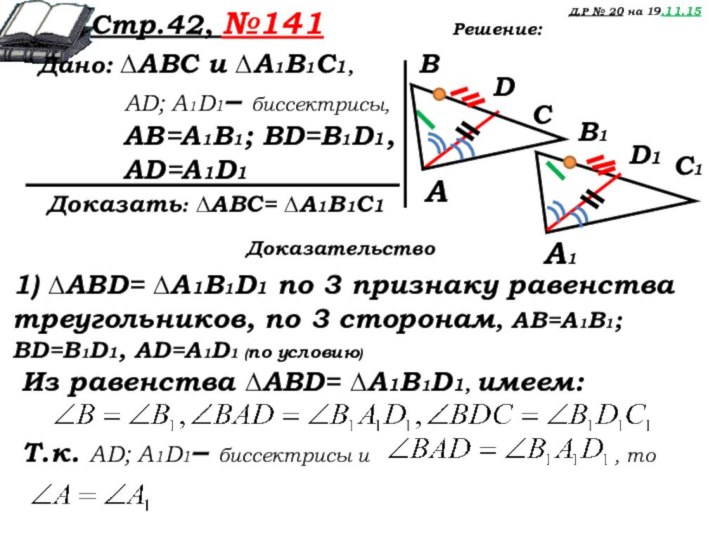
Решение:
1) ∆АВD= ∆А1В1D1 по 3 признаку равенства треугольников, по 3 сторонам, AВ=А1В1; ВD=B1D1, AD=A1D1 (по условию)
Из равенства ∆АВD= ∆А1В1D1, имеем:
Т.к. AD; A1D1– биссектрисы и , то
Доказательство
А
В
С
А1
В1
С1
D1
D
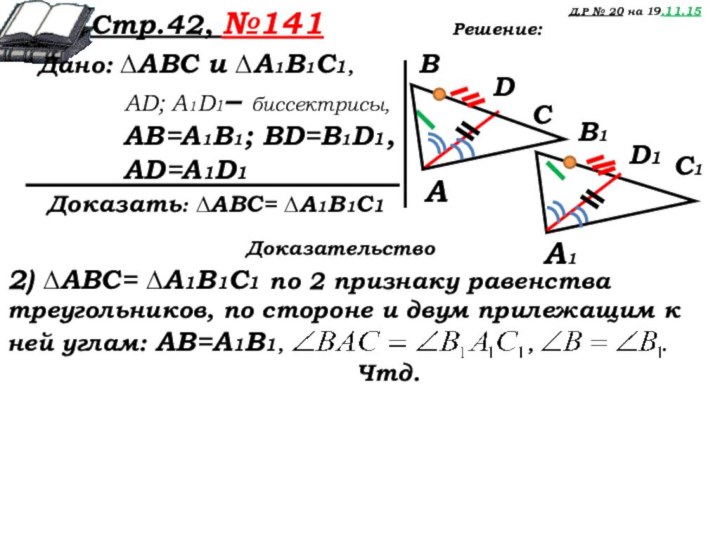
Решение:
2) ∆АВC= ∆А1В1C1 по 2 признаку равенства треугольников, по стороне и двум прилежащим к ней углам: AВ=A1В1, , .
Чтд.
Доказательство
А
В
С
А1
В1
С1
D1
D
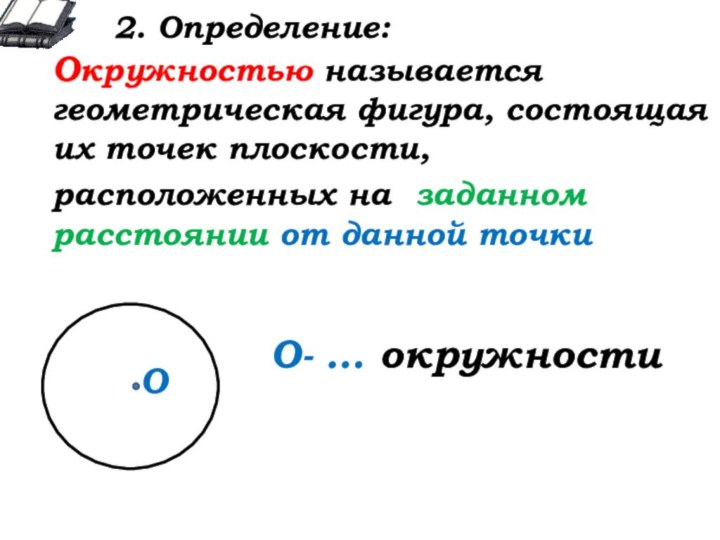
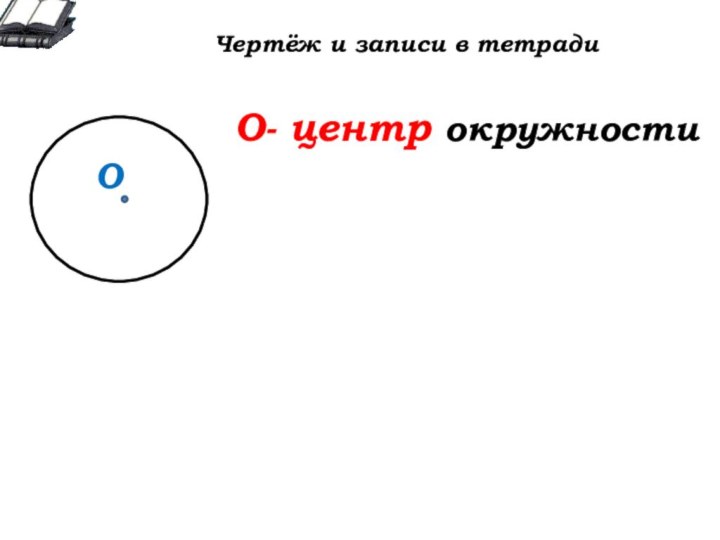
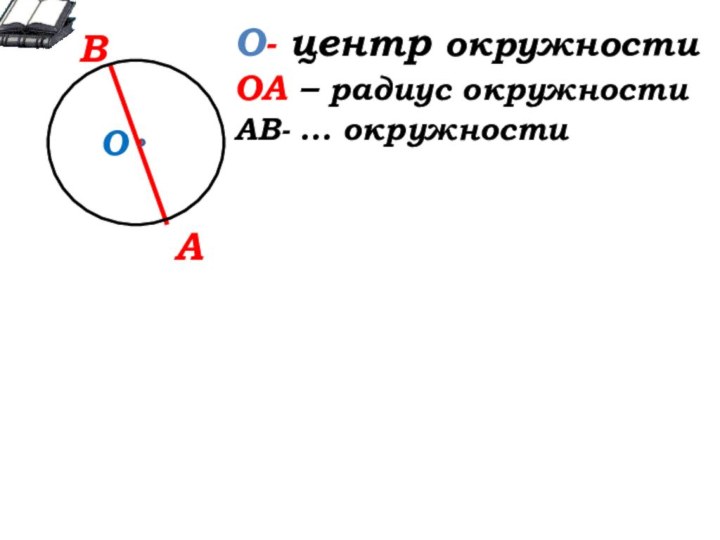
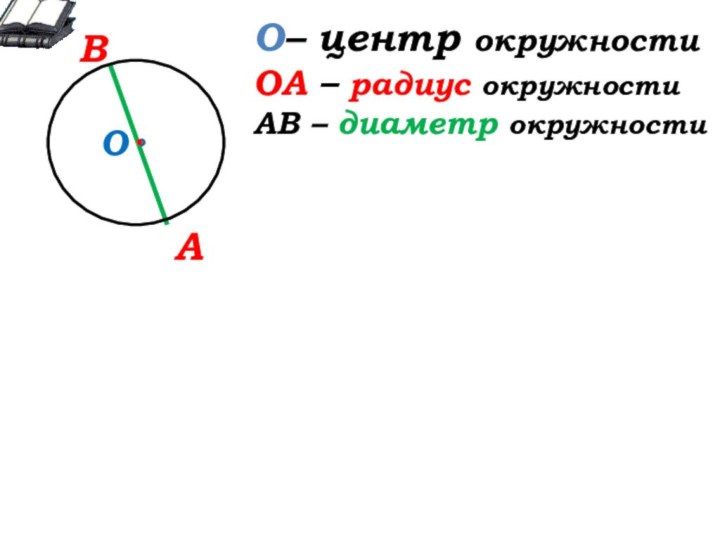
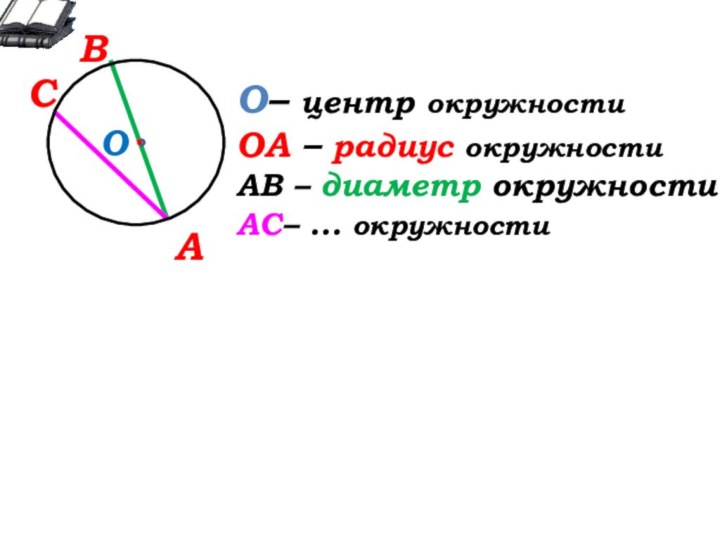
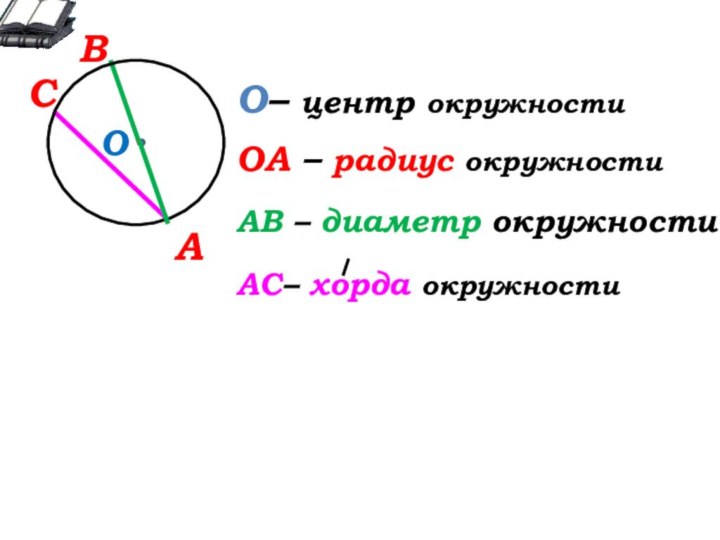
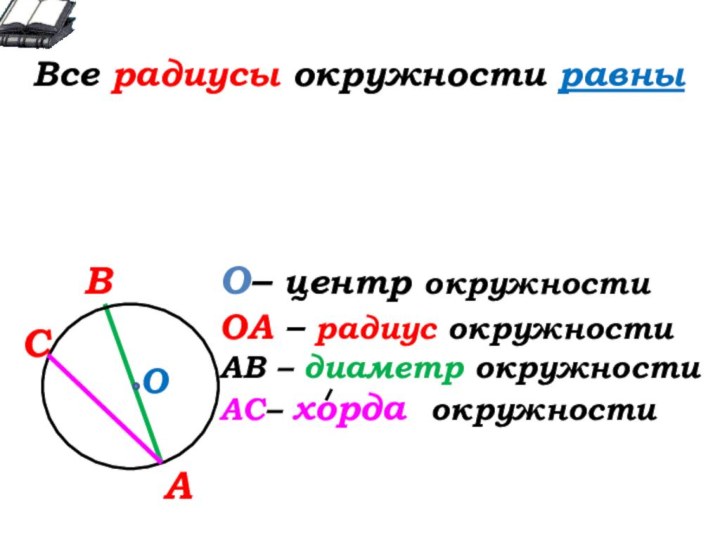
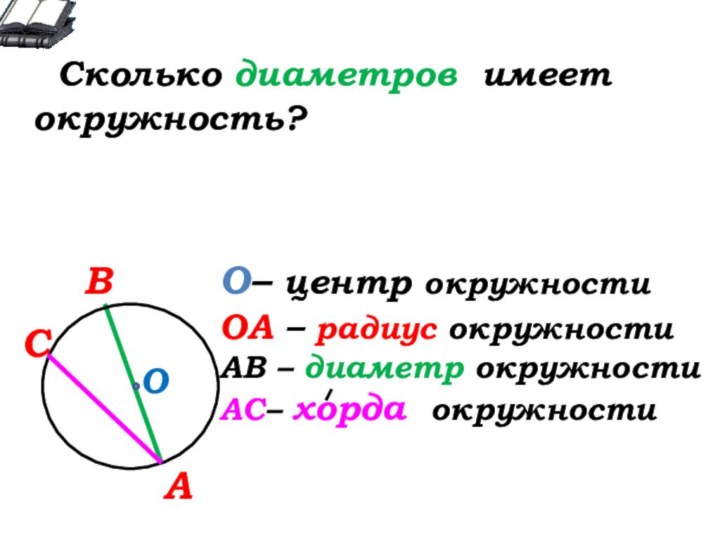
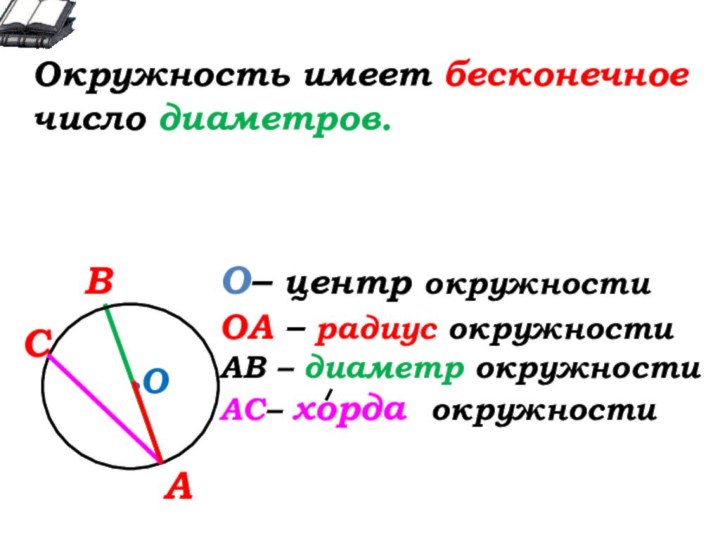
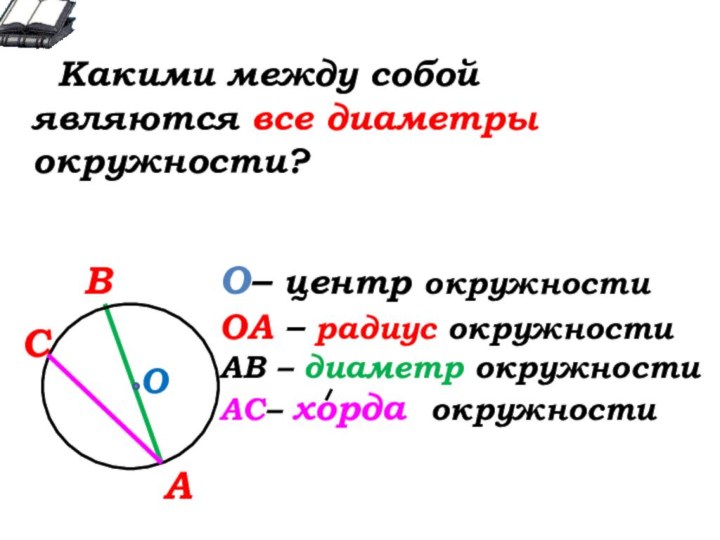
О
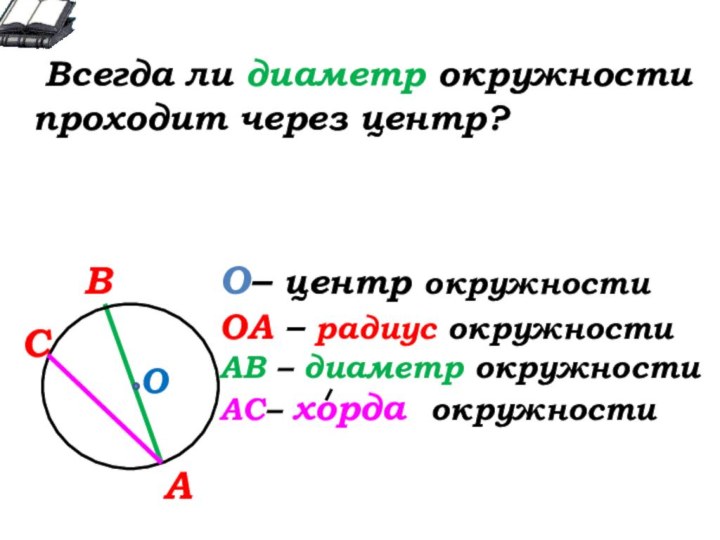
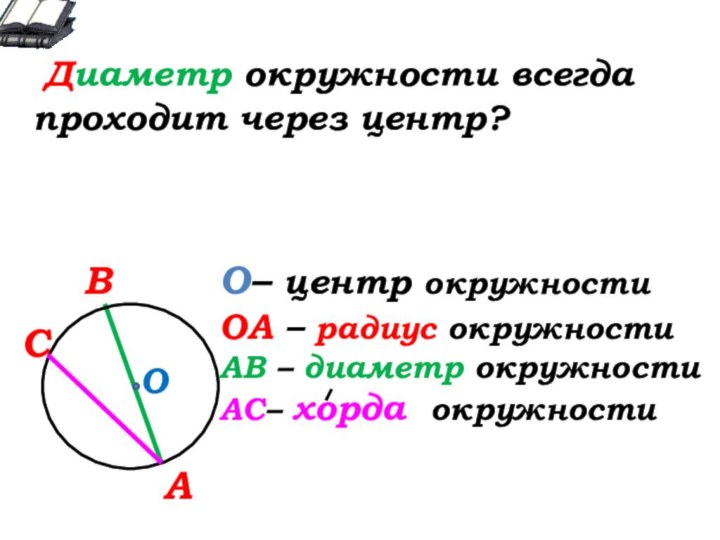
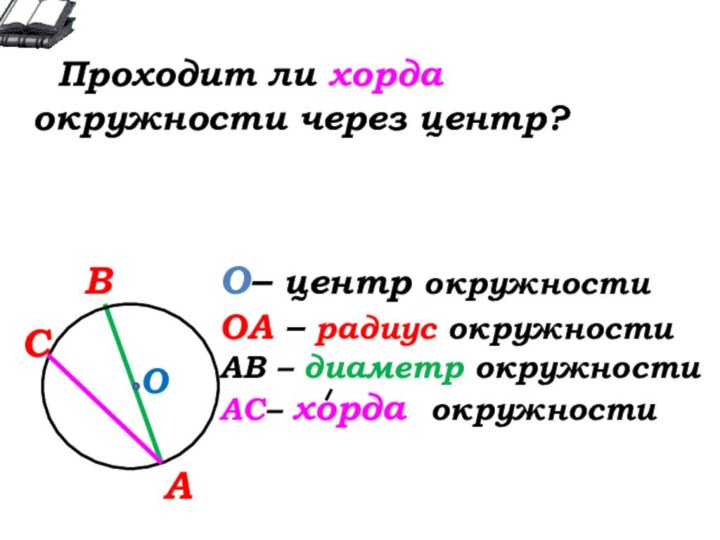
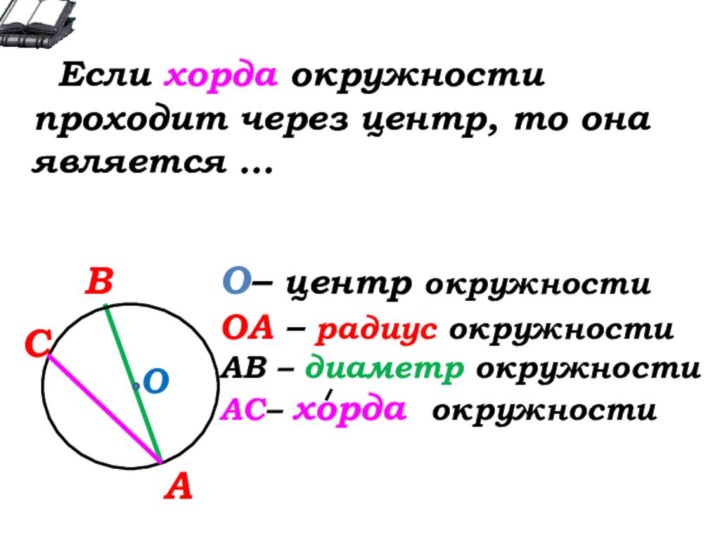
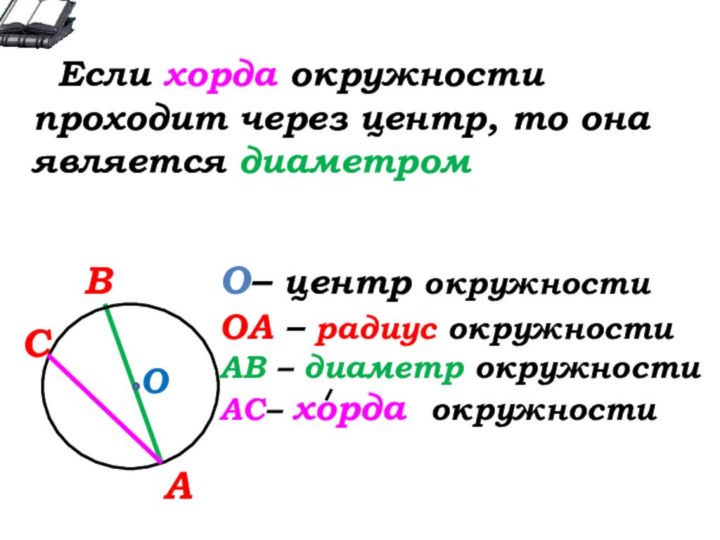
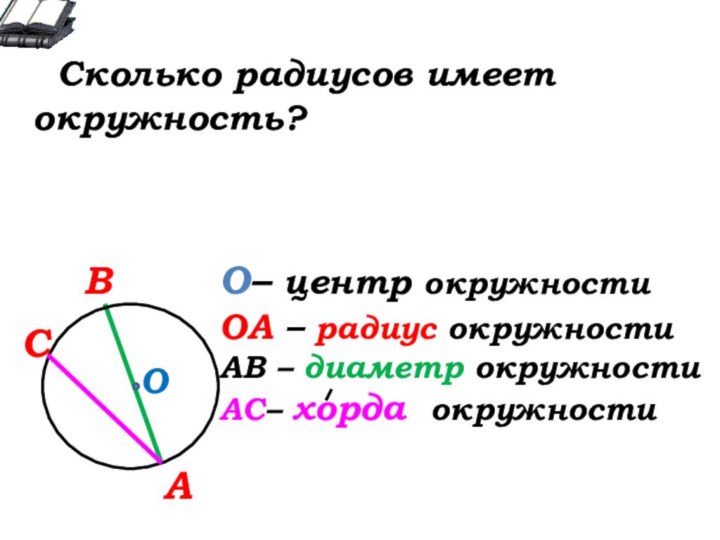
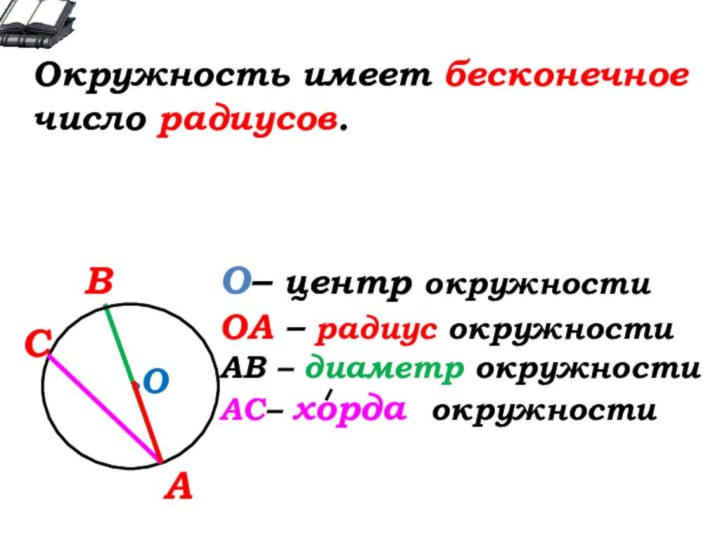
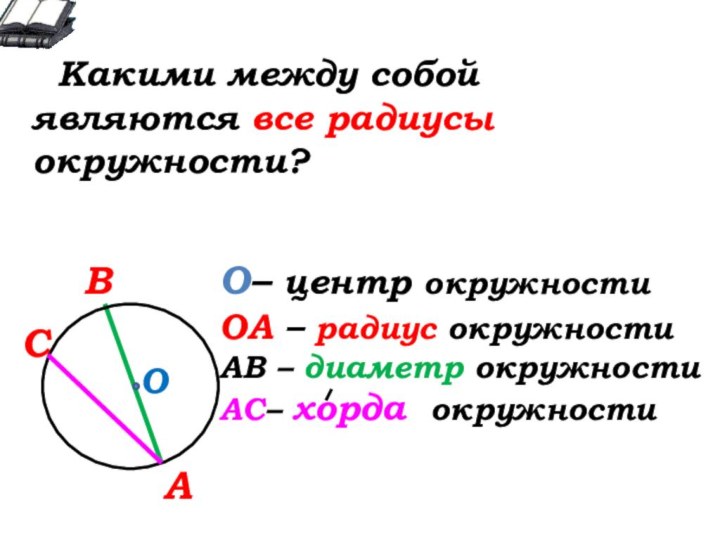
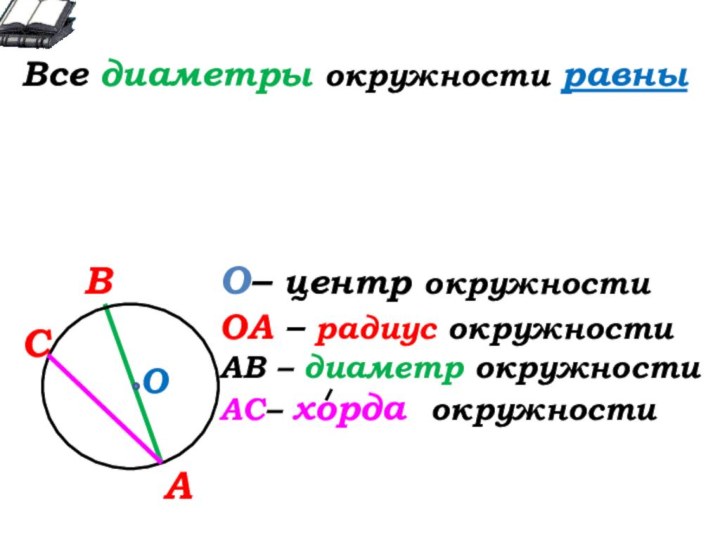
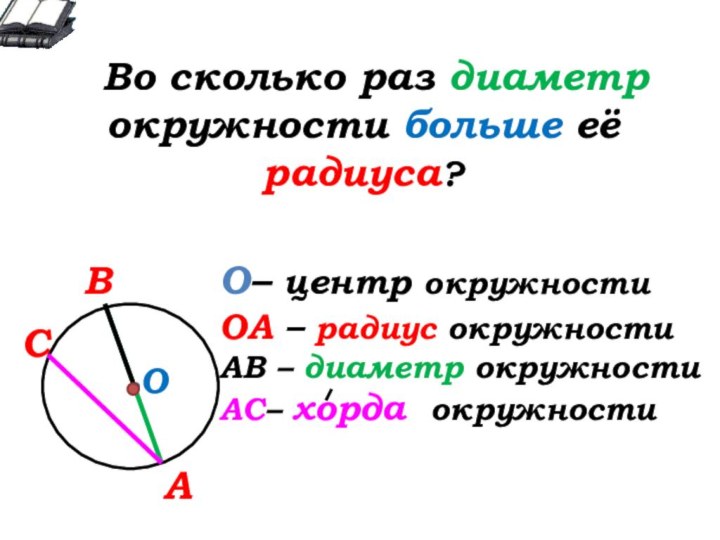
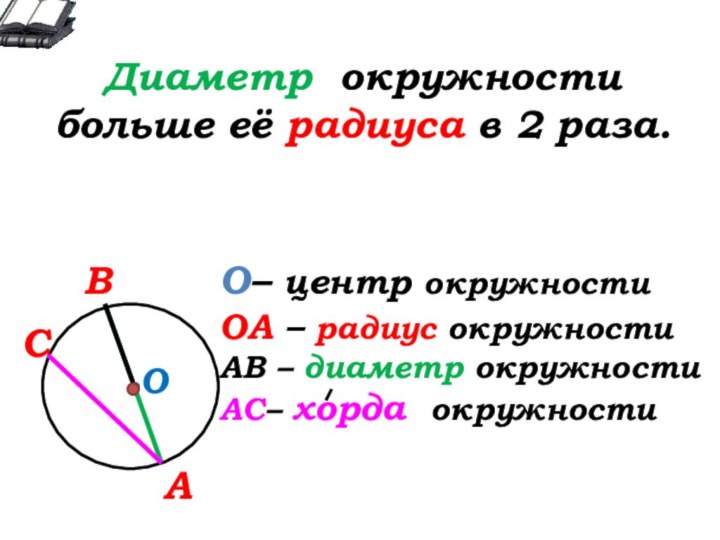
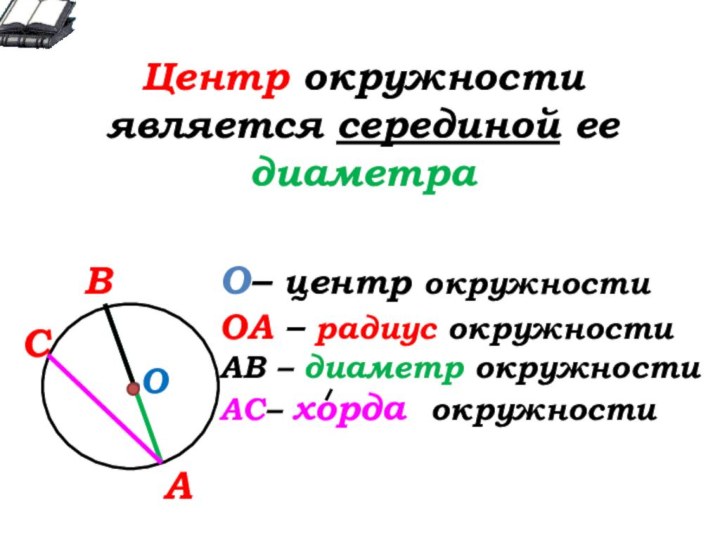
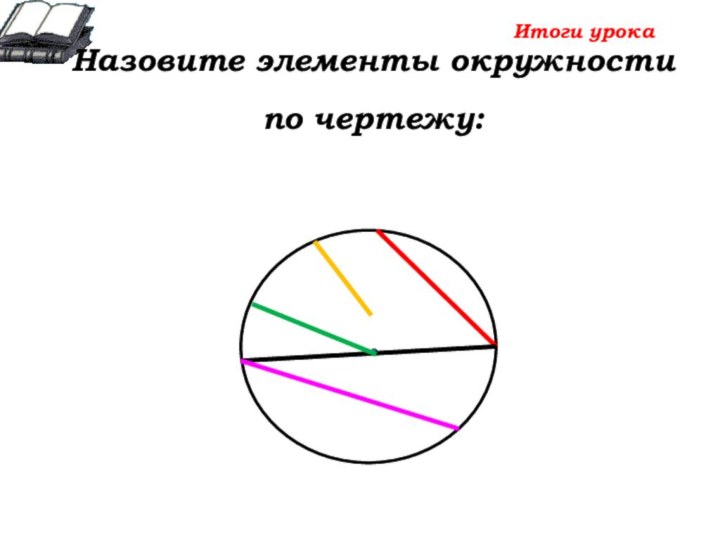
О- … окружности
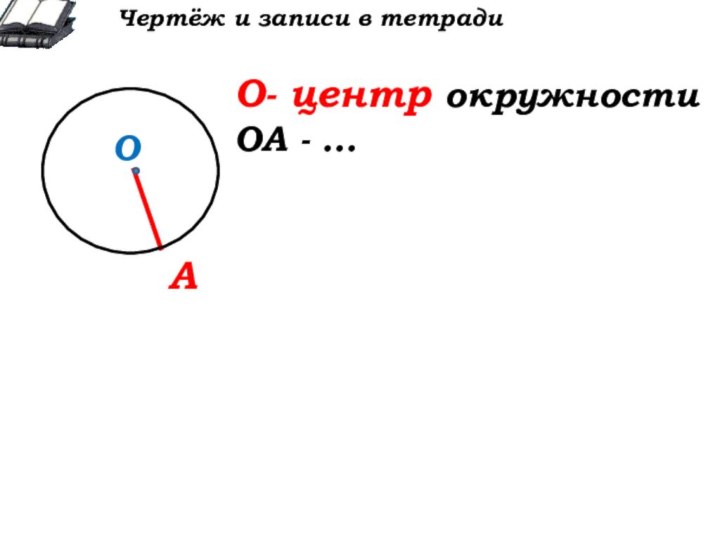
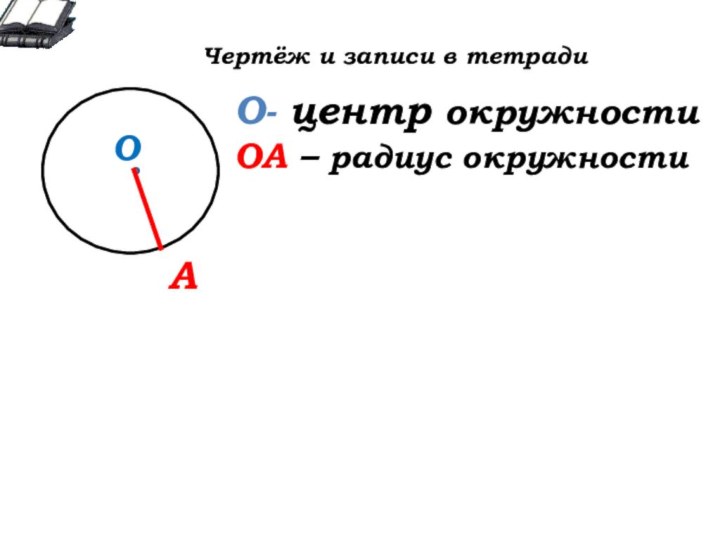
А
В
С
А
В
С
А
В
С
А
В
С
А
В
С
А
В
С
А
В
С
А
В
С
А
В
С
А
В
С
А
В
С
А
В
С
А
В
С
А
В
С
А
В
С
А
В
С
А
В
С
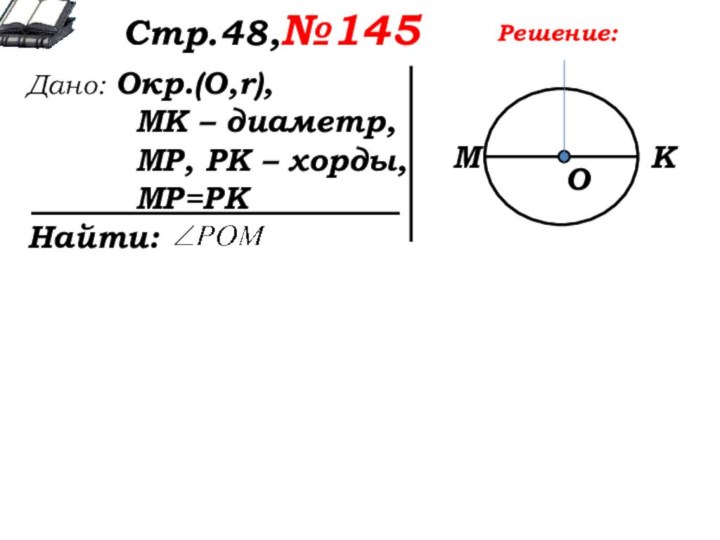
М
К
Р
О
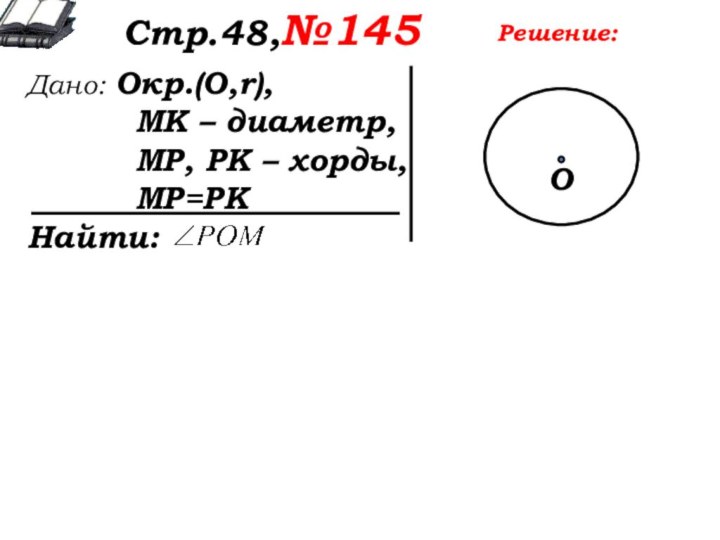
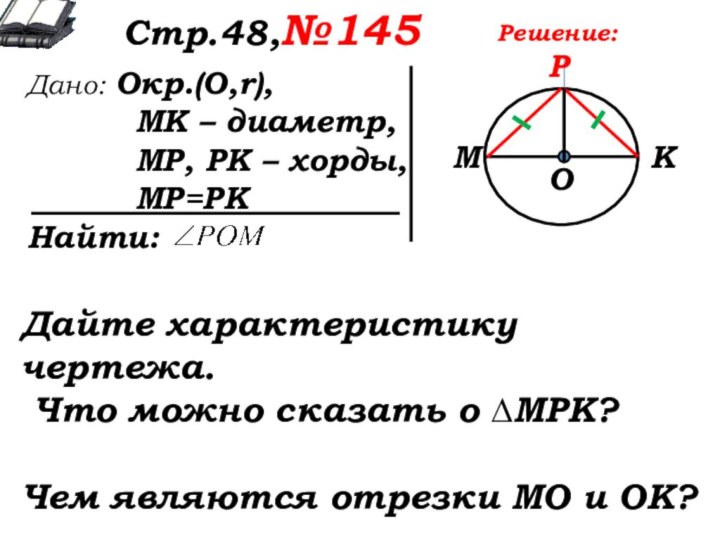
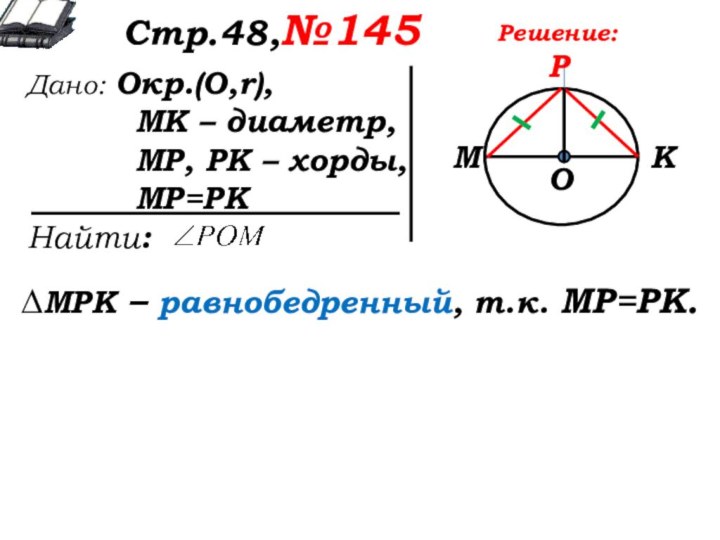
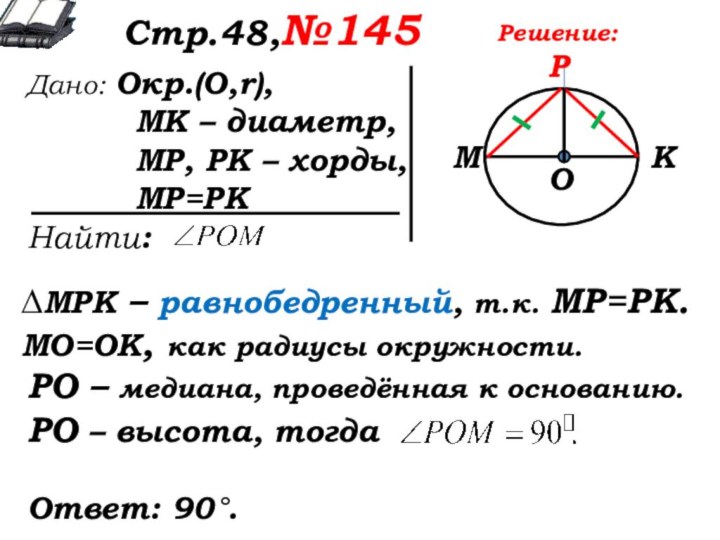
Решение:
Дайте характеристику чертежа.
Что можно сказать о ∆МРК?
Чем являются отрезки МО и ОК?
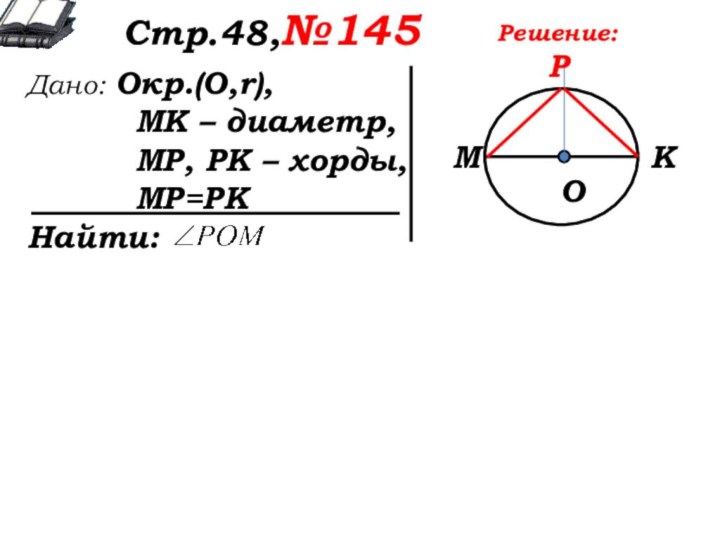
М
К
Р
О
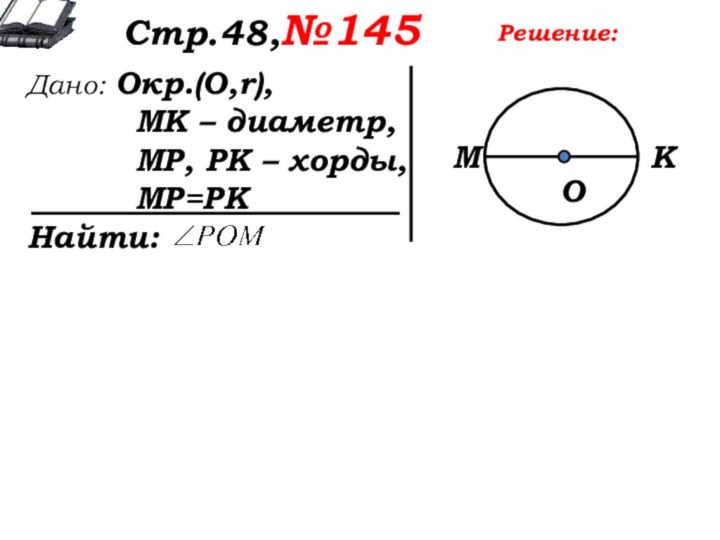
Решение:
∆МРК – равнобедренный, т.к. МР=РК.
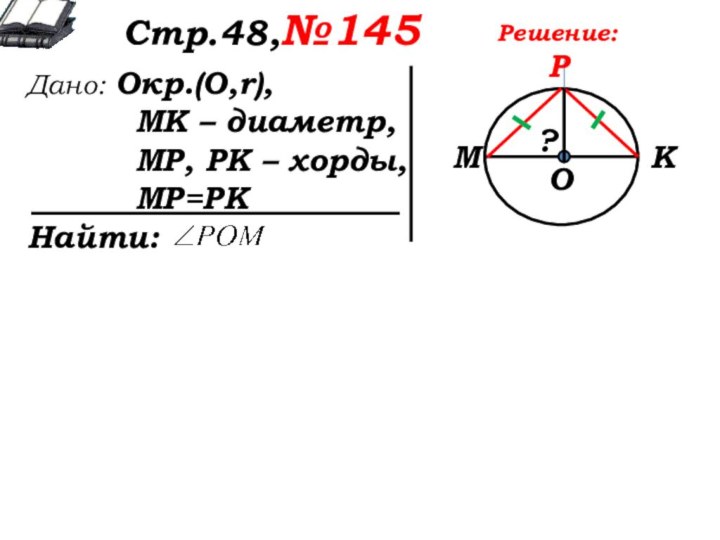
М
К
Р
О
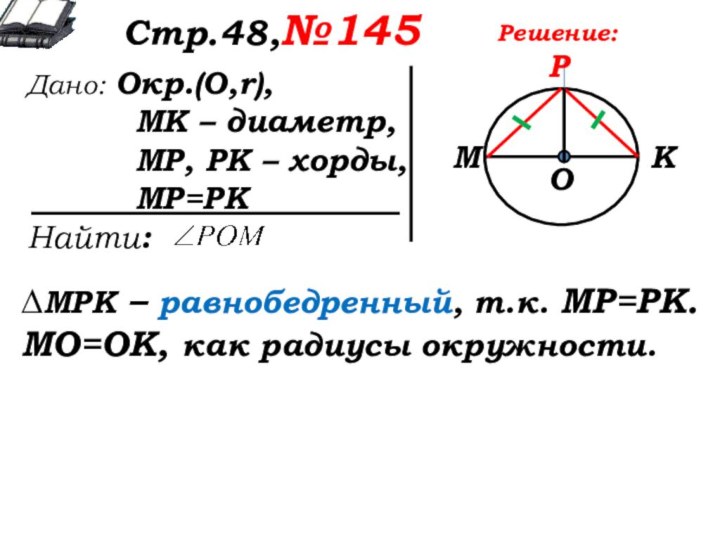
Решение:
∆МРК – равнобедренный, т.к. МР=РК.
МО=ОК, как радиусы окружности.
М
К
Р
О
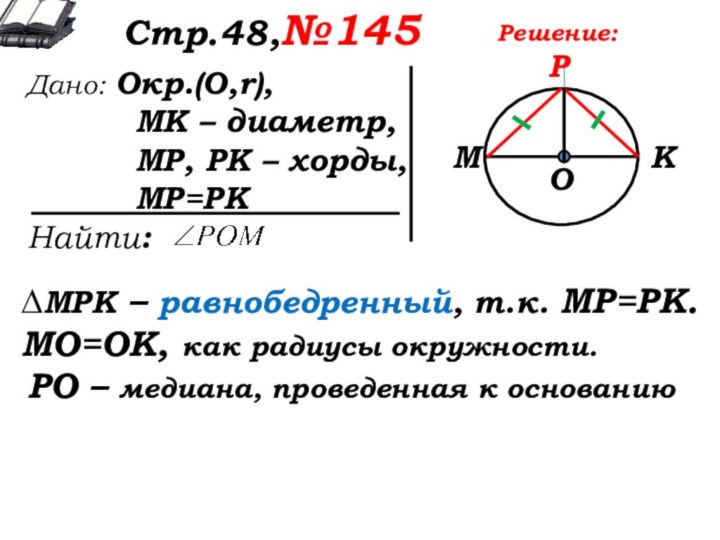
Решение:
∆МРК – равнобедренный, т.к. МР=РК.
МО=ОК, как радиусы окружности.
РО – медиана, проведенная к основанию
М
К
Р
О
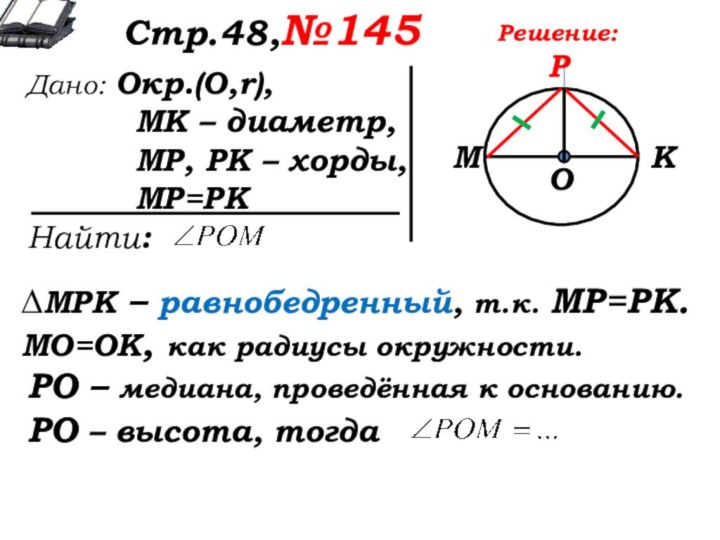
Решение:
∆МРК – равнобедренный, т.к. МР=РК.
МО=ОК, как радиусы окружности.
РО – медиана, проведённая к основанию.
РО – высота, тогда
М
К
Р
О
Решение:
∆МРК – равнобедренный, т.к. МР=РК.
МО=ОК, как радиусы окружности.
РО – медиана, проведённая к основанию.
РО – высота, тогда
Ответ: 90°.
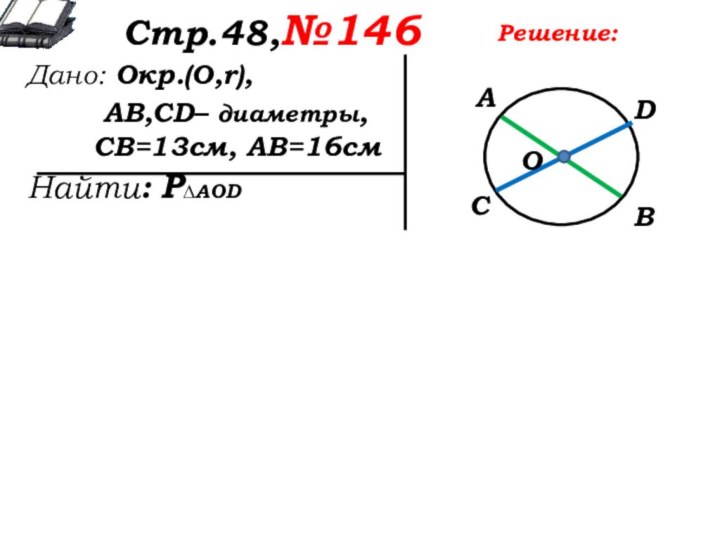
Решение:
А
О
C
D
В
Что нужно найти в задаче?
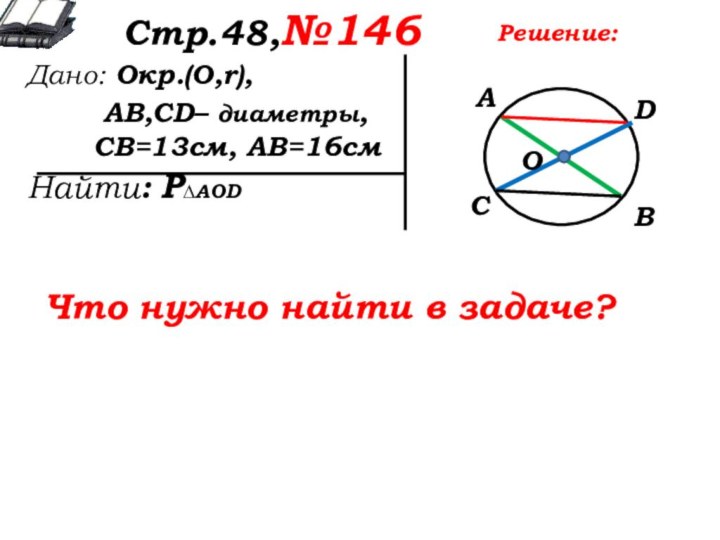
Решение:
А
О
C
D
В
Что для этого нужно знать?
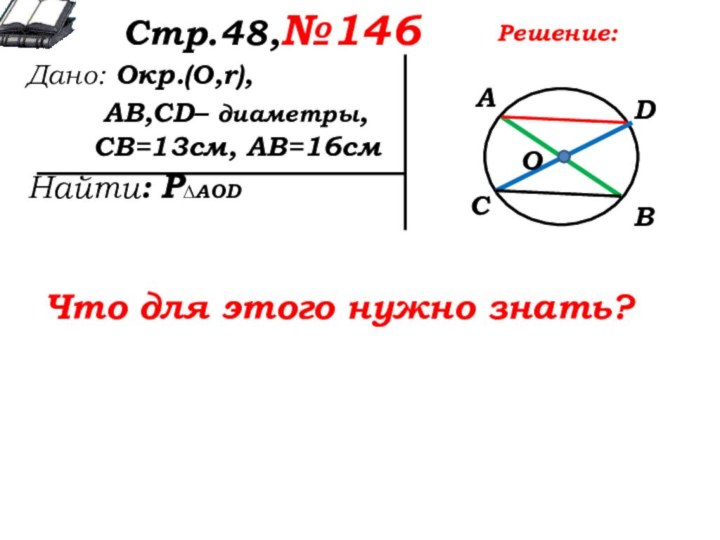
Решение:
А
О
C
D
В
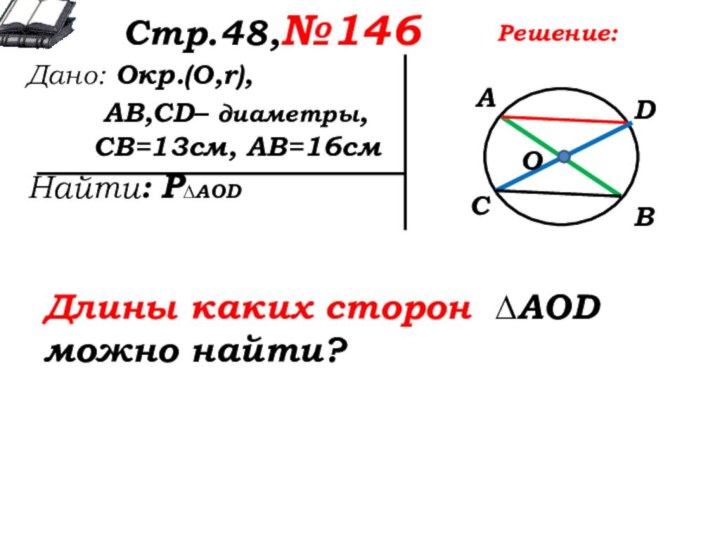
Длины каких сторон ∆AOD можно найти?
Решение:
А
О
C
D
В
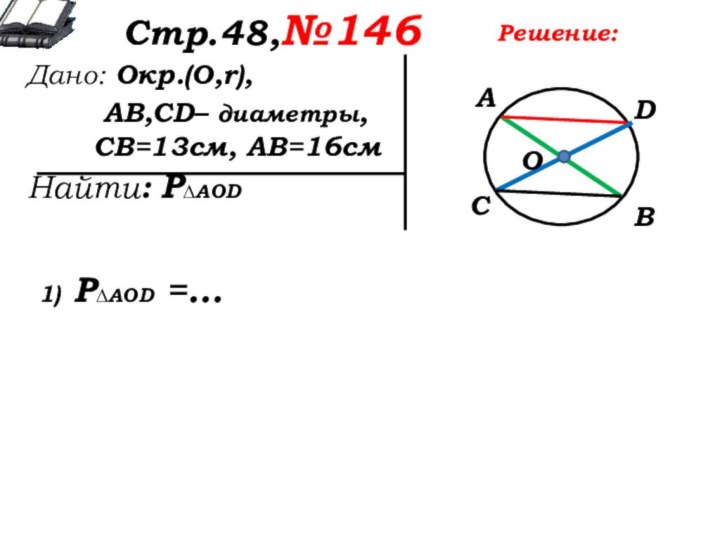
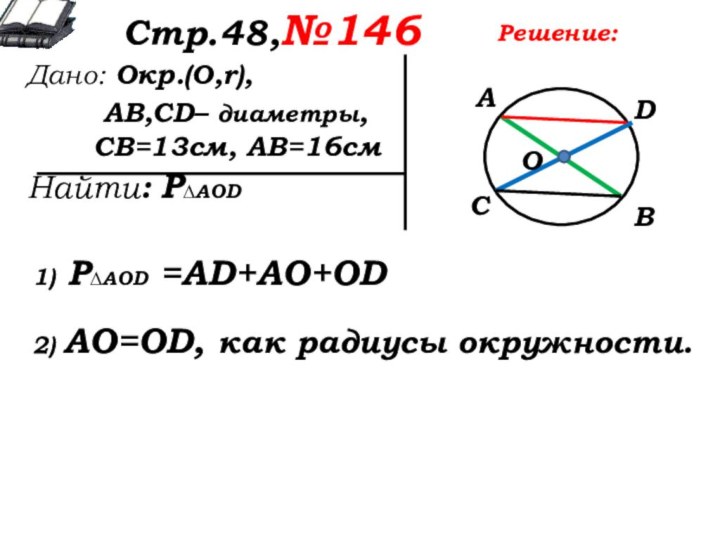
1) Р∆AOD =…
Решение:
А
О
C
D
В
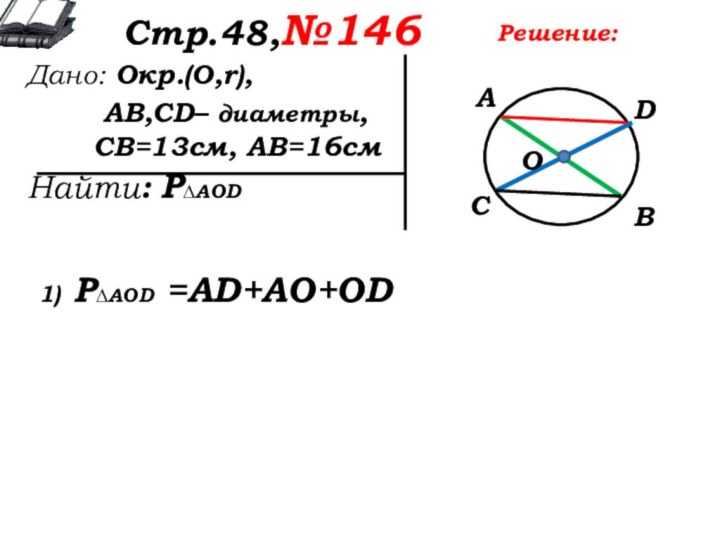
1) Р∆AOD =AD+AO+OD
Решение:
А
О
C
D
В
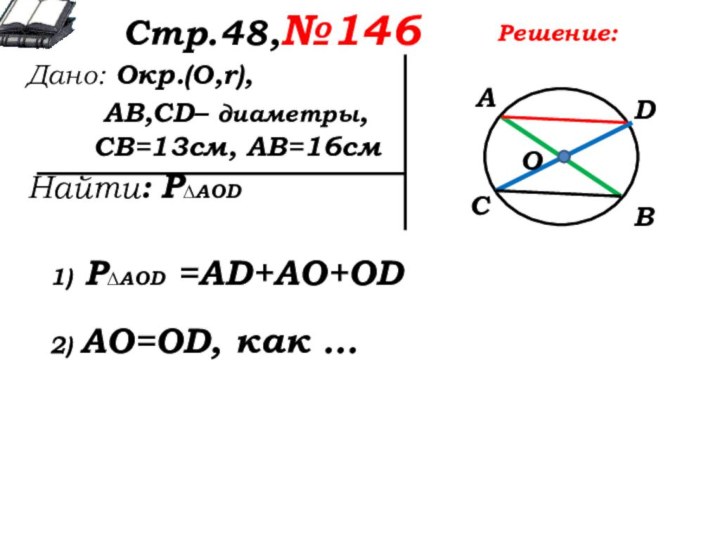
1) Р∆AOD =AD+AO+OD
2) AO=OD, как …
Решение:
А
О
C
D
В
1) Р∆AOD =AD+AO+OD
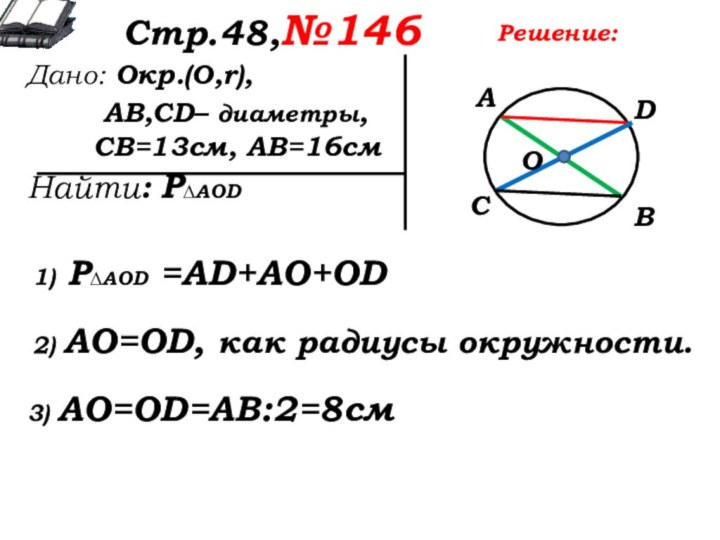
2) AO=OD, как радиусы окружности.
Решение:
А
О
C
D
В
1) Р∆AOD =AD+AO+OD
2) AO=OD, как радиусы окружности.
3) AO=OD=АВ:2=8см
Решение:
А
О
C
D
В
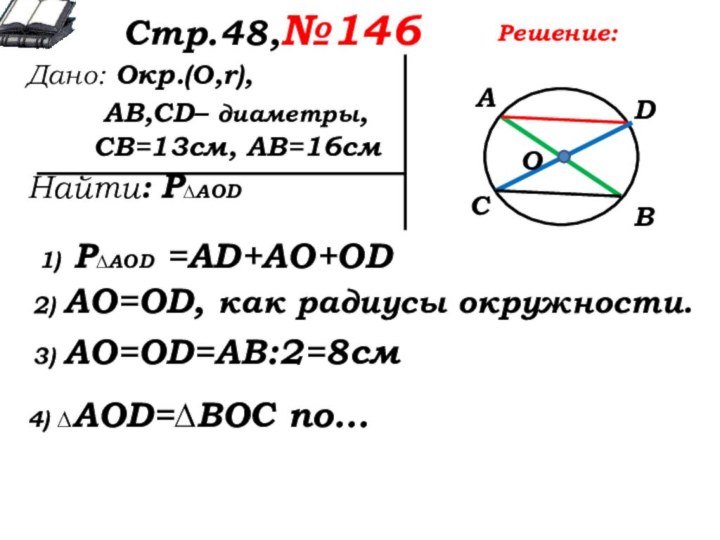
1) Р∆AOD =AD+AO+OD
2) AO=OD, как радиусы окружности.
3) AO=OD=АВ:2=8см
4) ∆AOD=∆ВОС по…
Решение:
А
О
C
D
В
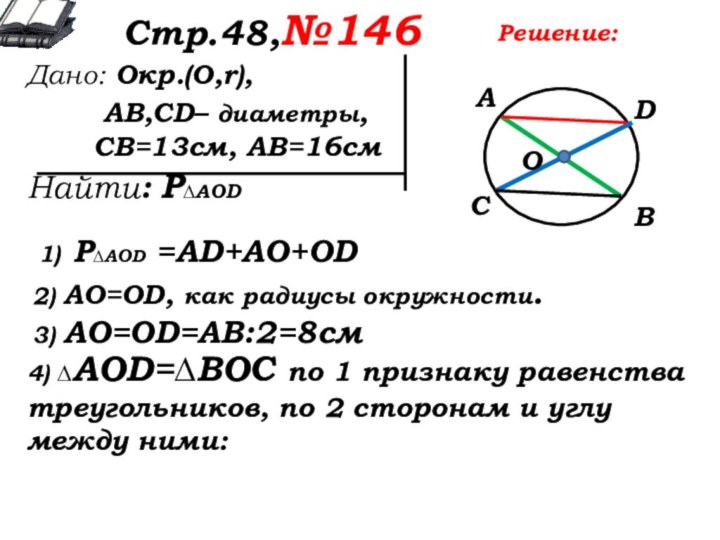
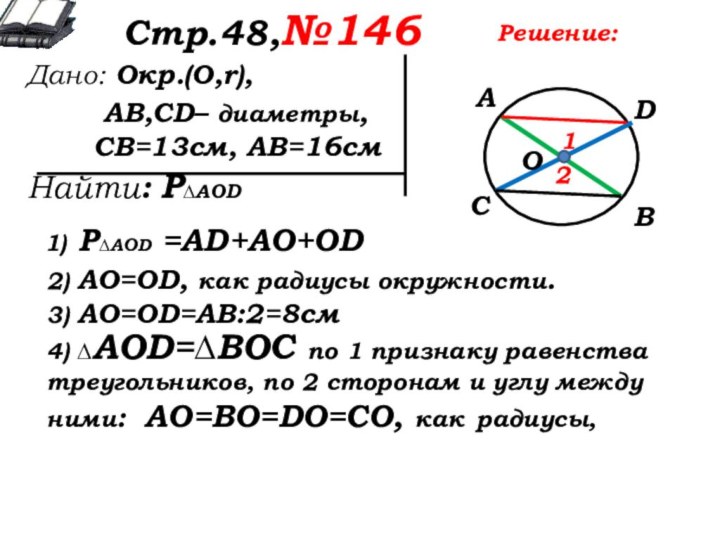
1) Р∆AOD =AD+AO+OD
2) AO=OD, как радиусы окружности.
3) AO=OD=АВ:2=8см
4) ∆AOD=∆ВОС по 1 признаку равенства треугольников, по 2 сторонам и углу между ними:
Решение:
А
О
C
D
В
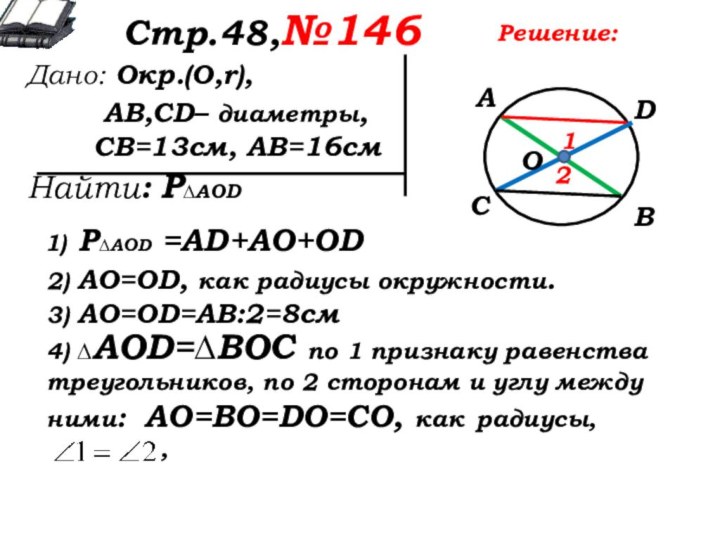
1) Р∆AOD =AD+AO+OD
2) AO=OD, как радиусы окружности.
3) AO=OD=АВ:2=8см
4) ∆AOD=∆ВОС по 1 признаку равенства треугольников, по 2 сторонам и углу между ними: АО=ВО=DO=СО, как радиусы,
1
2
Решение:
А
О
C
D
В
1) Р∆AOD =AD+AO+OD
2) AO=OD, как радиусы окружности.
3) AO=OD=АВ:2=8см
4) ∆AOD=∆ВОС по 1 признаку равенства треугольников, по 2 сторонам и углу между ними: АО=ВО=DO=СО, как радиусы,
,
1
2
Решение:
А
О
C
D
В
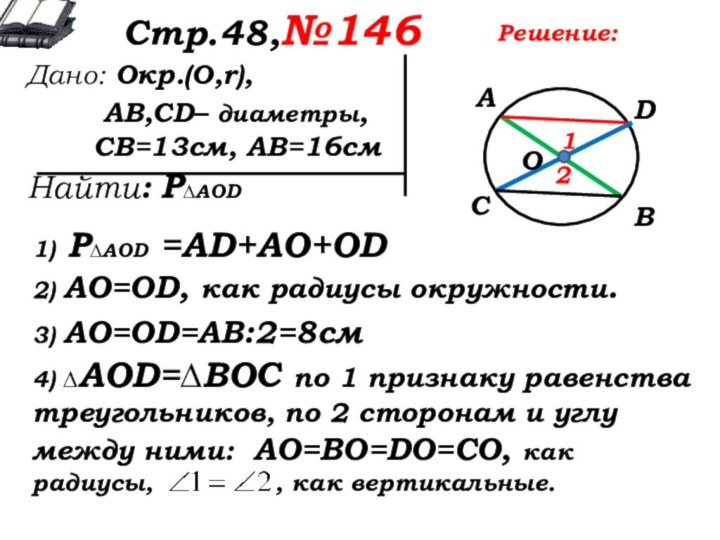
1) Р∆AOD =AD+AO+OD
2) AO=OD, как радиусы окружности.
3) AO=OD=АВ:2=8см
4) ∆AOD=∆ВОС по 1 признаку равенства треугольников, по 2 сторонам и углу между ними: АО=ВО=DO=СО, как радиусы, , как вертикальные.
1
2
Решение:
А
О
C
D
В
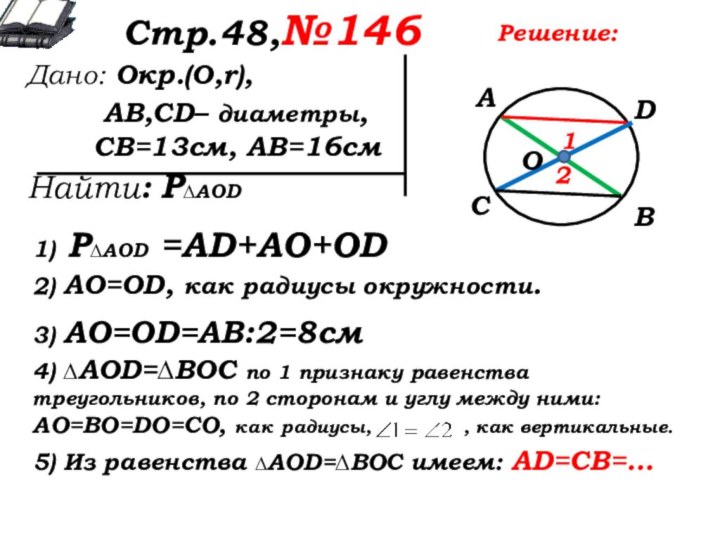
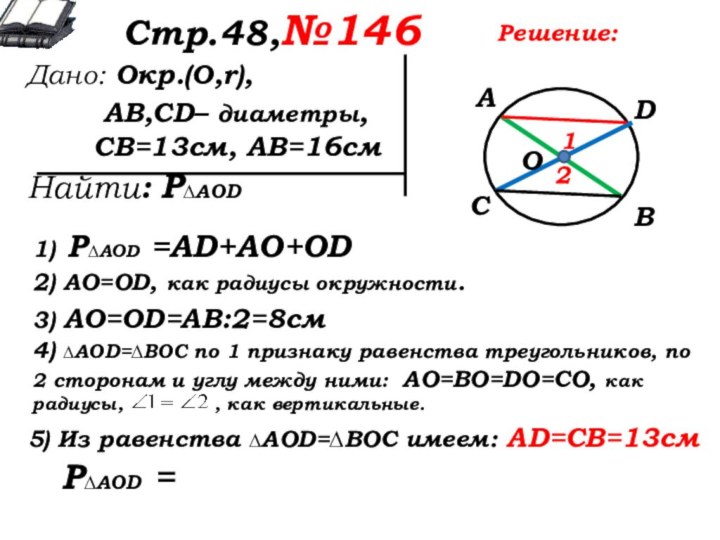
1) Р∆AOD =AD+AO+OD
2) AO=OD, как радиусы окружности.
3) AO=OD=АВ:2=8см
4) ∆AOD=∆ВОС по 1 признаку равенства треугольников, по 2 сторонам и углу между ними: АО=ВО=DO=СО, как радиусы, , как вертикальные.
1
2
5) Из равенства ∆AOD=∆ВОС имеем: AD=CB=…
Решение:
А
О
C
D
В
1) Р∆AOD =AD+AO+OD
2) AO=OD, как радиусы окружности.
3) AO=OD=АВ:2=8см
4) ∆AOD=∆ВОС по 1 признаку равенства треугольников, по 2 сторонам и углу между ними: АО=ВО=DO=СО, как радиусы, , как вертикальные.
1
2
5) Из равенства ∆AOD=∆ВОС имеем: AD=CB=13см
Р∆AOD =
Решение:
А
О
C
D
В
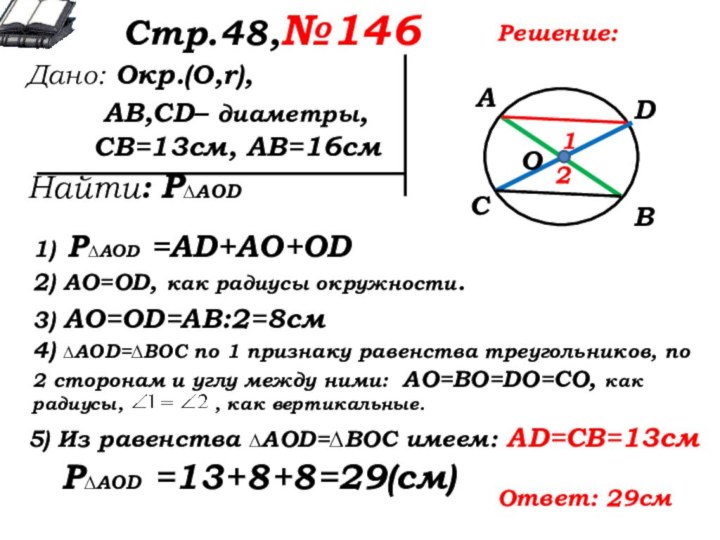
1) Р∆AOD =AD+AO+OD
2) AO=OD, как радиусы окружности.
3) AO=OD=АВ:2=8см
4) ∆AOD=∆ВОС по 1 признаку равенства треугольников, по 2 сторонам и углу между ними: АО=ВО=DO=СО, как радиусы, , как вертикальные.
1
2
5) Из равенства ∆AOD=∆ВОС имеем: AD=CB=13см
Р∆AOD =13+8+8=29(см)
Ответ: 29см