Слайд 2
ДАТЫ ЖИЗНИ И ДЕЯТЕЛЬНОСТИ АПОЛЛОНИЯ
Ок. 250 до н.
э. Родился в Перге в Малой Азии.
Ок. 235—225 до
н. э. Учился в Эфесе у Евдема Пергамского.
Ок. 225—215 до н. э. Учился в Александрии у учеников Евклида.
Разработал теорию движения Солнца, Луны и планет по деферен-
там и эпициклам.
Ок. 215—195 до н. э. Писал «Конические сечения» в Александрии.
Посетил Евдема Пергамского в Пергаме и послал ему I—III книги
«Конических сечений».
После смерти Евдема Пергамского
послал
остальные книги «Конических сечений»
его ученику Атталу.
Ок. 170 до н. э. Умер.
Слайд 3
Аполлоний древнегреческий математик, один из трёх (наряду с Евклидом и Архимедом)
великих геометров античности.
Аполлоний прославился в первую очередь монографией «Конические
сечения» (8 книг), в которой дал содержательную общую теорию эллипса, параболы и гиперболы. Именно Аполлоний предложил общепринятые названия этих кривых; до него их называли просто «сечениями конуса».
Он ввёл и другие математические термины, латинские аналоги которых навсегда вошли в науку, в частности: асимптота, абсцисса, ордината, аппликата.
Слайд 4
Титульные листы изданий «Конических сечения»
Слайд 5
Аполлоний первый рассматривал эллипс, параболу и гиперболу как
произвольные плоские сечения произвольных конусов с круговым основанием и
детально исследовал их свойства. Обнаружил, что парабола — предельный случай эллипса, открыл асимптоты гиперболы; получил (в словесной форме) уравнение параболы; впервые изучал свойства касательных и подкасательных к коническим сечениям.
Аполлоний доказал 387 теорем о кривых 2-го порядка методом, который состоял в отнесении кривой к какому-либо ее диаметру и к сопряженным с ним хордам, и предвосхитил созданный в XVII в. метод координат.
Все соотношения Аполлоний рассматривал как отношения равновеликости между некоторыми площадями. “Конические сечения” Аполлония оказали большое влияние на развитие астрономии, механики, оптики. Из положений Аполония исходили при создании аналитической геометрии Р. Декарт и П. Ферма.
Слайд 6
Из других заслуг Аполлония перед наукой отметим, что
он переработал астрономическую модель Евдокса, введя эпициклы и эксцентрики для объяснения неравномерности
движения планет. Эту теорию позднее развили Гиппарх и Птолемей.
Известны задача Аполлония о нахождении круга, касающегося трех данных кругов, теорема Аполлония и окружность Аполлония.
Слайд 7
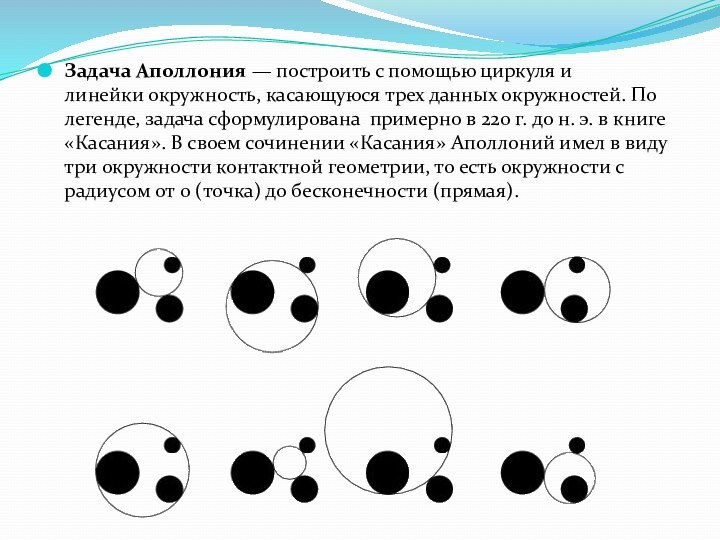
Задача Аполлония — построить с помощью циркуля и линейки окружность, касающуюся
трех данных окружностей. По легенде, задача сформулирована примерно в 220 г.
до н. э. в книге «Касания». В своем сочинении «Касания» Аполлоний имел в виду три окружности контактной геометрии, то есть окружности с радиусом от 0 (точка) до бесконечности (прямая).
Слайд 8
Таким образом, для задачи Аполлония существует 10 глобальных

случаев:
построить с помощью циркуля и линейки окружность, касающуюся трех
точек.Решение: Соединим эти точки. Проведем к получившимся отрезкам серединные перпендикуляры. Они пересекутся в одной точке. Эта точка — центр искомой окружности.
построить с помощью циркуля и линейки окружность, касающуюся двух точек (далее Α и Β) и прямой (далее а). Сначала проведем прямую ΑΒ. Решение:
Если АВ не параллельна а, то найдем их пересечение С. Построим среднее геометрическое отрезков ΑС и ΒС. Отложим равный ему отрезок СΚ на прямой а. Окружность, описанная около ΔΑΒΚ — искомая.
Если ΑΒ||а, то проведем серединный перпендикуляр к отрезку ΑΒ и отметим точку Κ его пересечения с прямой a. Окружность, описанная около ΔΑΒΚ — искомая.
построить с помощью циркуля и линейки окружность, касающуюся точки и двух прямых. Решение:
Если прямые не параллельны, то возьмем точку их пересечения. Назовем угол между этими прямыми α. Соединим точку пересечения прямых с заданой точкой Μ. Назовем получившийся отрезок а. Впишем в угол α произвольную окружность, которая пересечет а, и отметим её центр Ο и точку пересечения с а (каждая даст свое решение) Α. Проведем прямую ΑΟ. Проведем параллельную ей прямую через Μ и биссектрису угла α. Их пересечение будет центром искомой окружности. Если прямые параллельны, построим прямую ΑΒ (Α и Β — точки пересечения с задаными прямыми), перпендикулярную им. Проведем к отрезку ΑΒ серединный перпендикуляр b. Проведем окружность с центром в заданой точке и радиусом, равным половине ΑΒ. Её пересечение с b будет центром искомой окружности.
построить с помощью циркуля и линейки окружность, касающуюся трех прямых.Решение:
Если среди них нет параллельных, то отметим точки их пересечения Α, Β и С. Окружность, вписанная в ΔΑΒС — искомая.
Если все три прямые параллельны друг другу, то окружности не существует.
построить с помощью циркуля и линейки окружность, касающуюся двух точек (далее Α и Β) и окружности (далее ω).
Если А и В не лежат на ω, то проведем окружность Ω, содержащую точки А и В и имеющую с ω общие точки. Проведем радикальную ось Ω и ω и пересечем её с АВ. Проведем из точки их пересечения касательную к ω и отметим точку касания Κ. Опишем окружность около ΔΑΒΚ. Она — искомая. Каждая касательная даст свое решение.
Если А и В лежат на ω, ω — искомая.
построить с помощью циркуля и линейки окружность, касающуюся точки и двух окружностей.
построить с помощью циркуля и линейки окружность, касающуюся двух прямых и окружности.
построить с помощью циркуля и линейки окружность, касающуюся прямой и двух окружностей.
построить с помощью циркуля и линейки окружность, касающуюся точки, прямой и окружности.
построить с помощью циркуля и линейки окружность, касающуюся трех окружностей.
Слайд 9
Теорема Аполлония
В планиметрии теорема Аполлония является формулой, выражающей длину медианы треугольника через его стороны.
В частности, если в каком-либо треугольнике ABC медиана AD, то
Слайд 10
Доказательство
Пусть стороны треугольника a, b, c, а медиана d проведена к стороне
a треугольника. Пусть m —
длина отрезков a, образованных медианой, то есть m составляет половинуa. Пусть углы
между a и d — θ и θ′, где θ содержит b и θ′ содержит c. Затем, θ′ является смежным углом к θ и cos θ′ = −cos θ. Теорема косинусов для θ и θ′ гласит:
Сложив эти уравнения, получим
Слайд 11
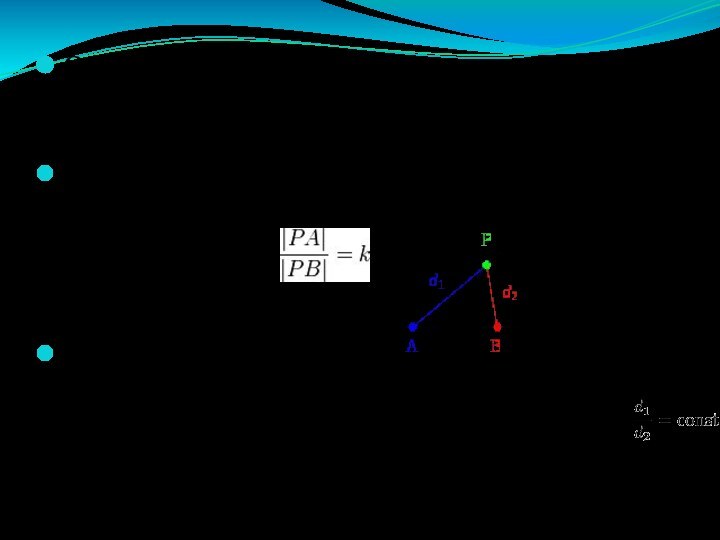
Окружность Аполлония — геометрическое место точек плоскости, отношение расстояний от которых
до двух заданных точек — величина постоянная, не равная единице.
Пусть
на плоскости даны две точки А и В. Рассмотрим все точки Р этой плоскости, для каждой из которых
где k — фиксированное
положительное число.
При k = 1 эти точки
заполняют срединный
перпендикуляр к отрезку ;
в остальных случаях указанное геометрическое место — окружность, называемая окружностью Аполлония.
Слайд 12
Свойства:
Радиус окружности Аполлония
Отрезок РС между точкой на окружности и точкой
пересечения ее с прямой АВ является биссектрисой самого угла АРВ или
угла, смежного с ним.
Центр данной окружности лежит на прямой, соединяющей эти две точки.
Слайд 13
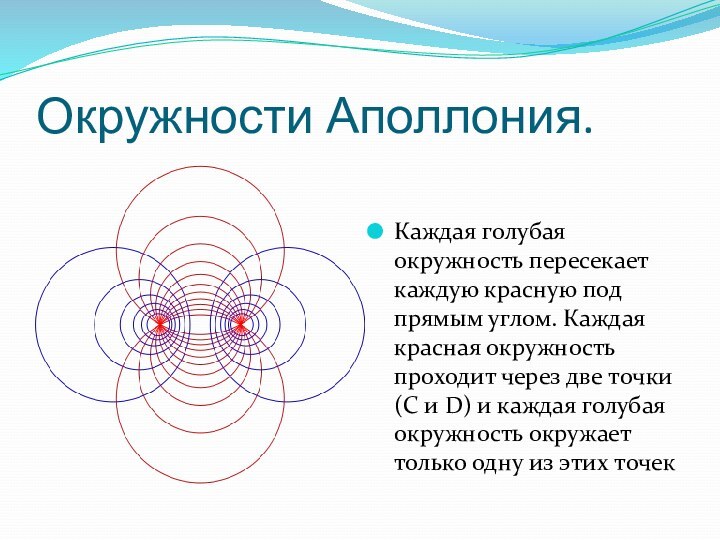
Окружности Аполлония.
Каждая голубая окружность пересекает каждую красную под
прямым углом. Каждая красная окружность проходит через две точки
(C и D) и каждая голубая окружность окружает только одну из этих точек
Слайд 14
В VII книге Математического собрания Папп дает краткое описание шести математических
трактатов Аполлония:
Отсечение отношения (Λογου αποτομη) в двух книгах, содержащих 180
теорем
Отсечение площади (Χωριου αποτομη) в двух книгах, содержащих 124 теоремы.
Определенное сечение (Διωριςμενη τομη) в двух книгах, содержащих 83 теоремы.
Вставки (Νευσεις) в двух книгах, содержащих 125 теорем.
Касания (Επαφαι) в двух книгах, содержащих 60 теорем.
Плоские места (Τοποι επιπεδοι) в двух книгах, содержащих 147 теорем.
В других трудах Папп упоминает ещё несколько сочинений Аполлония:
Числа.
О неупорядоченных иррациональностях.
Слайд 15
Прокл Диадох в Комментарии к I книге Начал Евклида упоминает трактат
Аполлония
О Винтовых линиях (Περι του κοχλιου). Предположительно здесь рассматривались спирали
на поверхности цилиндра.
Так называемая XIV книга Начал Евклида, написанная Гипсиклом, представляет собой комментарий к сочинению Аполлония
Сравнение додекаэдра с икосаэдром. Аполлоний доказывает, что поверхности додекаэдра и икосаэдра, вписанных в одну и ту же сферу, относятся так же, как их объёмы.
Евтокий в комментариях к Измерению круга Архимеда упоминает сочинение Аполлония
Быстрое получение результатов. (Ωκυτοκιον). Здесь Аполлоний соревнуется с Архимедом. Он описывает более удобную, чем у Архимеда, систему именования очень больших чисел, а также более быстрый, чем предложенный Архимедом, алгоритм вычисления отношения длины окружности к её диаметру.
Слайд 16
Труды Аполлония оказали огромное влияние на творчество последующих
математиков, включая Ферма, Декарта, Ньютона, Лагранжа и многих других. Многие теоремы Аполлония, особенно
о максимумах, эволютах, нормалях и т. п. вошли в современные учебники по дифференциальной геометрии конических сечений.
Каким образом Аполлоний, не владея математическим анализом, сумел сделать свои открытия, неясно.
Ван дер Варден пишет:
Аполлоний виртуозно владеет геометрической алгеброй, но не менее виртуозно умеет скрывать свой первоначальный ход мыслей. Из-за этого-то его книги и трудно понимать; рассуждения его элегантны и кристально ясны, но что его привело именно к таким рассуждениям, а не к иным каким-нибудь,— об этом можно лишь догадываться.