Слайд 2
Понятие «аппроксимация функции»
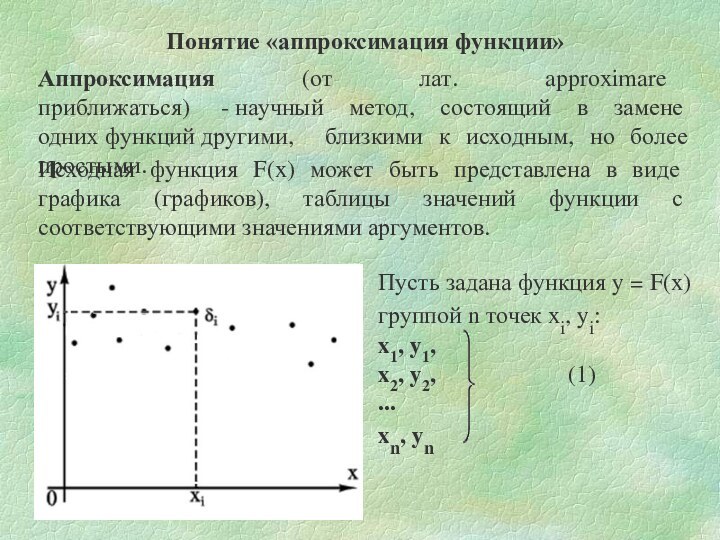
Пусть задана функция y = F(x)
группой n точек xi, yi:
x1, y1,
x2, y2,
(1)
...
xn, yn
Аппроксимация (от лат. approximare приближаться) - научный метод, состоящий в замене одних функций другими, близкими к исходным, но более простыми.
Исходная функция F(x) может быть представлена в виде графика (графиков), таблицы значений функции с соответствующими значениями аргументов.
Слайд 3
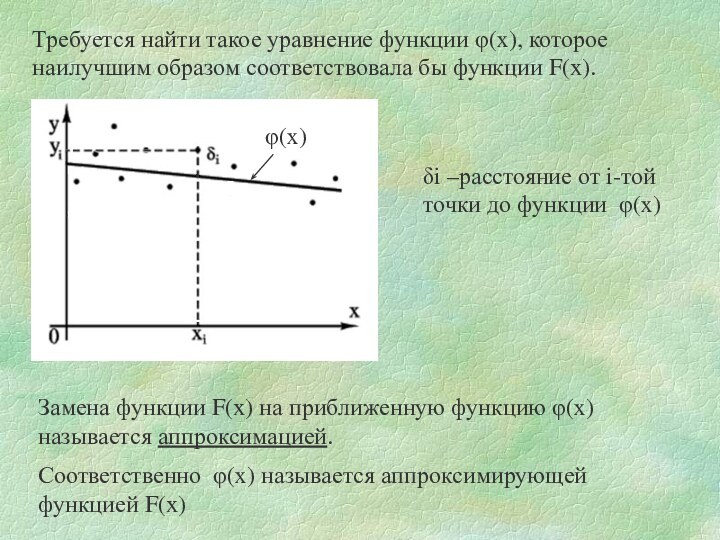
Соответственно φ(х) называется аппроксимирующей функцией F(x)
δi –расстояние от
i-той точки до функции φ(х)
Замена функции F(x) на
приближенную функцию φ(х) называется аппроксимацией.
Требуется найти такое уравнение функции φ(х), которое наилучшим образом соответствовала бы функции F(x).
Слайд 4
На практике применяются полиномы более простого вида:
φ(х)
= a0+a1x+a2x2+...+anxn - для однопараметрической зависимости;
φ(х) =
a0+a1x1+a2x2+...+anxn - для многопараметрической зависимости;
φ(х) = a0+a1x1+a2x2+...+anxn+
+a12x1x2+a13x1x3+…+a(n-1)nxn-1xn+
+a11x12+a22x22+…+annxn2 - для многопараметрической зависимости с учетом парных взаимодействий,
где a0, a1, a2, ... , an – являются неизвестными коэффициентами уравнения, которые определяются методом наименьших квадратов (МНК).
φ(х) = а0 + a1x1 + a2x2 + ....+ a kxk + a12x1x2 + a13x1x3 + .... + ak,k-1 xkxk-1 +…. + a11x212 + a22x222 + .... + akkx2k2 + ....
Функцию φ(х) можно представить в виде ряда Тейлора:
Слайд 5
Суть метода наименьших квадратов
Рассмотрим применение МНК в случае
применения линейного полинома:
φ(х) = y = a + bx
(2)
Пусть мы нашли такую прямую.
Обозначим через δi расстояние точки xi от этой прямой, измеренное параллельно оси y.
Слайд 6
Из уравнения (2) следует, что
(3)
Чем меньше числа δi по абсолютной величине, тем лучше подобрана прямая (2). В качестве характеристики точности подбора прямой (2) можно принять сумму квадратов:
(4)
Покажем, как можно подобрать прямую (2) так, чтобы сумма квадратов SS была минимальной.
Из уравнений (3) и (4) получаем:
(5)
Слайд 7
Условия минимума SS будут:
(6)
(7)
Уравнения (6) и (7) можно записать в таком виде:
(8)
(9)
Слайд 8
Из уравнений (8) и (9) определяют неизвестные коэффициенты
а и b:
;
Слайд 9
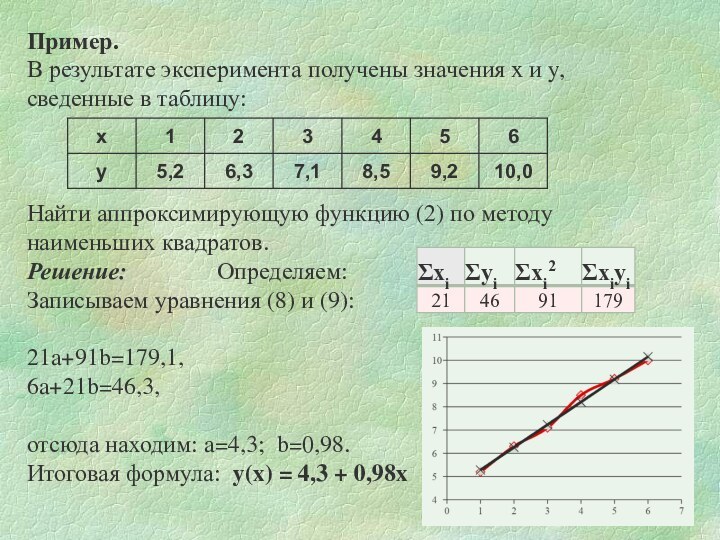
Пример.
В результате эксперимента получены значения x и y,
сведенные в таблицу:
Найти аппроксимирующую функцию (2) по методу
наименьших квадратов.
Решение: Определяем:
Записываем уравнения (8) и (9):
21a+91b=179,1,
6a+21b=46,3,
отсюда находим: a=4,3; b=0,98.
Итоговая формула: y(x) = 4,3 + 0,98x
Слайд 11
φ(х) = a0+a1x1+a2x2+...+akxk+
+a12x1x2+a13x1x3+…+a(k-1)kxk-1xk
(10)
Если необходимо учитывать парные
взаимодействия параметров, то, как правило, применяется линейный полином следующего вида:
Введем следующие обозначения:
а12 = ak+1; x1x2 = xk+1;
а13 = ak+2; x1x3 = xk+2;
……………………….
аp = am; xp-1xp = xm
Тогда уравнение (10) можно записать в следующем виде:
φ(х) = yp = a0x0+a1x1+a2x2+...+akxk+ ak+1xk+1+…+ amxm=
где х0 – фиктивное переменное, равное 1.
Многопараметрическая аппроксимация
Слайд 12
Пусть в каждой узловой точке проведено по одному
опыту. Рассмотрим таблицу экспериментальных данных, содержащую N строк:
где k
– счетчик количества входных параметров;
u – счетчик количества узловых точек эксперимента, u=1, 2,…, N;
N – число узловых точек, а также число опытов;
i – счетчик количества членов регрессии, i=1,2,…, m;
Для этих же целей потребуется еще один счетчик – j=1,2,…, m.
Слайд 13
Для нахождения неизвестных a0, a1,…, am нужно определить
частные производные суммы квадратов:
…
SS=[(y1-a0x01-a1x11-…-amxm1)2+ (первая строка таблицы)
+ (y2-a0x02-a1x12-…-amxm2)2+ (вторая строка таблицы)
……………………………..
+(yN-a0x0N-a1x1N-…-amxmN)2] (N-ая строка таблицы)
В качестве примера рассмотрим частную производную по а0 только от первой строки:
2a0x01x01+2a1x01x11+2a2x01x21+…+2amx01xm+1-2x01y1
Слайд 14
Проведем суммирование по всем строкам, затем выполним аналогичные
действия по другим производным и получим систему нормальных уравнений:
Слайд 15
Для упрощения записи системы нормальных уравнений введем обозначения:
Тогда
матрицы (ij) и (jy) примут следующий вид:
где индекс i
определяет номер столбца, а j – номер строки.
Матрица (ij) называется нормальной или информационной.
Она является квадратной и симметричной.
(jy) – это столбец свободных членов.
Слайд 16
После этого систему нормальных уравнений можно записать в
матричной форме следующим образом:
(ai)(ij)=(jy) ,
(11)
где (ai) – стока неизвестных (коэффициентов регрессии).
Систему (11) можно решить с помощью обратной матрицы (Сij):
Тогда неизвестные аi можно рассчитать по формуле:
Слайд 17
Т.е. для нахождения коэффициента ai нужно все элементы
i-того столбца перемножить на элементы соответствующей строки матрицы (ij).
Например:
a1 = C01(0y) + C11(1y)+ … + Cm1(my) =
Слайд 18
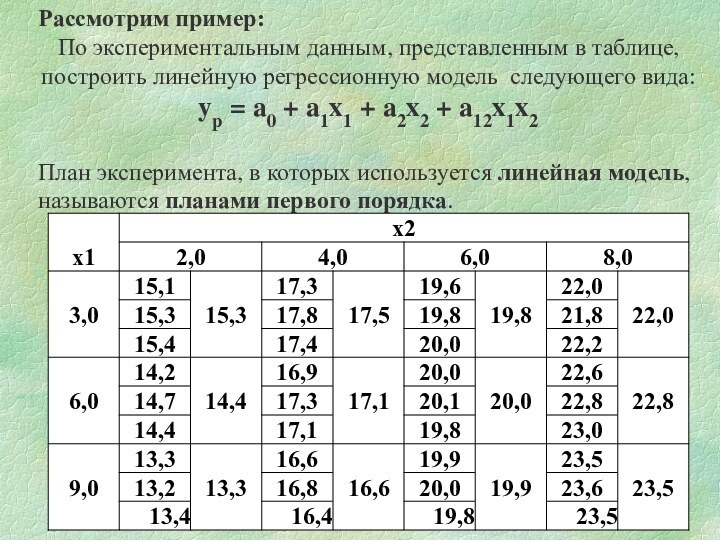
Рассмотрим пример:
По экспериментальным данным, представленным в таблице, построить
линейную регрессионную модель следующего вида: yp
= a0 + a1x1 + a2x2 + a12x1x2
План эксперимента, в которых используется линейная модель, называются планами первого порядка.
Слайд 19
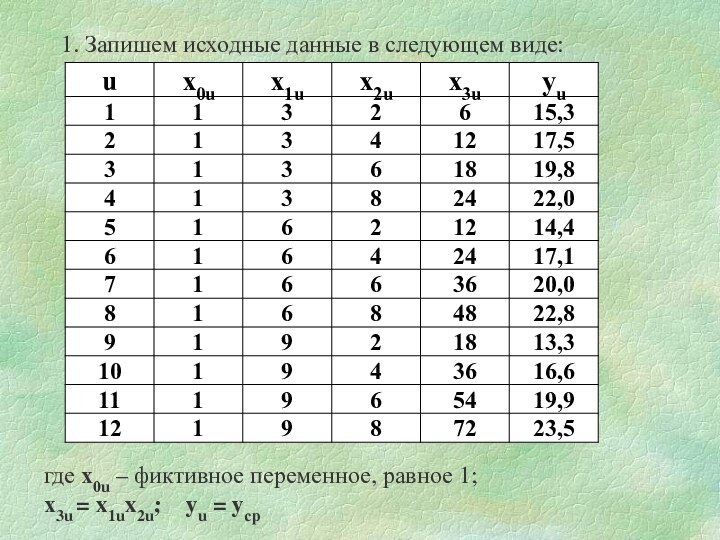
1. Запишем исходные данные в следующем виде:
где х0u
– фиктивное переменное, равное 1;
х3u = x1ux2u;
yu = yср
Слайд 20
2. Построим матрицы (ij) и (jy):
где компоненты матрицы
(ij) рассчитываются следующим образом:
При использовании Excel для определения компонентов
матрицы (ij) целесообразно применять функцию =СУММПРОИЗВ.
Слайд 21
где компоненты матрицы (jy) рассчитываются следующим образом:
Слайд 22
3. Построим обратную матрицу (Сij) с помощью Excel.
Сначала
следует убедится, что определитель матрицы (ij) не равен 0.
В противном случае нельзя построить обратную матрицу.
Определитель рассчитываем с помощью функции =МОПРЕД.
Определитель = 18662400
Компоненты матрицы (Сij) рассчитываются с помощью функции =МОБР.
Эта функция первоначально отображает только первый компонент матрицы. Поэтому далее следует выделить интервал ячеек, начиная с первоначальной ячейки, в которых будут выведены остальные компоненты матрицы (Сij). После этого нажать клавишу F2 и далее сочетание клавиш Contr+Shift+Enter.
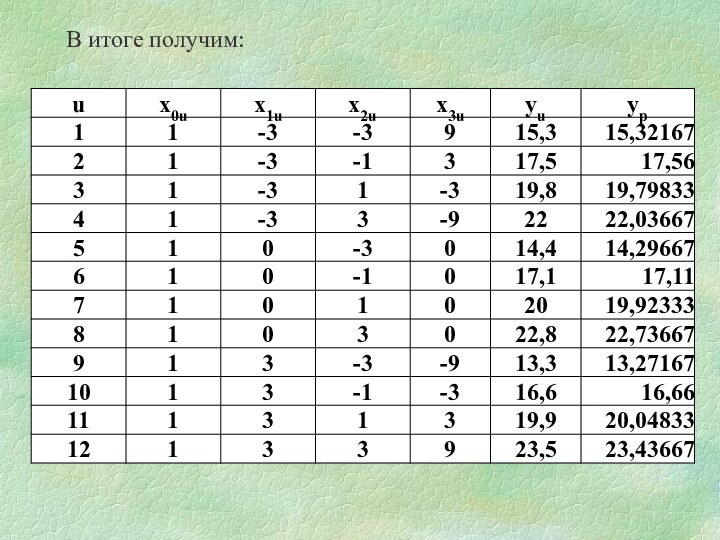
Слайд 23
В итоге получим:
4. Рассчитаем коэффициенты регрессии по формуле:
Например:
a0
= 3,5*222,2-0,5*1329,3-0,583*1194,4+0,0833*7187,4=14,68
Остальные коэффициенты регрессии равны:
Слайд 24
5. Запишем итоговую формулу и проведем расчеты:
yp =
14,68333 -0,53333*x1 + 0,831667*x2 + 0,095833*x1*x2
Слайд 25
Однако полученное решение не является идеальным, т.к. недиагональные
компоненты обратной матрицы Сij не равны 0, что приводит
к ошибке вычислений.
Количественной мерой оценки ошибки вычислений служит коэффициент ковариации ρ(ai, aj):
ρ(ai, aj) меняется от -1 до +1.
Если ρ(ai, aj) = 0, то ошибка вычислений ai не влияет на вычисление aj.
Чем ближе ρ(ai, aj) к -1, либо +1, тем больше это влияние.
Слайд 26
В рассмотренной задаче ρ(ai, aj) равны:
Пример расчета ρ(a0,
a1) = -0,5/(3,5+0,083)0,5 = -0,925
Следовательно, рассмотренный план эксперимента
не является оптимальным.
Матрица (Сij) также называется матрицей ошибок, т.к. точность вычисления коэффициентов регрессии ai зависит от значений ее элементов.
В этой связи, эффективными планами являются так называемые рототабельные и ортогональные планы.
Слайд 27
Рототабельные планы
Точность эмпирических формул, полученных по методике планирования
эксперимента, зависит от равномерности расположения узловых точек относительно центра
плана эксперимента. Равномерность такого распределения можно оценить с помощью дисперсии расчетного значения yp, которая равна:
Дисперсия S2(ypu) представляет собой эллипсоид, который называется эллипсоидом рассеяния. Чем меньше эллипсоид рассеяния, тем с большей точностью расчетное значение ypu совпадает с экспериментальным yu.
Планы, которые требуют, чтобы рассеяние по всем осям было одинаковым, называется рототабельными. Они достигаются при определенных соотношениях элементов в матрице ошибок.
Слайд 28
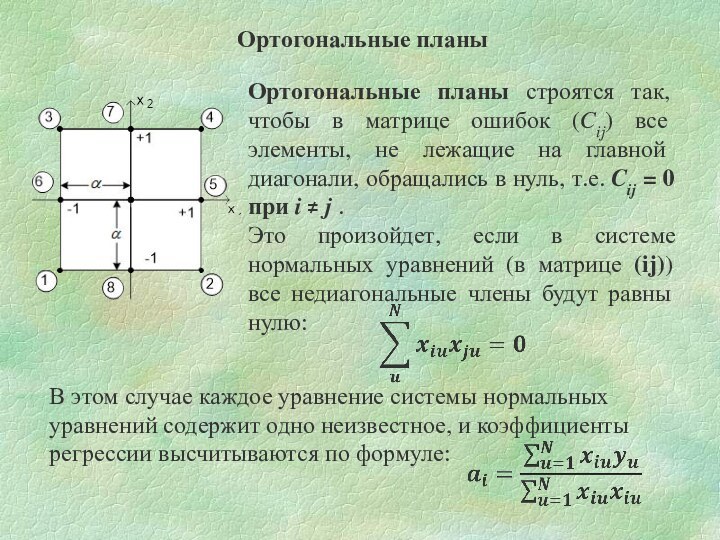
Ортогональные планы
Ортогональные планы строятся так, чтобы в матрице
ошибок (Cij) все элементы, не лежащие на главной диагонали,
обращались в нуль, т.е. Cij = 0 при i ≠ j .
Это произойдет, если в системе нормальных уравнений (в матрице (ij)) все недиагональные члены будут равны нулю:
В этом случае каждое уравнение системы нормальных уравнений содержит одно неизвестное, и коэффициенты регрессии высчитываются по формуле:
Слайд 29
Чтобы план первого порядка стал ортогональным, необходимо выполнить
три условия:
эксперимент должен быть полным факторным и в
каждой узловой точке такого эксперимента должно быть проведено по одному опыту; если в некоторых точках проведено несколько опытов, то в расчетах должны использоваться средние значения;
по каждому фактору x1 , x2 , . . . , xk уровни изменения факторов должны быть равноотстоящими, то есть расстояния между уровнями Δxi = const;
оси координат факторов должны быть перенесены в центр эксперимента путем замены переменных.
Слайд 30
Фактор x1 изменяется на трех уровнях, принимая значения
3,0; 6,0 и 9,0.
Фактор x2 имеет четыре уровня
– 2,0; 4,0; 6,0 и 8,0 .
В каждой точке проведено по три опыта. Итого имеем 12 экспериментальных точек и 36 опытов.
Для рассмотренного примера на рисунке графически представлен полный двухфакторный эксперимент первого порядка с равноотстоящими уровнями.
Слайд 31
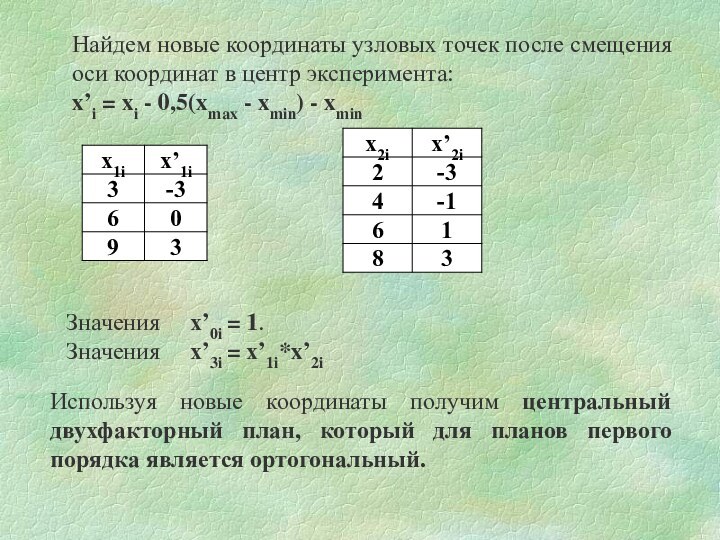
Найдем новые координаты узловых точек после смещения оси
координат в центр эксперимента:
x’i = xi - 0,5(xmax -
xmin) - xmin
Значения х’0i = 1.
Значения х’3i = х’1i*x’2i
Используя новые координаты получим центральный двухфакторный план, который для планов первого порядка является ортогональный.
Слайд 32
Таблица исходных данных с преобразованными координатами узловых точек
выглядит следующим образом:
Слайд 33
Тогда матрицы (ij) и (jy) примут следующий вид:
Коэффициенты
регрессии соответственно равны:
Например, а0 = 222/12=18,51667;
Например, (12) =
6 + 2 – 2 – 6 + 0 – 6 – 2 + 2 + 6 = 0;
(1y) = – 3 * 15,3 – 3 * 17,5 + . . . + 3 * 23,5 = – 3,9 .
Слайд 35
Планы 2k
Особое место в теории планирования эксперимента занимают
полные факторные эксперименты 2k , в которых каждый из
k факторов изменяется только на двух уровнях.
Для построения полного факторного эксперимента 2k:
1. Перенесем оси координат в центр эксперимента, т.е. сделаем план центральным.
2. Создадим два возможных уровня каждого из факторов в новых координатах: xi = + 1 и xi = – 1.
Например, при k=2 полный факторный эксперимент содержит N=22 = 4 узла с координатами х1 и х2:
Слайд 36
В планах 2k обычно единицу не записывают, поскольку
при расчетах важным оказывается только знак при ней.
Тогда
план 22 можно оформить следующей таблицей:
где х0 всегда = +1;
х1х2 = х3
Для эксперимента 22 уравнение
yр = a0 + a1 x1 + a2 x2 + a12 x1 x2 ,
содержащее 4 члена, оказывается адекватным (m = N).
Поскольку план ортогонален, то коэффициенты регрессии легко вычисляются по формуле:
Слайд 37
Например:
;
Как видно, в числителе знаки столбца xi приписываются
к значениям yu , а в знаменателе оказывается число
N .
Найдем коэффициенты регрессии для следующего плана 22:
Слайд 38
Построим для ранее рассмотренного примера план 22
Тогда план
эксперимента 22 можно представить следующим образом:
Расcчитаем коэффициенты ai:
a0 =
(23,5+13,3+22+15,3)/4 = 18,525;
a1 = (23,5+13,3-22-15,3)/4 = -0,125;
a2 = (23,5-13,3+22-15,3)/4 = 4,225;
a3 = (23,5-13,3-22+15,3)/4 = 0,875
Нам понадобится всего четыре эксперимента.
Заменим старые координаты новыми:
Слайд 39
В итоге получим:
Таким образом, план 22 позволил получить
точный результат с помощью четырех экспериментов вместо первоначальных 12
экспериментов.
Слайд 40
Центральный композиционный план
Применяется, если аппроксимируемые функции не являются
линейными.
Центральное композиционное планирование – это поэтапное построение плана, которое
позволяет получить адекватное уравнение за минимальное количество экспериментов.
Первоначально предполагают, что модель процесса линейна, то есть содержит свободный и линейные члены и парные взаимодействия. Такой эксперимент содержит две серии опытов.
Первая серия экспериментов для случая полного факторного эксперимента проводится по плану 2k.
Вторая серия из n0 опытов проводится в центре эксперимента, чтобы найти ошибку воспроизводимости.
Слайд 41
Для определения числа опытов n0, пользуются таблицей:
при k
= 2 n0 = 4,
k = 3 n0 = 6,
k = 4 n0 = 6 и т. д.
Суть идеи проверки адекватности модели в центре эксперимента рассмотрим на однофакторном эксперименте.
Уравнение прямой
yр = a0 + a1 x1
точно проходит через экспериментальные точки y1 и y2 , то есть адекватно в периферийных точках. В центральной точке с координатой x = 0 по уравнению имеем yр0 = a0 . Но значение y0, полученное как среднее по опытам, проведенным в этой точке, равно:
Слайд 42
где Δy = tp*Sx , где tp -
коэффициент Стьюдента (берется по таблице),
Sx – среднеквадратичное отклонение:
y
= a0 + a1 x1 + . . . + ak xk + a12 x1 x2 + a13 x1 x3 + . . . + a k -1 ,k xk-1 xk + a11 x12 + a22 x22 + . . . + akk xk2 .
Если адекватность линейного уравнения не доказана, то необходимо перейти к модели второго порядка:
Для этого проводится третья серия экспериментов, т.е. строится план второго порядка.
Слайд 43
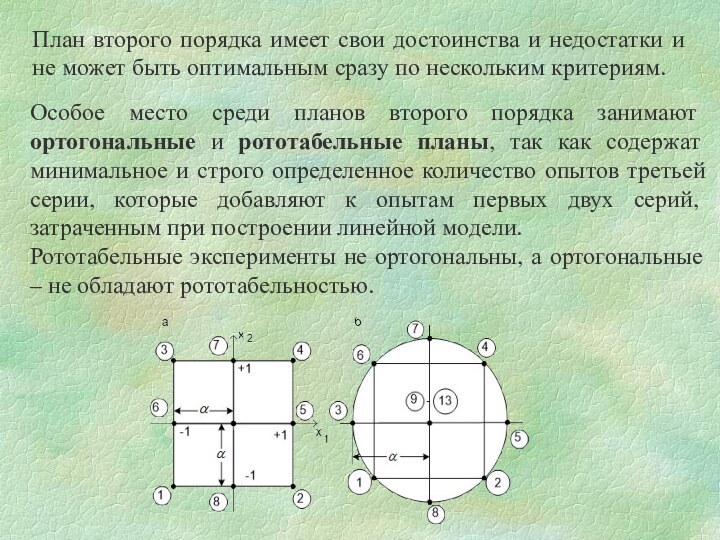
План второго порядка имеет свои достоинства и недостатки
и не может быть оптимальным сразу по нескольким критериям.
Особое место среди планов второго порядка занимают ортогональные и рототабельные планы, так как содержат минимальное и строго определенное количество опытов третьей серии, которые добавляют к опытам первых двух серий, затраченным при построении линейной модели.
Рототабельные эксперименты не ортогональны, а ортогональные – не обладают рототабельностью.
Слайд 44
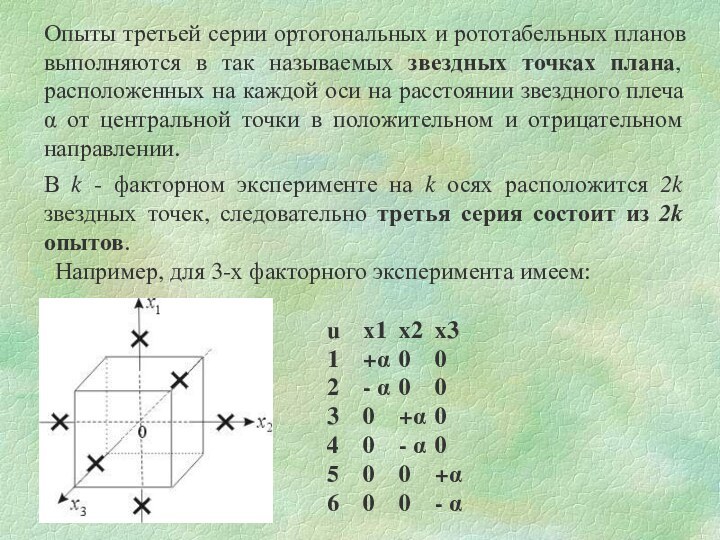
Опыты третьей серии ортогональных и рототабельных планов выполняются
в так называемых звездных точках плана, расположенных на каждой
оси на расстоянии звездного плеча α от центральной точки в положительном и отрицательном направлении.
u х1 x2 x3
1 +α 0 0
2 - α 0 0
3 0 +α 0
4 0 - α 0
5 0 0 +α
6 0 0 - α
В k - факторном эксперименте на k осях расположится 2k звездных точек, следовательно третья серия состоит из 2k опытов.
Например, для 3-х факторного эксперимента имеем:
Слайд 45
План становится ортогональным, если звездное плечо α подобрано
так, что нормальная матрица в методе наименьших квадратов вырождается
в диагональную, следовательно,
при i ≠ j .Это происходит при следующих значениях звездного плеча α :
α = 1,0 при k =2,
α = 1,21 при k = 3 ,
α = 1,41 при k = 4 и т. д.
Для такого эксперимента полученные ранее коэффициенты регрессии при линейных членах и парных взаимодействиях пересчитывать не надо.
Все три серии опытов участвуют в расчете новых коэффициентов a11, a22, . . . , akk и пересчете коэффициента а0.
Слайд 46
Для рототабельного плана второго порядка (для случая полного
факторного эксперимента) звездное плечо вычисляется по формуле:
α =
2k/4 .
Тогда:
α = 1,41 при k =2,
α = 1,68 при k = 3 ,
α = 2,0 при k = 4 и т. д.
После третьей серии опытов по рототабельному плану коэффициенты при линейных членах и парных взаимодействиях также не пересчитываются. Рассчитываются только новые коэффициенты a11, a22, . . . , akk и пересчитывается коэффициент а0.
По этим коэффициентам нормальная матрица не ортогональна, приходится решать систему из (k+1) уравнений с (k+1) неизвестными. Причем при составлении нормальных уравнений должны участвовать опыты всех трех серий.
Слайд 47
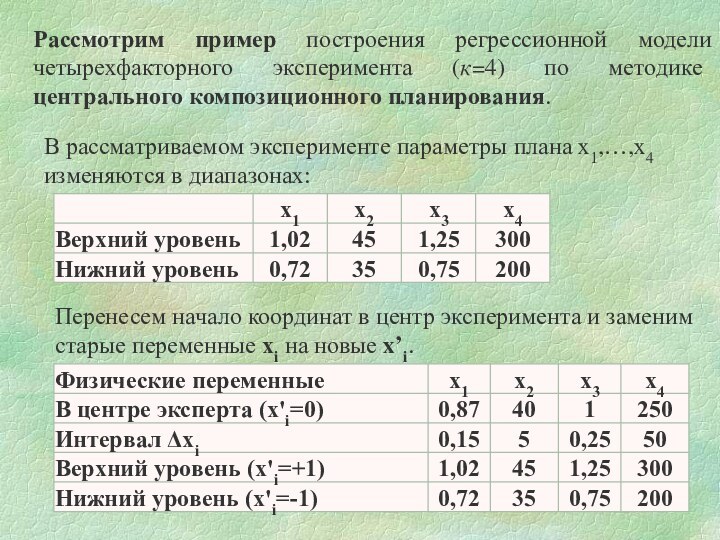
Рассмотрим пример построения регрессионной модели четырехфакторного эксперимента (к=4)
по методике центрального композиционного планирования.
В рассматриваемом эксперименте параметры
плана х1,…,х4 изменяются в диапазонах:
Перенесем начало координат в центр эксперимента и заменим старые переменные хi на новые x’i.
Слайд 48
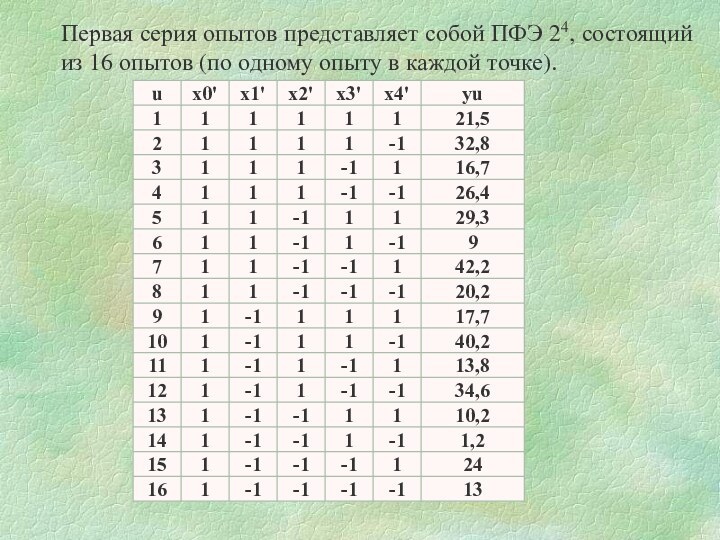
Первая серия опытов представляет собой ПФЭ 24, состоящий
из 16 опытов (по одному опыту в каждой точке).
Слайд 49
Подсчитаем коэффициенты регрессии аi, принимая во внимание только
парные взаимодействия:
Слайд 50
В результате такого эксперимента получаем регрессию:
yp =
22,05 + 2,71 x1 + 3,41 x2 – 1,81
x3 – 0,12 x4 – 3,83 x1 x2 +
+0,2 x1 x3 + 2,79 x1 x4 + 4,4 x2 x3 – 7,91 x2 x4 – 0,4 x3 x4 .
Имеем 11 членов уравнения при 16 опытах, следовательно, отброшено 5 членов: четыре тройных и одно четверное взаимодействия. Они “по определению“ незначимы, но в этом можно убедиться, подсчитав сумму квадратов, принадлежащую этим членам:
= (21,52+ 32,82+...+132) –16 (22,052 + 2,712 +...+ 0,42 ) =0,63
При 5 степенях свободы вклад всех отброшенных членов в общую дисперсию очень мал, однако для его оценки по критерию Фишера необходимо иметь ошибку воспроизводимости эксперимента.
Слайд 51
Для этого проводим вторую серию из n0 =
6 опытов в центре. План этой части эксперимента приведен
в таблице:
Вычислим суммы, среднее и доверительный интервал:
12,5 + . . . + 13,0 = 74,9;
y0 cp = y0 = 74,9 / 6 = 12,48 ;
Слайд 52
(12,52+...+13,02) -74,92/6 = 1,9;
Критерий Фишера для отброшенных
членов:
Это меньше табличного значения FT(0,95; 5; 5) =
5,1, поэтому все отброшенные члены не значимы.
Слайд 53
Полезно провести оценку значимости членов полученной регрессии. Мало
значимыми могут быть члены с наименьшими значениями коэффициентов регрессии,
например, а4х4, а13х1х3 и а14х1х4.
Проверим их по критерию Фишера, рассчитав сумму квадратов отклонений по формуле:
SSai = ai2 N.
При табличном значении FT(0,95; 1; 5) = 6,6 для указанных членов регрессии критерии Фишера будут следующими:
т.е. только член с коэффициентом a14 находится на пределе значимости, и его можно оставить в уравнении.
Слайд 54
В центре эксперимента значение по уравнению yp0 не
совпадает с экспериментальным значением y0 = 12,48 ± 0,65
, то есть модель в этой точке не адекватна.
Необходимо добавить 2k = 8 опытов в звездных точках и до- строить модель до квадратичной.
Переходим к третьей серии экспериментов.
Звездное плечо α = 24/4 = 2. Координаты звездных точек указаны в таблице:
Слайд 55
Экспериментальные данные (третья серия экспериментов) в звездных точках
приведены в таблице:
Слайд 56
Полный план для расчета по третьей серии содержит
25 экспериментов:
Первые 16 строк – первая серия экспериментов
Вторая серия
Третья
серия
Слайд 57
Нормальная система уравнений для третьей серии будет иметь
вид:
Слайд 58
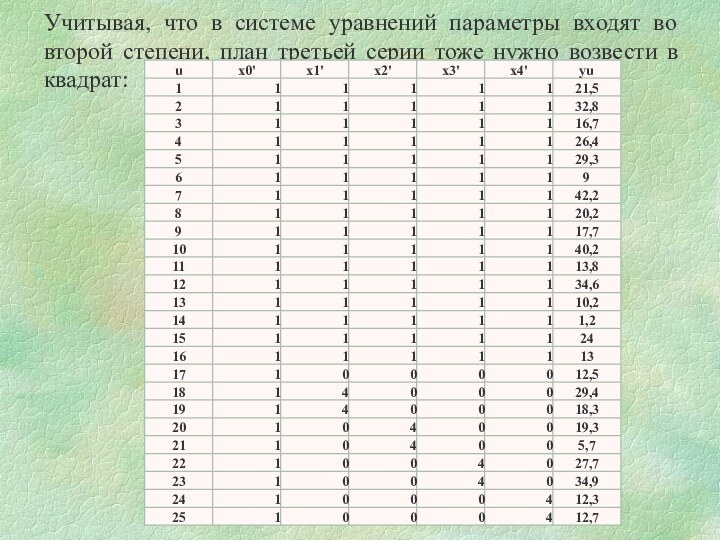
Учитывая, что в системе уравнений параметры входят во
второй степени, план третьей серии тоже нужно возвести в
квадрат:
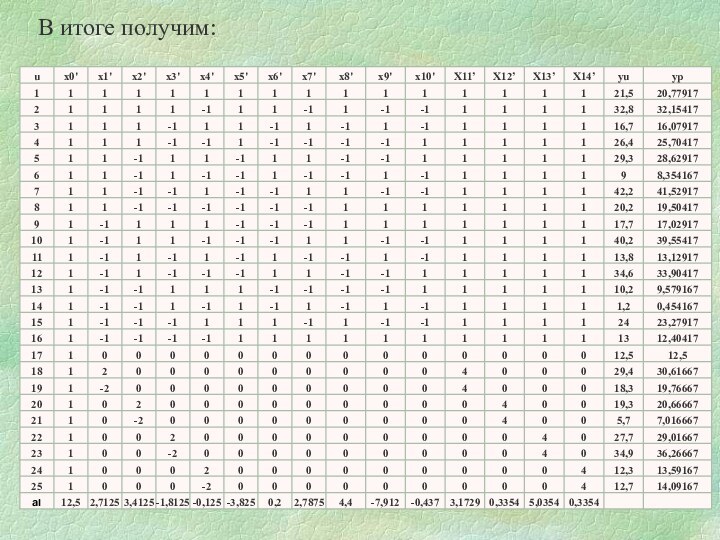
Слайд 59
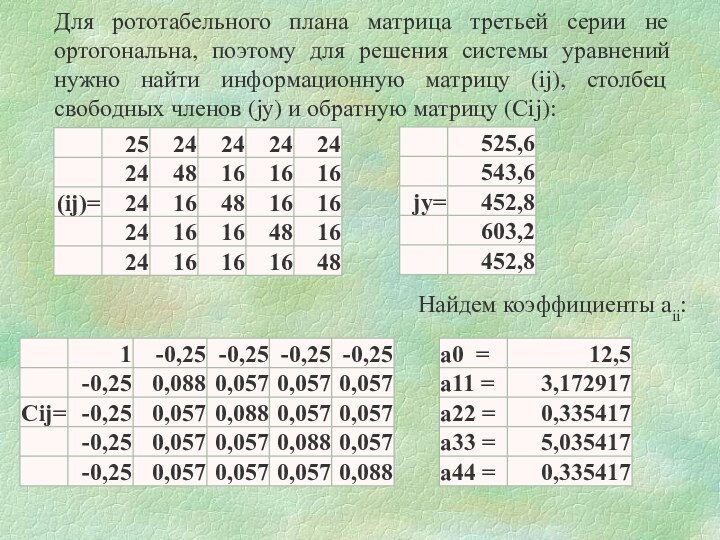
Для рототабельного плана матрица третьей серии не ортогональна,
поэтому для решения системы уравнений нужно найти информационную матрицу
(ij), столбец свободных членов (jy) и обратную матрицу (Сij):
Найдем коэффициенты aii:
Слайд 61
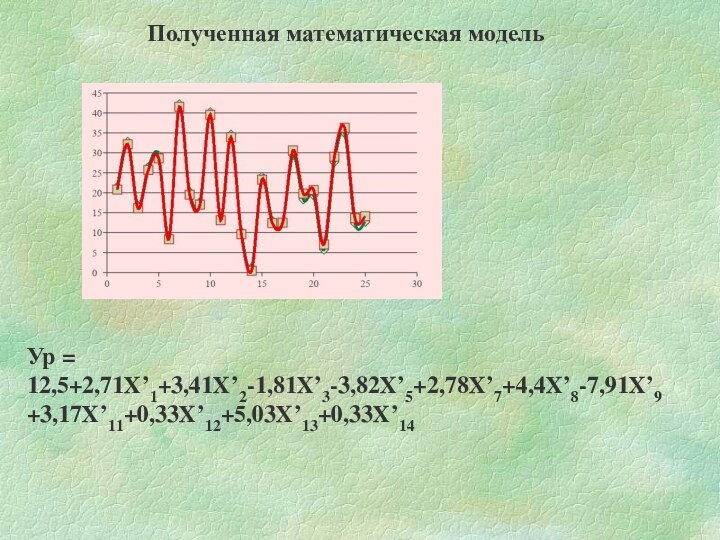
Графическое представление полученной математической модели
Слайд 62
Дисперсионный анализ полученной модели
Подсчитаем суммы квадратов:
= 22,72+32,12+162+…+14,12 =
13868
= 13845,6
= 22,4
Слайд 63
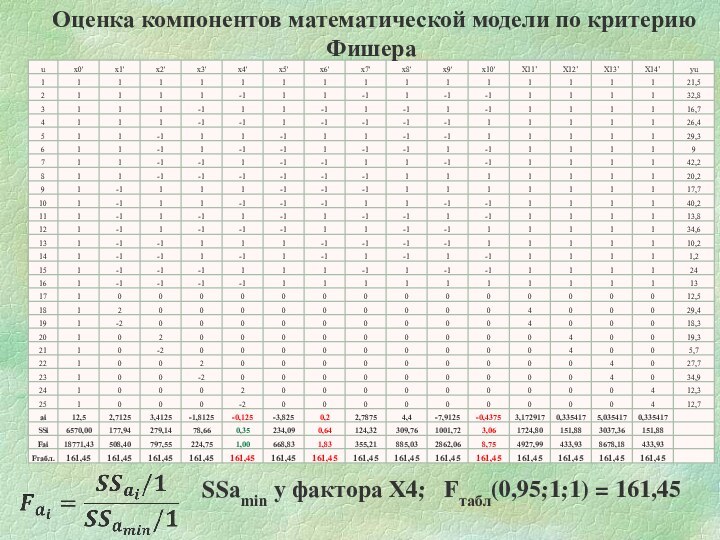
Оценка компонентов математической модели по критерию Фишера
SSаmin у
фактора Х4; Fтабл(0,95;1;1) = 161,45