- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Содержание
- 2. Чертеж – международный язык общения техников. Начертательная
- 3. Базовые геометрические элементы начертательной геометрии
- 4. Точка – абстрактное математическое понятие. Нульмерный объект
- 5. Проективное пространство
- 6. Для устранения неоднородности Евклидова пространства
- 7. Метод проецирования
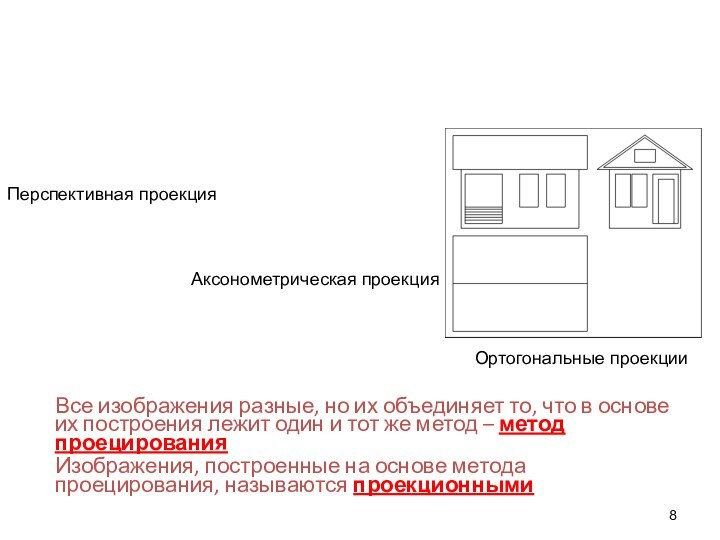
- 8. Все изображения разные, но их объединяет то,
- 9. Пк – плоскость проекцийS – центр проецированияА
- 10. Для любой точки пространства SA ∩ Пк
- 11. Варианты метода проецирования
- 12. Центральное проецирование (коническое)Расстояние от S до плоскости
- 13. Параллельное проецирование (цилиндрическое)S (центр проецирования) –
- 14. Параллельное проецирование
- 16. Проекции Ак соответствует любая точка на проецирующей
- 17. Введем дополнительные условия:Рассматриваем только прямоу-гольное проецирование.Вводим пространственную
- 18. Ортогонально спроецируем точку А совместно с ортогональной
- 19. В этом случае на полученных
- 20. Ортогональные проекции точки на две
- 21. Метод Монжа
- 22. Ортогональная система двух плоскостей проекций
- 23. П1 П2П1
- 24. Плоскости проекций П1 и П2 совмещены в одну общую плоскость.
- 25. Проецирование точки
- 26. Точка в I-ой четвертиНаглядное изображениеПлоскостное изображение - Эпюр
- 27. Горизонтальная и фронтальная проекции точки
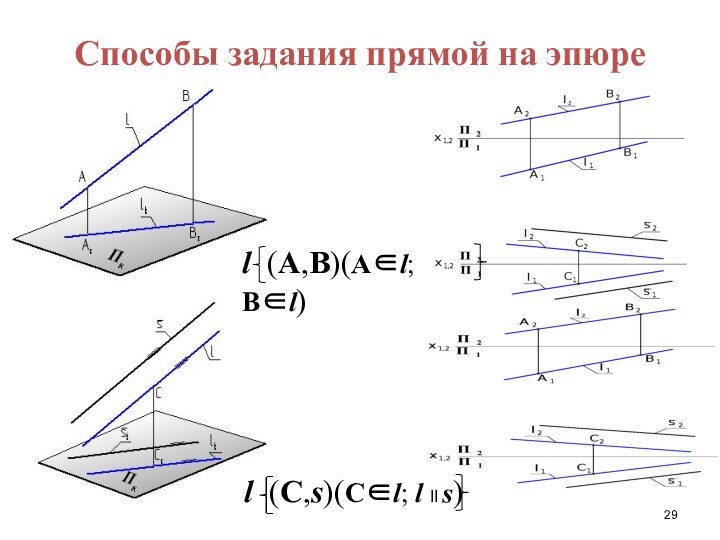
- 28. Проецирование прямой линии
- 29. Способы задания прямой на эпюреl (A,B)(Al; Bl) l (С,s)(Cl; l ll s)
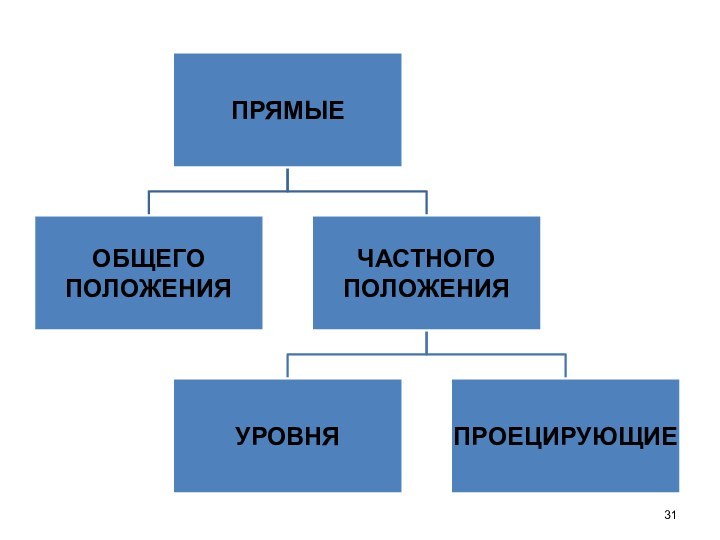
- 30. Положение прямой относительно плоскости проекцийПрямая общего
- 32. l II П1 и l II П2l
- 33. Характерная особенность эпюра прямой общего положения –
- 34. Прямая уровняЭто прямая параллельная какой-либо одной плоскости проекцийl II Пк
- 35. Горизонталь – h Это прямая параллельная горизонтальной
- 36. Фронталь – f Это прямая параллельная фронтальной
- 37. Характерная особенность эпюра горизонтали и фронтали –
- 38. Профильная прямая - pЭто прямая параллельная профильной плоскости проекций П3
- 39. Горизонтально-проецирующая прямая Это прямая перпендикулярная горизонтальной плоскости
- 40. Фронтально-проецирующая прямая Это прямая перпендикулярная фронтальной плоскости
- 41. Характерная особенность эпюра проецирующей прямой – одна из проекций прямой точка
- 42. Взаимное положение двух прямых
- 43. Пересекающиеся прямыеm ∩ n = D
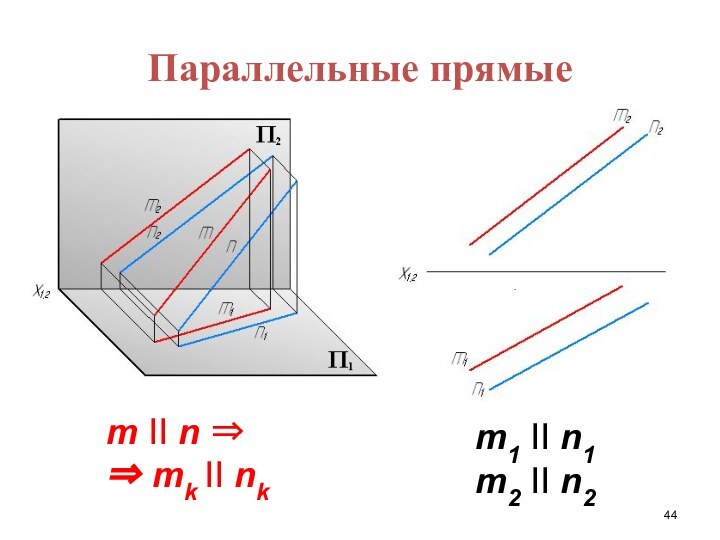
- 44. Параллельные прямыеm II n mk II nkm1 II n1m2 II n2
- 45. Скрещивающиеся прямыеm n m II
- 46. Плоскость
- 47. Плоскость - это один из видов поверхности (плоская поверхность).
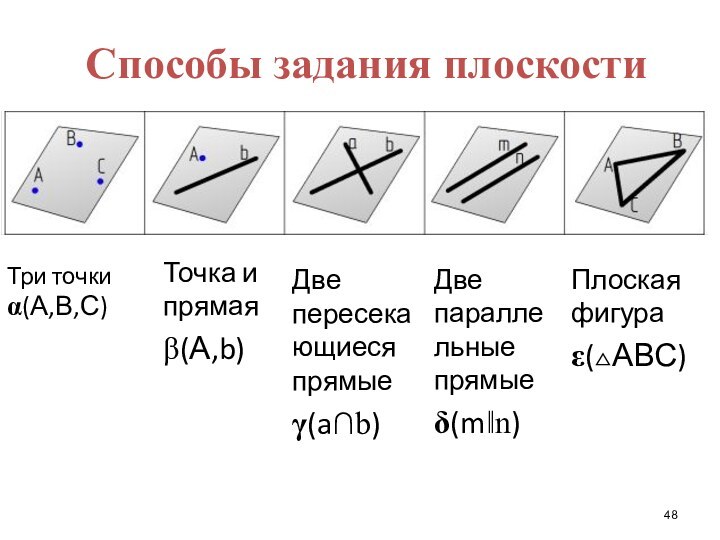
- 48. Три точкиα(А,В,С)Способы задания плоскостиДве параллельные прямыеδ(m‖n)Точка и прямаяβ(А,b)Плоская фигураε(АВС)Две пересекающиеся прямыеγ(a∩b)
- 49. Положение плоскости относительно плоскостей проекций
- 50. α II Пк α ПкОбщее положениеЧастное положениеβ Пкγ II Пк Проецирующая плоскостьПлоскость уровня
- 51. Плоскость общего положенияПлоскость непараллельная и неперпендикулярная плоскостям
- 52. Плоскости частного положения
- 53. Это плоскости перпендикулярные одной из плоскостей проекцийГоризонтально-проецирующаяФронтально-проецирующаяТ1
- 54. Это плоскости параллельные одной из плоскостей проекцийГоризонтальная
- 55. У плоскости частного положения одна из проекций обязательно имеет форму прямой линии. Вывод:
- 56. Прямая линия в плоскости
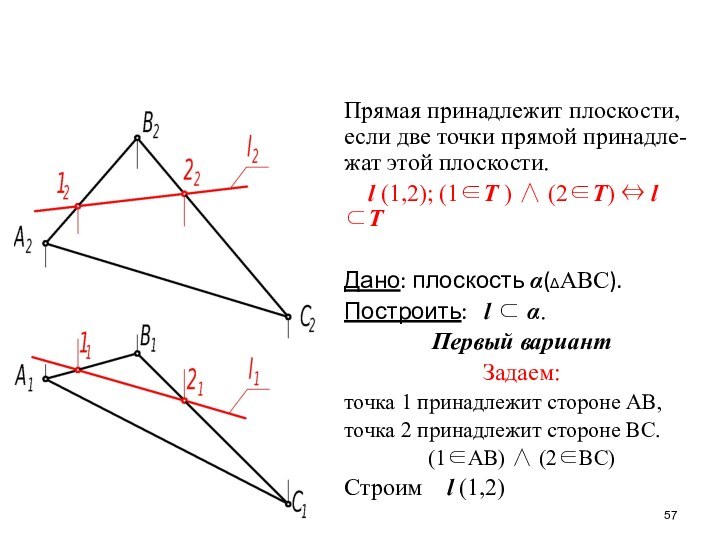
- 57. Прямая принадлежит плоскости, если две точки прямой
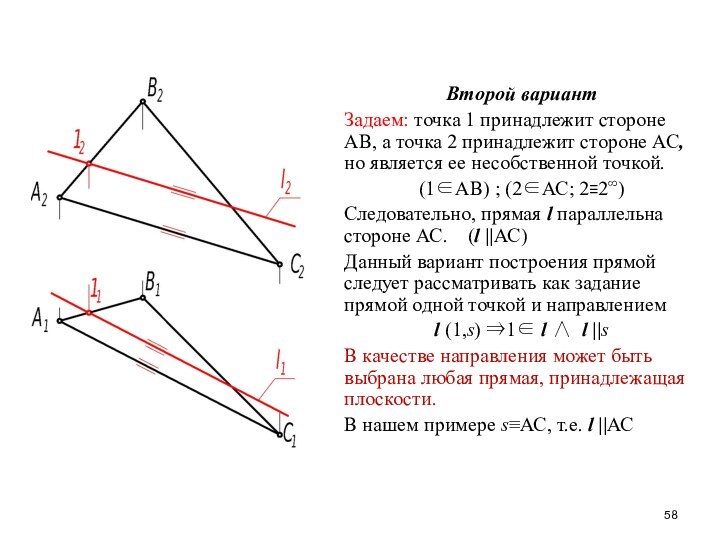
- 58. Второй вариантЗадаем: точка 1 принадлежит стороне АВ,
- 59. Прямые уровня плоскости
- 60. Горизонталь плоскостиДано: Плоскость αАВСПостроить: h αЗадаем
- 61. Фронталь плоскостиДано: Плоскость αАВСПостроить: f αЗадаем
- 62. ТОЧКА В ПЛОСКОСТИ
- 63. Точка принадлежит плоскости, если она
- 64. Скачать презентацию
- 65. Похожие презентации


















































Слайд 2
Чертеж – международный язык общения техников.
Начертательная геометрия
– грамматика этого языка (чертежа).
изображений пространственных объектов на плоскости, а также способы преобразования полученных изображений для упрощения решения различных инженерных задач.Слайд 4 Точка – абстрактное математическое понятие. Нульмерный объект (не
имеет измерений).
Линия – непрерывное одномерное множество точек ( цепочка
точек). Измерение : только длина. Толщины нет.Поверхность – непрерывное двумерное множество точек. Измерения : длина, ширина, площадь. Толщины и объема нет.
Слайд 6
Для устранения неоднородности Евклидова пространства
(m n) (m ∩ n = F
)условно принято,
что параллельные между собой прямые
пересекаются
в бесконечно удаленной точке F -
несобственной точке пространства.
Евклидово пространство, дополненное несобственными элементами, называют проективным.
Слайд 8 Все изображения разные, но их объединяет то, что
в основе их построения лежит один и тот же
метод – метод проецированияИзображения, построенные на основе метода проецирования, называются проекционными
Перспективная проекция
Аксонометрическая проекция
Ортогональные проекции
Слайд 9
Пк – плоскость проекций
S – центр проецирования
А –
объект (точка)
SA – проецирующая
прямаяМетод проецирования
SA ∩ ПК = АК
АК – проекция объекта (точки) А на плоскости проекций Пк
Слайд 12
Центральное проецирование
(коническое)
Расстояние от S до плоскости проекций Пк
измеримая величина.
S (центр проецирования) -–
реальная точка. SA ∩ SB ∩ SC …= S
Слайд 13
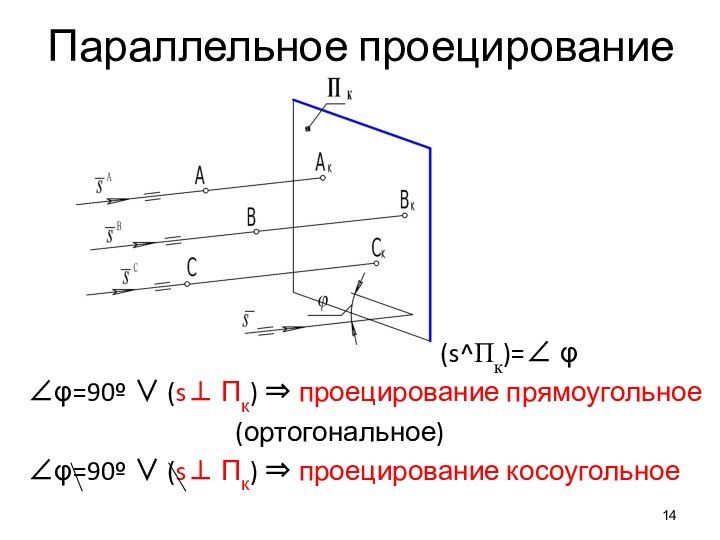
Параллельное проецирование
(цилиндрическое)
S (центр проецирования) –
несобственная точка.
S S
SA ∩ SB ∩ SC …= S
следовательно
S A S B S C …
s – направление проецирования; S s
s
Слайд 14
Параллельное проецирование
(s^Пк)= φ
φ=90º (s Пк) проецирование прямоугольное
(ортогональное)
φ=90º (s Пк) проецирование косоугольное
Слайд 16 Проекции Ак соответствует любая точка на проецирующей прямой,
проходящей через точку А.
Одна проекция точки без каких-либо
дополнительных условий однозначно не определяет ее положение в пространстве.
Слайд 17
Введем дополнительные условия:
Рассматриваем только прямоу-гольное проецирование.
Вводим пространственную систему
координат Oxyz, и задаем положение точки, например, А в
этой системе.Заменяем обозначение плоско-сти проекций Пк на П1 и вводим вторую плоскость проекций П2, перпендикулярную П1 (П1 П2).
Ориентируем пространствен-ную систему координат так, чтобы две координатные плоскости Oxy и Oxz расположились параллельно плоскостям проекций П1 и П2 соответственно (Oxy ‖ П1; Oxz ‖ П2).
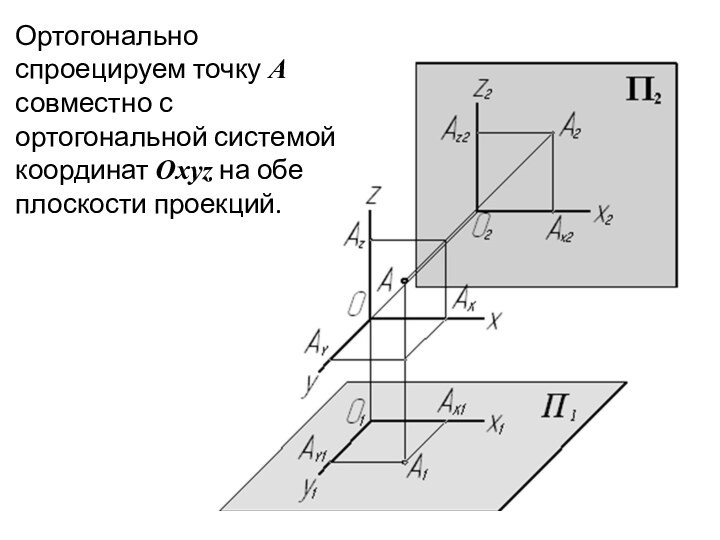
Слайд 18 Ортогонально спроецируем точку А совместно с ортогональной системой
координат Oxyz на обе плоскости проекций.
Слайд 19 В этом случае на полученных проекциях
мы имеем все три координаты точки А относительно выбранной
системы координат, которые отображаются в истинную величину.Следовательно:
Слайд 20 Ортогональные проекции точки на две взаимно
перпендикулярные плоскости однозначно определяют положение точки в пространстве и
делают изображения обратимыми.
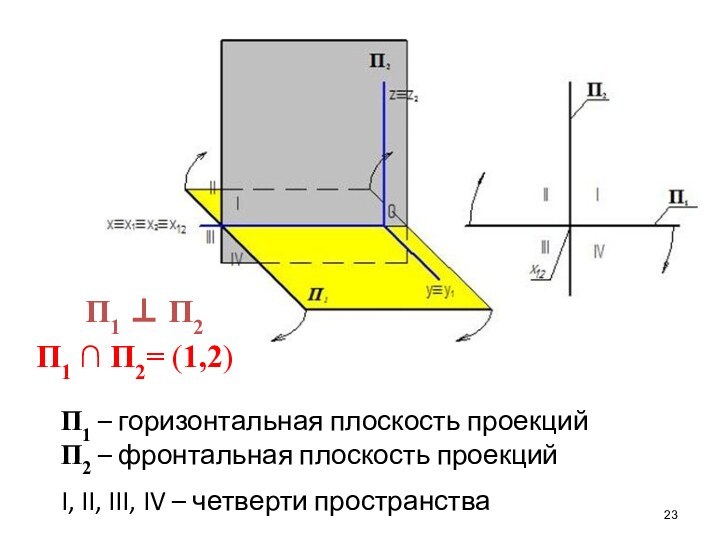
Слайд 23
П1 П2
П1 ∩
П2= (1,2)
П1 – горизонтальная плоскость проекций
П2 – фронтальная плоскость
проекцийI, II, III, IV – четверти пространства
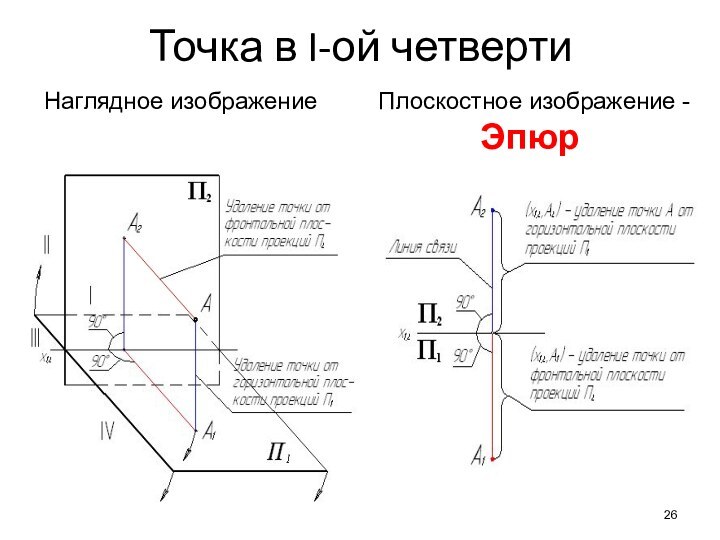
Слайд 27 Горизонтальная и фронтальная проекции точки располагаются
на одной прямой, перпендикулярной оси x12
А1А2 х12Расстояние от оси x12 до горизонтальной проекции точки определяет расстояние от самой точки до фронтальной плоскости проекций.
(х12 , А1) = (А, П2) - глубина
Расстояние от оси x12 до фронтальной проекции точки определяет расстояние от самой точки до горизонтальной плоскости проекций.
(х12 , А2) = (А, П1) - высота
Слайд 30
Положение прямой относительно
плоскости проекций
Прямая
общего положения
Прямые частного
положения
l II Пk и l Пk
l II
Пk l Пk
Прямая уровня
Проецирующая
прямая
Слайд 32
l II П1 и l II П2
l
П1 и l П2
l1 II x1,2 и l2
II x1,2l1 x1,2 и l2 x1,2
Прямая общего положения
Это прямая не параллельная и не перпендикулярная
ни одной из плоскостей проекций
Слайд 33 Характерная особенность эпюра прямой общего положения – горизонтальная
и фронтальная проекции прямой не параллельны и не перпендикулярны
координатной оси х12
Слайд 35
Горизонталь – h
Это прямая параллельная горизонтальной плоскости проекций
h II П1
AB h
AB II П1 h(AB)^П2
h2 II x1,2
А1В1 IABI
h1(А1В1) ^ x1,2
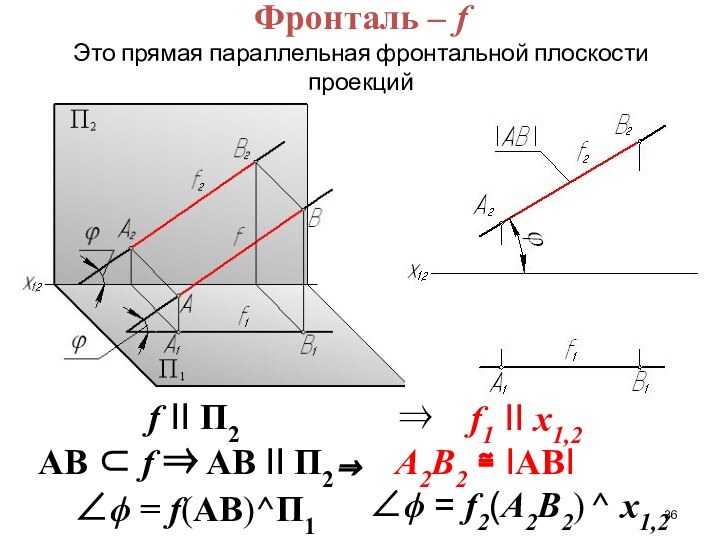
Слайд 36
Фронталь – f
Это прямая параллельная фронтальной плоскости проекций
f II П2
AB f
AB II П2 f(AB)^П1
f1 II x1,2
А2В2 IABI
f2(А2В2) ^ x1,2
Слайд 37 Характерная особенность эпюра горизонтали и фронтали – одна
из проекций параллельна координатной
оси х1,2
Слайд 39
Горизонтально-проецирующая прямая
Это прямая перпендикулярная горизонтальной плоскости проекций
m
П1 m II П2
AB m AB
II П2 m1 – точка m2 x1,2
А1В1 - точка А2В2 IABI
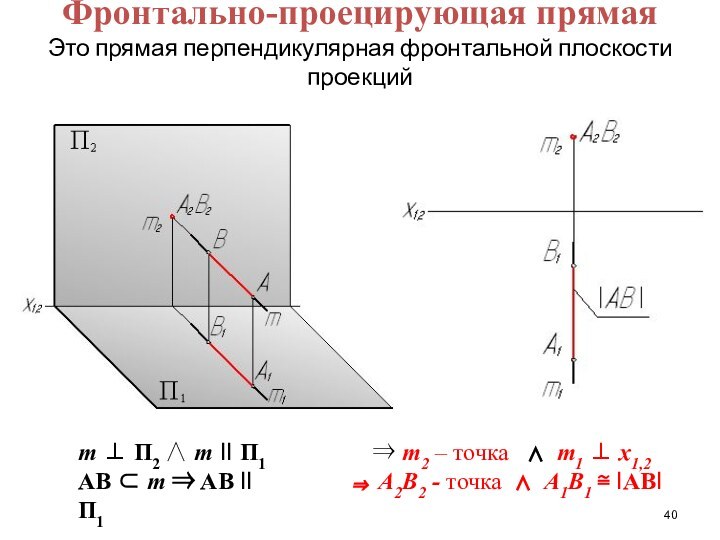
Слайд 40
Фронтально-проецирующая прямая
Это прямая перпендикулярная фронтальной плоскости проекций
m
П2 m II П1
AB m AB
II П1 m2 – точка m1 x1,2
А2В2 - точка А1В1 IABI
Слайд 48
Три точки
α(А,В,С)
Способы задания плоскости
Две параллельные прямые
δ(m‖n)
Точка и прямая
β(А,b)
Плоская
фигура
ε(АВС)
Две пересекающиеся прямые
γ(a∩b)
Слайд 50
α II Пк α Пк
Общее положение
Частное
положение
β Пк
γ II Пк
Проецирующая плоскость
Плоскость уровня
Слайд 51
Плоскость общего положения
Плоскость непараллельная и неперпендикулярная плоскостям проекций
Вывод:
Ни одна из проекций плоскости не имеет форму прямой
линии
Слайд 53
Это плоскости перпендикулярные одной из плоскостей проекций
Горизонтально-проецирующая
Фронтально-проецирующая
Т1 –
прямая и Т1≡ ТП1
Т2 – прямая и Т2≡ ТП2
Проецирующие
плоскостиТ П1
Т П2
Слайд 54
Это плоскости параллельные одной из плоскостей проекций
Горизонтальная плоскость
Фронтальная
плоскость
Плоскости уровня
α II П1
β II П2
α 2 – прямая
и α 2≡ α П2и α 2II x1,2
β 1 – прямая и β 1≡ β П1
и β 1 II x1,2
АВС α АВС II П1А1В1С1 АВС
АВС β АВС II П2А2В2С2 АВС
Слайд 55 У плоскости частного положения одна из проекций обязательно
имеет форму прямой линии.
Вывод:
Слайд 57 Прямая принадлежит плоскости, если две точки прямой принадле-жат
этой плоскости.
l (1,2); (1Т ) (2Т)
l Т Дано: плоскость αАВС.
Построить: l α.
Первый вариант
Задаем:
точка 1 принадлежит стороне АВ,
точка 2 принадлежит стороне ВС.
(1АВ) (2ВС)
Строим l (1,2)
Слайд 58
Второй вариант
Задаем: точка 1 принадлежит стороне АВ, а
точка 2 принадлежит стороне АС, но является ее несобственной
точкой.(1АВ) ; (2АС; 2≡2∞)
Следовательно, прямая l параллельна стороне АС. (l ||АС)
Данный вариант построения прямой следует рассматривать как задание прямой одной точкой и направлением
l (1,s) 1 l l ||s
В качестве направления может быть выбрана любая прямая, принадлежащая плоскости.
В нашем примере sАС, т.е. l ||АС
Слайд 60
Горизонталь плоскости
Дано: Плоскость αАВС
Построить: h α
Задаем h
(А,1); 1ВС
h 1 h2 x1,2
Это прямая,
принадлежащая плоскости,и параллельная горизонтальной плоскости
проекций
Слайд 61
Фронталь плоскости
Дано: Плоскость αАВС
Построить: f α
Задаем f
(А,1); 1ВС
f 2 f1 x1,2
Это прямая,
принадлежащая плоскости,и параллельная фронтальной плоскости
проекций