Слайд 2
Sonic Log
The sonic log is a porosity log
that measures interval transit time (Δt) of a compressional
sound wave traveling through one foot of formation.
Interval transit time (Δt) in microseconds per foot is the reciprocal of the velocity of a compressional sound wave in feet per second.
Слайд 3
Sonic Log (Cont.)
The sonic log device consists of
one or more sound transmitters, and two or more
receivers.
Modern sonic logs are borehole compensated devices (BHC). These devices greatly reduce the spurious effects (假性效應) of borehole size variations (Kobesh and Blizard, 1959), as well as errors due to tilt (傾斜) of the sonic tool (Schlumberger, 1972).
Слайд 4
Sonic Log
聲波井測為量測聲波(通常為壓縮聲波)通過 1英呎厚的地層所需的間隔傳遞時間。
利用聲波井測所記錄的間隔傳遞時間、配合已知(或假設)的地層岩基以及地層流體的間隔傳遞時間,可估算出地層孔隙率 (聲波孔隙率)。
Слайд 6
Sonic Log (Cont.)
Interval transit time (Δt) is record
in tracks #2 and #3 (in your example Figure).
A sonic derived porosity curve is sometimes recorded in tracks #2 and #3, along with the Δt curve.
Track #1 normally contains a caliper log and a gamma ray log or an SP log.
Слайд 8
Sonic Log (Cont.)
The interval transit time (Δt) is
dependent upon both lithology and porosity.
Therefore, a formation's
matrix velocity (Table 1) must be known to derive sonic porosity either by chart (Fig. 27) or by formula (Wyllie et al, 1958).
Слайд 9
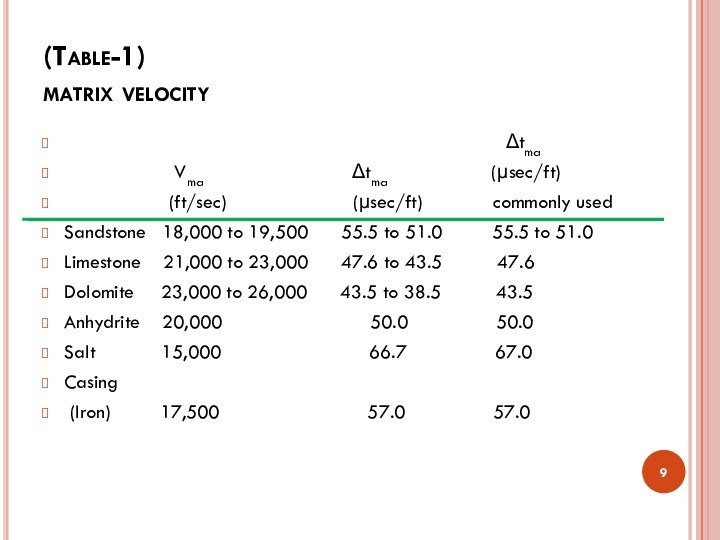
(Table-1)
matrix velocity
Δtma
Vma Δtma (μsec/ft)
(ft/sec) (μsec/ft) commonly used
Sandstone 18,000 to 19,500 55.5 to 51.0 55.5 to 51.0
Limestone 21,000 to 23,000 47.6 to 43.5 47.6
Dolomite 23,000 to 26,000 43.5 to 38.5 43.5
Anhydrite 20,000 50.0 50.0
Salt 15,000 66.7 67.0
Casing
(Iron) 17,500 57.0 57.0
Слайд 10
(1) derive sonic porosity by chart
Слайд 12
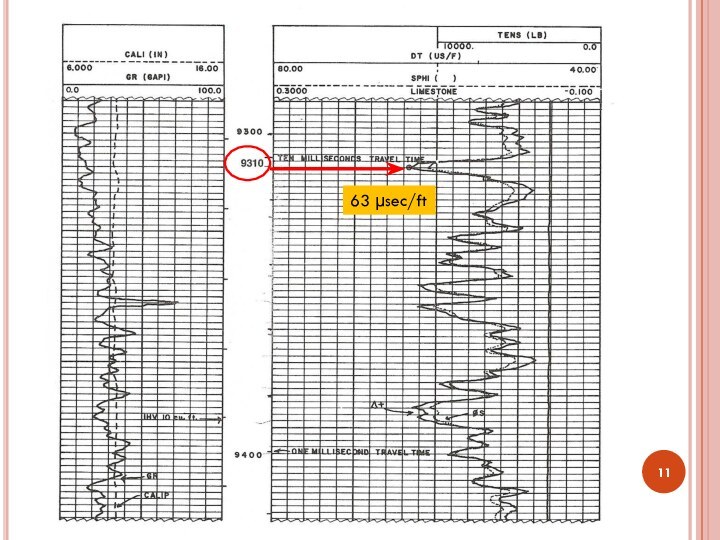
Given:
Vma=26000 ft/sec (Dolomite)
Δt=63 μsec/ft @ 9310 ft
Note:
The
formation's matrix velocity must be known
Derive sonic porosity by
chart
Слайд 13
Exercise – find sonic porosity by chart
(1)
Depth =
9310 ft
Lithology [=] Dolomite (Vma=26000 ft/sec)
Sonic porosity =
?
(2)
Depth = 9320 ft
Lithology [=] Limestone (Vma=21000 ft/sec)
Sonic porosity = ?
Слайд 14
(2) derive sonic porosity by formula
Слайд 15
Derive sonic porosity by Wyllie formula
Where:
Фsonic
= sonic derived porosity
Δtma = interval transit time
of the matrix
Δtlog = interval transit time of formation
Δtf = interval transit time of the fluid in the well bore
(fresh mud = 189;salt mud = 185)
Слайд 16
Exercise – find sonic porosity by formula
(1)
Depth =
9310 ft
Lithology [=] Dolomite
Mud [=] fresh mud
Sonic porosity
= ?
(2)
Depth = 9320 ft
Lithology [=] Limestone
Mud [=] fresh mud
Sonic porosity = ?
Слайд 17
Sonic porosity for unconsolidated sands
Слайд 18
Sonic porosity for unconsolidated sands
The Wyllie et
al. (1958) formula for calculating sonic porosity can be
used to determine porosity in consolidated sandstones and carbonates.
Where a sonic log is used to determine porosity in unconsolidated sands, an empirical compaction factor or Cp should be added to the Wyllie et al. (1958) equation:
Where Cp = compaction factor
Слайд 19
Sonic porosity for unconsolidated sands (Cont.)
For unconsolidated sands,
The
compaction factor is obtained from:
Where Cp = compaction factor
Δtsh = interval transit time for adjacent shale
C = a constant which is normally 1.0 (Hilchie,1978)
Слайд 20
empirical corrections for hydrocarbon effect
Слайд 21
empirical corrections for hydrocarbon effect
The interval transit tie
(Δt) of a formation is increased due to the
presence of hydrocarbons (i.e. hydrocarbon effect).
If the effect of hydrocarbons is not corrected, the sonic derived porosity will be too high.
Hilchie (1978) suggests the following empirical corrections for hydrocarbon effect:
Ф = Фsonic × 0.7 (gas)
Ф = Фsonic × 0.9 (oil)
Слайд 23
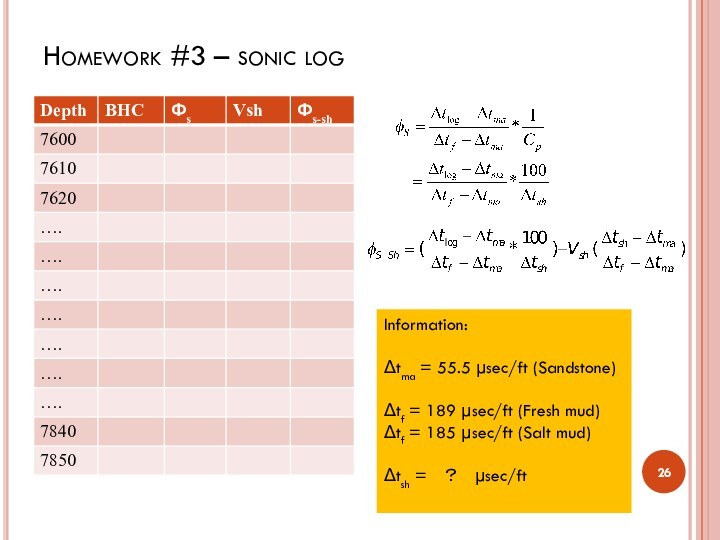
Sonic porosity for shaly sands
After the volume of
shale (Vsh) is determined, it can be used to
correct the porosity log for shale effect. The formula for correcting the sonic log for volume of shale is (Dresser Atlas, 1979):
Where Δtsh = interval transit time for adjacent shale









![Basic well logging analysis – sonic log Exercise – find sonic porosity by chart(1)Depth = 9310 ftLithology [=] Dolomite](/img/tmb/13/1267525/f38739926a72caaa5bef2c4d0d48fd75-720x.jpg)


![Basic well logging analysis – sonic log Exercise – find sonic porosity by formula(1)Depth = 9310 ftLithology [=] Dolomite](/img/tmb/13/1267525/84b0d85c9a3e72f81fb7b446e0d45fd9-720x.jpg)