Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Эконометрика

Содержание

Лабораторная работа № 1Основные описательные статистикиС помощью генератора случайных чисел для дискретной случайной величины X создать выборку объема N=30.Открыть меню «Анализ данных» на вкладке «Данные». (Если его нет, то установить: Файл\Параметры\Надстройки; выбрать Пакет анализа и нажать
Эконометрика/Лабораторные работы в Microsoft Excel/ Лабораторная работа № 1Основные описательные статистикиС помощью генератора случайных чисел для дискретной Для полученной выборки x1, ... , xN объема N =30 вычислить Оценку Среднее отклонение (функция СРОТКЛ())Относительное отклонение по модулю (линейный коэффициент вариации)Мера точностиВероятное отклонениеМера изменчивости (коэффициент вариации) Вычислить параметры распределения с помощью Анализ данных\Описательная статистика и сравнить с рассчитанными по формулам Пример таблицы с вычисленными описательными статистикамиМода (функция МОДА.ОДН())Медиана (функция МЕДИАНА()) =Пример таблицы, Построить гистограмму с помощью Анализ данных\Гистограмма Пример гистограммы, построенной с помощью Анализ данных\Гистограмма (интервал Карманов выбирался автоматически)Вычислить моду Лабораторная работа № 2Группировка данныхСгруппировать полученные в лабораторной работе № 1 значения Вычислить Абсолютные частоты ni (функция ЧАСТОТА. Относится к диапазону ячеек: выделить диапазон Вычислить Среднее значение (для сгруппированных данных)ДисперсиюСреднее квадратичное отклонение sxПостроить интегральную и дифференциальную Пример таблицыПостроить гистограмму с помощью Анализ данных\Гистограмма интервал карманов Построить гистограммыАбсолютных и относительных частотКумулятивных и относительных кумулятивных частот Построить гистограммыЭмпирический дифференциальный и интегральный законы распределенияИнтегральную и дифференциальную функции для нормального закона распределения Вычислить Основные описательные статистики (лабораторная работа №1)При доверительной вероятности γ = 0.95 Лабораторная работа № 4Линейная регрессияДаны две выборки, состоящие из N значений случайных Метод наименьших квадратов Вычислить коэффициенты регрессии Методом наименьших квадратов, решив систему линейных уравнений (*)С помощью Выполнение работыВвести исходные данные на рабочий лист Линейная регрессияДля решения системы ввести Функции рабочего листа НАКЛОН(), ОТРЕЗОК(), ЛИНЕЙН()Выделить два столбца и пять строк, ввести формулу, нажать Ctrl+Shift+Enter Построение диаграммы и линии трендаВыделить два столбца значений X и Y вместе Построение диаграммы и линии тренда Анализ данных \ Регрессия Анализ данных \ РегрессияПроверить, чтобы значения коэффициентов регрессии, найденные разными способами, совпадали! Вычислить коэффициент корреляцииВыборочная ковариация (функция КОВАРИАЦИЯ.В())Коэффициент корреляции (функция КОРРЕЛ(), Анализ данных \ Корреляция) Вычисление коэффициента корреляции Оценить уровень значимости уравнения регрессииКоэффициент детерминацииВ случае одной независимой переменной XF-статистикаm – Сумма квадратов, обусловленная регрессией (RSS)Сумма квадратов, обусловленная ошибкой (ESS)Общая Оценить значимость коэффициентов уравнения регрессииНесмещенная оценка дисперсии остаточной компонентыdjj - диагональные элементы Оценить значимость коэффициента корреляции Найти доверительные интервалы для среднего и дисперсии Лабораторная работа № 5Линейная регрессия для сгруппированных данныхДаны две выборки, состоящие из Выполнение работыВвести исходные данные на рабочий лист Линейная регрессия – сгруппированные данныеДля Выполнение работыСделать проверку Построить уравнение регрессииСделать самостоятельно по аналогии с п. 1 Вычислить коэффициент корреляцииВыборочная ковариацияКоэффициент корреляцииПримечанияПри вычислении средних значений и средних квадратичных отклонений Сумма квадратов, обусловленная регрессией (RSS)Сумма квадратов, обусловленная ошибкой (ESS)Общая Лабораторная работа № 6Множественная линейная регрессияДаны три выборки, состоящие из N значений Выполнение работыВвести исходные данные на рабочий лист Множественная линейная регрессия Для решения Анализ данных \ Регрессия Анализ данных \ Корреляция ВычислитьF.ОБР.ПХ(α = 0,05; k1 = m – 1; k2 = N –
Слайды презентации

Слайд 2 Лабораторная работа № 1
Основные описательные статистики
С помощью генератора

Лабораторная работа № 1Основные описательные статистикиС помощью генератора случайных чисел для

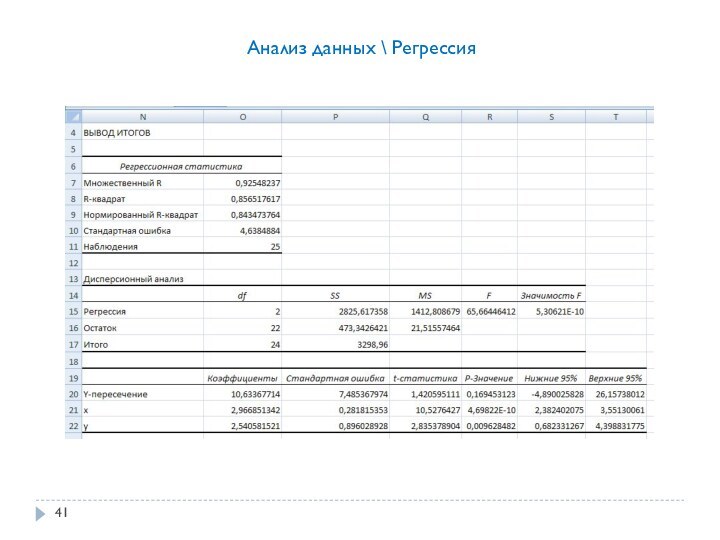
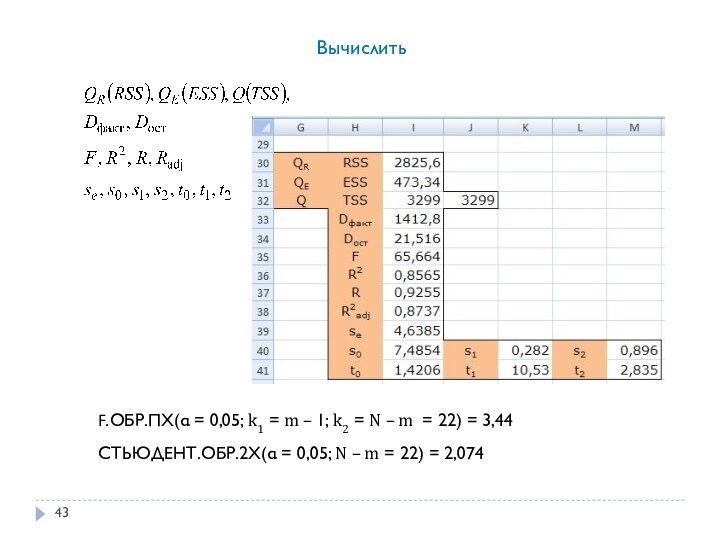
случайных чисел для дискретной случайной величины X создать выборку

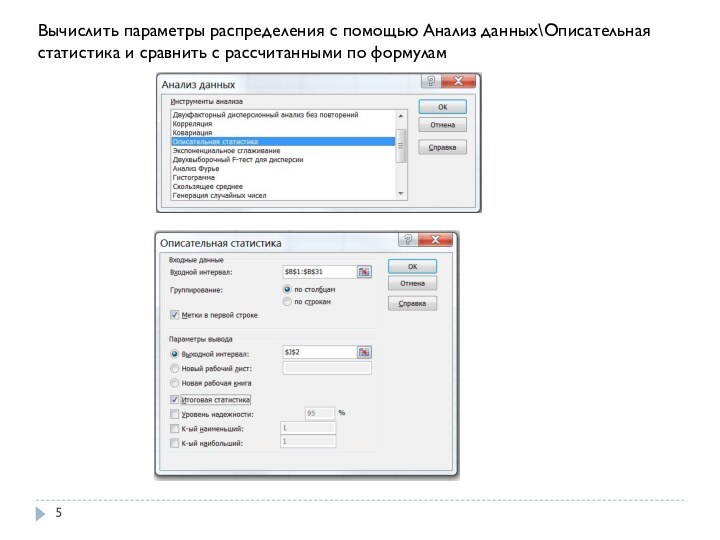
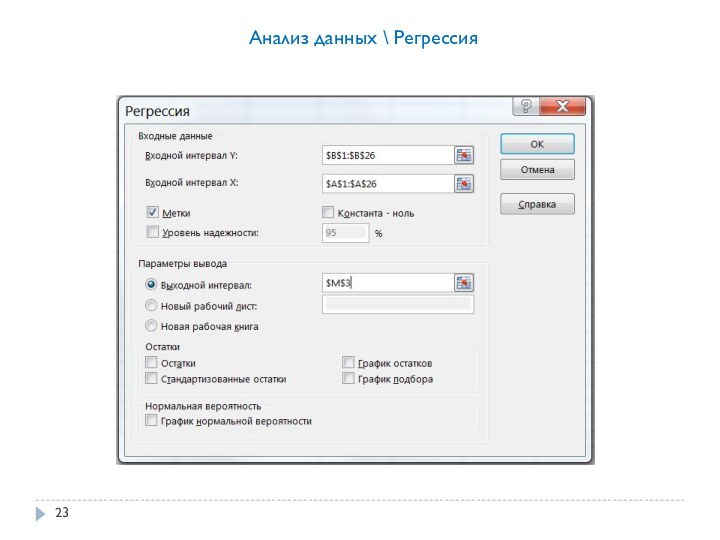
объема N=30.
Открыть меню «Анализ данных» на вкладке «Данные». (Если его нет, то установить: Файл\Параметры\Надстройки; выбрать Пакет анализа и нажать Перейти; поставить флажок Пакет анализа и нажать ОК).
Выбрать Генерация случайных чисел.



В появившемся окне задать параметры нормального распределения: среднее = {Nварианта *10}; стандартное отклонение = {N варианта *2}.
Отсортировать полученные значения в столбце A по возрастанию (вариационный ряд).
Округлить значения (столбец B - функция ОКРУГЛ()). «Число_разрядов» выбрать самостоятельно.

Слайд 3 Для полученной выборки x1, ... , xN объема

Для полученной выборки x1, ... , xN объема N =30 вычислить

N =30 вычислить
Оценку математического ожидания -выборочное среднее

( функция СРЗНАЧ())


Оценку дисперсии (центральный момент второго порядка) - выборочную дисперсию s2, несмещенную оценку дисперсии sx2 (функция ДИСП.В())





Среднее квадратичное отклонение sx (функция СТАНДОТКЛОН.В())
Стандартная ошибка среднего
Выборочный центральный момент 3-го порядка μ3* и несмещенную оценку μ3



Выборочный центральный момент 4-го порядка μ4*


Коэффициент асимметрии (функция СКОС())

Коэффициент эксцесса (функция ЭКСЦЕСС())
Размах выборки

Слайд 4 Среднее отклонение (функция СРОТКЛ())



Относительное отклонение по модулю (линейный

Среднее отклонение (функция СРОТКЛ())Относительное отклонение по модулю (линейный коэффициент вариации)Мера точностиВероятное отклонениеМера изменчивости (коэффициент вариации)

коэффициент вариации)


Мера точности


Вероятное отклонение


Мера изменчивости (коэффициент вариации)



Слайд 5 Вычислить параметры распределения с помощью Анализ данных\Описательная статистика

Вычислить параметры распределения с помощью Анализ данных\Описательная статистика и сравнить с рассчитанными по формулам

и сравнить с рассчитанными по формулам

Слайд 6 Пример таблицы с вычисленными описательными статистиками
Мода (функция МОДА.ОДН())

Медиана

Пример таблицы с вычисленными описательными статистикамиМода (функция МОДА.ОДН())Медиана (функция МЕДИАНА()) =Пример

(функция МЕДИАНА()) =
Пример таблицы, полученной при выполнении «Анализа данных»
Примечание.

Функция МОДА.ОДН() Возвращает наиболее часто встречающееся или повторяющееся значение в массиве или интервале данных.

Слайд 7 Построить гистограмму с помощью Анализ данных\Гистограмма

Построить гистограмму с помощью Анализ данных\Гистограмма

Слайд 8 Пример гистограммы, построенной с помощью Анализ данных\Гистограмма (интервал

Пример гистограммы, построенной с помощью Анализ данных\Гистограмма (интервал Карманов выбирался автоматически)Вычислить

Карманов выбирался автоматически)
Вычислить моду распределения по таблице частот.
1. Определить

модальный интервал (по максимальной частоте). В примере: 43.4-55.6
2. Определить значение моды по формуле

где M0 – значение моды (в примере = 51.16),
x0 – нижняя граница модального интервала (43.4),
h – величина интервала (12.2),
fm – частота модального интервала (12),
fm-1 – частота интервала, предшествующего модальному (5),
fm+1 – частота интервала, следующего за модальным (8).

Слайд 9 Лабораторная работа № 2
Группировка данных
Сгруппировать полученные в лабораторной

Лабораторная работа № 2Группировка данныхСгруппировать полученные в лабораторной работе № 1

работе № 1 значения случайной величины X.

Скопировать столбец

X на новый рабочий лист (Вставить\значения), например, в A2:A31
Выбрать число интервалов группировки. Рассчитать количество интервалов по формулам:
(Стерджесс)
(Брукс и Каррузер)
(Хейнхольд)
(Максимов Ю. Д.)
Рассчитать длину интервала
Округлить h, например, один знак до запятой – до десятых; два – до целых; три или более – кратно 50 или 100
Рассчитать границы и середину интервалов

Слайд 10 Вычислить

Абсолютные частоты ni (функция ЧАСТОТА. Относится к

Вычислить Абсолютные частоты ni (функция ЧАСТОТА. Относится к диапазону ячеек: выделить

диапазону ячеек: выделить диапазон для результата, ввести формулу, нажать

Ctrl+Shift+Enter)
Относительные частоты

и

Накопленные частоты


Накопленные относительные частоты


Выборочную функцию распределения вероятности






Слайд 11 Вычислить

Среднее значение (для сгруппированных данных)


Дисперсию


Среднее квадратичное отклонение

Вычислить Среднее значение (для сгруппированных данных)ДисперсиюСреднее квадратичное отклонение sxПостроить интегральную и

sx

Построить интегральную и дифференциальную функции для нормального закона распределения

с полученными средним значением и дисперсией. Вычислить с помощью функции НОРМ.РАСП(), параметр Интегральная = 0 для дифференциального закона распределения = 1 для интегрального закона распределения
Вычислить дифференциальную функцию распределения по формуле


Примечание. У операции «унарный минус» выше приоритет, чем у ^, поэтому в формуле нужны скобки. Например, EXP(-((H2-$H$11)^2)…

Слайд 12 Пример таблицы
Построить гистограмму с помощью Анализ данных\Гистограмма интервал

Пример таблицыПостроить гистограмму с помощью Анализ данных\Гистограмма интервал карманов – как

карманов – как в функции ЧАСТОТА. (в примере: G2:G6); Установить

флажок Интегральный процент

Слайд 13 Построить гистограммы
Абсолютных и относительных частот








Кумулятивных и относительных кумулятивных

Построить гистограммыАбсолютных и относительных частотКумулятивных и относительных кумулятивных частот

частот

Слайд 14 Построить гистограммы
Эмпирический дифференциальный и интегральный законы распределения

Интегральную и

Построить гистограммыЭмпирический дифференциальный и интегральный законы распределенияИнтегральную и дифференциальную функции для нормального закона распределения

дифференциальную функции для нормального закона распределения

Слайд 15 Вычислить
Основные описательные статистики (лабораторная работа №1)

При доверительной

Вычислить Основные описательные статистики (лабораторная работа №1)При доверительной вероятности γ =

вероятности γ = 0.95 (уровне значимости α = 0.05)

найти

Доверительный интервал для среднего значения
по формуле



tα,N−1 определяется с помощью функции СТЬЮДЕНТ.ОБР.2Х()
с помощью функции ДОВЕРИТ.СТЬЮДЕНТ() – вычисляет
«Анализ данных \Описательная статистика» – поставить флажок Уровень надежности
Доверительный интервал для дисперсии




χα,N−1 определяется с помощью функции ХИ2.ОБР()
Доверительный интервал для среднего квадратичного отклонения

Слайд 16 Лабораторная работа № 4
Линейная регрессия
Даны две выборки, состоящие

Лабораторная работа № 4Линейная регрессияДаны две выборки, состоящие из N значений

из N значений случайных величин X и Y ,

x1, x2, …, xN и y1, y2, …, yN . X − независимая переменная, влияющая на Y. y = (y1, y2, …, yN ) − отклик , x = (x1, x2, …, xN ) − фактор, влияющий на отклик.


Построить уравнение регрессии

Метод наименьших квадратов

Слайд 17 Метод наименьших квадратов

Метод наименьших квадратов

Слайд 18 Вычислить коэффициенты регрессии
Методом наименьших квадратов, решив систему

Вычислить коэффициенты регрессии Методом наименьших квадратов, решив систему линейных уравнений (*)С

линейных уравнений (*)
С помощью функций НАКЛОН(), ОТРЕЗОК()
С помощью функции

ЛИНЕЙН()
Построив линию тренда на диаграмме
С помощью «Анализ данных \ Регрессия»

Слайд 19 Выполнение работы
Ввести исходные данные на рабочий лист Линейная

Выполнение работыВвести исходные данные на рабочий лист Линейная регрессияДля решения системы

регрессия
Для решения системы ввести матрицу коэффициентов и правую часть

системы, найти значения коэффициентов регрессии – решить систему с помощью функций МУМНОЖ(), МОБР()

выделить две ячейки, ввести формулу и нажать Ctrl+Shift+Enter

Слайд 20 Функции рабочего листа НАКЛОН(), ОТРЕЗОК(), ЛИНЕЙН()
Выделить два столбца

Функции рабочего листа НАКЛОН(), ОТРЕЗОК(), ЛИНЕЙН()Выделить два столбца и пять строк, ввести формулу, нажать Ctrl+Shift+Enter

и пять строк, ввести формулу, нажать Ctrl+Shift+Enter

Слайд 21 Построение диаграммы и линии тренда
Выделить два столбца значений

Построение диаграммы и линии трендаВыделить два столбца значений X и Y

X и Y вместе с заголовками
Вставить точечную диаграмму (Тип

диаграммы – Точечная)

Выделить на диаграмме ряд
В контекстном меню выбрать Добавить линию тренда
Изменить параметры линии тренда (см. след слайд): Линейная (установлено по умолчанию), Показывать уравнение на диаграмме, Поместить на диаграмме величину достоверности аппроксимации R2

Слайд 22 Построение диаграммы и линии тренда

Построение диаграммы и линии тренда

Слайд 23 Анализ данных \ Регрессия

Анализ данных \ Регрессия

Слайд 24 Анализ данных \ Регрессия
Проверить, чтобы значения коэффициентов регрессии,

Анализ данных \ РегрессияПроверить, чтобы значения коэффициентов регрессии, найденные разными способами, совпадали!

найденные разными способами, совпадали!

Слайд 25 Вычислить коэффициент корреляции

Выборочная ковариация (функция КОВАРИАЦИЯ.В())


Коэффициент корреляции (функция

Вычислить коэффициент корреляцииВыборочная ковариация (функция КОВАРИАЦИЯ.В())Коэффициент корреляции (функция КОРРЕЛ(), Анализ данных \ Корреляция)

КОРРЕЛ(), Анализ данных \ Корреляция)

Слайд 26 Вычисление коэффициента корреляции

Вычисление коэффициента корреляции

Слайд 27 Оценить уровень значимости уравнения регрессии
Коэффициент детерминации

В случае одной

Оценить уровень значимости уравнения регрессииКоэффициент детерминацииВ случае одной независимой переменной XF-статистикаm

независимой переменной X

F-статистика
m – число параметров в уравнении регрессии,

(a0, a1 ), m = 2
(сравниваем с F.ОБР.ПХ(α = 0,05; k1 = m – 1; k2 = N – m = 23) = 4,28

Слайд 28 Сумма квадратов, обусловленная регрессией (RSS)
Сумма квадратов, обусловленная

Сумма квадратов, обусловленная регрессией (RSS)Сумма квадратов, обусловленная ошибкой (ESS)Общая сумма квадратов (TSS)Фактическая дисперсияОстаточная дисперсияВычислить

ошибкой (ESS)
Общая сумма квадратов (TSS)
Фактическая дисперсия
Остаточная

дисперсия

Вычислить

Слайд 29 Оценить значимость коэффициентов уравнения регрессии
Несмещенная оценка дисперсии остаточной

Оценить значимость коэффициентов уравнения регрессииНесмещенная оценка дисперсии остаточной компонентыdjj - диагональные

компоненты
djj - диагональные элементы матрицы C-1 (обратной матрицы системы

уравнений (*))

Стандартные ошибки коэффициентов уравнения регрессии

Стандартная ошибка оценки

t-статистика
СТЬЮДЕНТ.ОБР.2Х(α = 0,05; N – m = 23) = 2,069

Доверительный интервал

Слайд 30 Оценить значимость коэффициента корреляции

Оценить значимость коэффициента корреляции

Слайд 31 Найти доверительные интервалы для среднего и дисперсии

Найти доверительные интервалы для среднего и дисперсии

Слайд 32 Лабораторная работа № 5
Линейная регрессия для сгруппированных данных
Даны

Лабораторная работа № 5Линейная регрессия для сгруппированных данныхДаны две выборки, состоящие

две выборки, состоящие из K значений случайной величины X,

x1, x2, …, xK и M значений случайной величины Y y1, y2, …, yM . Каждая пара значений (xj, yi) встречается nji раз.







Построить уравнение регрессии

Метод наименьших квадратов

Слайд 33 Выполнение работы
Ввести исходные данные на рабочий лист Линейная

Выполнение работыВвести исходные данные на рабочий лист Линейная регрессия – сгруппированные

регрессия – сгруппированные данные
Для решения системы ввести матрицу коэффициентов

и правую часть системы, найти значения коэффициентов регрессии – решить систему с помощью функций МУМНОЖ(), МОБР()

Вспомогательный столбец H для расчета

Слайд 34 Выполнение работы
Сделать проверку

Выполнение работыСделать проверку

Слайд 35 Построить уравнение регрессии

Сделать самостоятельно по аналогии с п.

Построить уравнение регрессииСделать самостоятельно по аналогии с п. 1

Слайд 36 Вычислить коэффициент корреляции

Выборочная ковариация


Коэффициент корреляции
Примечания
При вычислении средних значений

Вычислить коэффициент корреляцииВыборочная ковариацияКоэффициент корреляцииПримечанияПри вычислении средних значений и средних квадратичных

и средних квадратичных отклонений использовать формулы для сгруппированных данных

(функции СРЗНАЧ()и СТАНДОТКЛОН.В() не подходят)
Ковариацию вычислить, используя вспомогательный столбец

Слайд 37 Сумма квадратов, обусловленная регрессией (RSS)
Сумма квадратов, обусловленная

Сумма квадратов, обусловленная регрессией (RSS)Сумма квадратов, обусловленная ошибкой (ESS)Общая сумма квадратов (TSS)Фактическая дисперсияОстаточная дисперсияВычислить

ошибкой (ESS)
Общая сумма квадратов (TSS)
Фактическая дисперсия
Остаточная

дисперсия

Вычислить

Слайд 38

Слайд 39 Лабораторная работа № 6
Множественная линейная регрессия
Даны три выборки,

Лабораторная работа № 6Множественная линейная регрессияДаны три выборки, состоящие из N

состоящие из N значений случайных величин X и Y

и Z , x1, x2, …, xN ; y1, y2, …, yN и z1, z2, …, zN .


Построить уравнение регрессии

Метод наименьших квадратов

Слайд 40 Выполнение работы
Ввести исходные данные на рабочий лист Множественная

Выполнение работыВвести исходные данные на рабочий лист Множественная линейная регрессия Для

линейная регрессия
Для решения системы ввести матрицу коэффициентов и

правую часть системы, найти значения коэффициентов регрессии – решить систему с помощью функций МУМНОЖ(), МОБР()

Вычислить коэффициенты регрессии при помощи функции ЛИНЕЙН()

Слайд 41 Анализ данных \ Регрессия

Анализ данных \ Регрессия

Слайд 42 Анализ данных \ Корреляция

Анализ данных \ Корреляция
  • Имя файла: ekonometrika.pptx
  • Количество просмотров: 75
  • Количество скачиваний: 0
- Предыдущая Одежда для школы
Следующая - Предельные углеводороды

Похожие презентации

Родительское собрание : На пути к подростковому возрасту (сценарий+презентация) консультация (3, 4 класс) по теме Родительское собрание : На пути к подростковому возрасту (сценарий+презентация) консультация (3, 4 класс) по теме 85
ОСОБЛИВОСТІ МЕТОДІВ НАВЧАННЯ ОСОБЛИВОСТІ МЕТОДІВ НАВЧАННЯ 110
Родительское собрание для родителей вновь прибывших детей. консультация Родительское собрание для родителей вновь прибывших детей. консультация 84
Музыка как наука воображения детей дошкольного возраста презентация Музыка как наука воображения детей дошкольного возраста презентация 87
Презентація Вона на світі одна-єдина , наша Україна Презентація Вона на світі одна-єдина , наша Україна 117
Венецианов Алексей Гаврилович Венецианов Алексей Гаврилович 89
Bellagio hotel Bellagio hotel 164
Домашние животные презентация Домашние животные презентация 174
День космонавтики презентация к уроку (подготовительная группа) День космонавтики презентация к уроку (подготовительная группа) 94
презентация Оформление группы новому году презентация к уроку (младшая группа) презентация Оформление группы новому году презентация к уроку (младшая группа) 98
Землепользование и землеустройство Землепользование и землеустройство 119
Интубация. Виды наркоза. Интубация. Виды наркоза. 92
Необычные свойства пирамид Необычные свойства пирамид 88
Основы теории формирования трудовых (технологических) умений Основы теории формирования трудовых (технологических) умений 124
Создание робота на плате Iskra JS, который управляется с помощью ИК-пульта Создание робота на плате Iskra JS, который управляется с помощью ИК-пульта 115
Определение мест негерметичности колонн и заколонных перетоков пластовых флюидов по данным ГИС Определение мест негерметичности колонн и заколонных перетоков пластовых флюидов по данным ГИС 99
Management enterprise Management enterprise 82
Презентация к уроку Ягоды югорского края презентация к уроку (3 класс) Презентация к уроку Ягоды югорского края презентация к уроку (3 класс) 109
Гамма - глутамилтрансфераза Гамма - глутамилтрансфераза 204
Моя родословная Моя родословная 133
Промышленная группа Фосфорит Промышленная группа Фосфорит 108
Мультимедийная презентация Сосудистая система Мультимедийная презентация Сосудистая система 96
Основы теории проверки статистических гипотез Основы теории проверки статистических гипотез 98
ФАЯНСОВАЯ ПОСУДА ФАЯНСОВАЯ ПОСУДА 174
Презентация для проведение праздника День именинника Презентация для проведение праздника День именинника 101
Фразеалогія Фразеалогія 135
Судебная защита прав супругов Судебная защита прав супругов 87
nemnogo tvorchestva i fantazii 2 nemnogo tvorchestva i fantazii 2 103
С Днем Учителя С Днем Учителя 133
Gerund and infinitive Gerund and infinitive 109