Слайд 2
Игра – одна из самых эффективных
методик обучения
детей
Существует огромное количество методик
и педагогических разработок для развития
логического мышления и интеллекта
ребенка. Часто в основе таких методик лежит
игра. Именно во время игры ребенок сам
включается в процесс познания и с легкостью
усваивает новое.
Слайд 3
Методика развития элементарных математических представлений у детей дошкольного
возраста постоянно развивается, совершенствуется, обогащается за счет новых технологий
обучения. Разработка и внедрение в практику эффективных дидактических средств, развивающих методов позволяет педагогам разнообразить занятия с детьми, познакомить со сложными, абстрактными математическими понятиями в доступной малышам форме.
Одним из таких дидактических средств являются счетные палочки Кюизенера.
Слайд 4
Палочки Кюизенера
Бельгийский учитель начальной школы Джордж Кюизенер (1891-1976)
разработал универсальный дидактический материал для развития у детей математических
способностей. В 1952 году он опубликовал книгу "Числа и цвета", посвященную своему учебному пособию.
Палочки Кюизенера – это набор счетных палочек, которые еще называют «числа в цвете», "цветными палочками", "цветными числами", "цветными линеечками". В наборе содержатся четырехгранные палочки 10 разных цветов и длиной от 1 до 10 см. Разработал Кюизенер палочки так, что палочки одной длины выполнены в одном цвете и обозначают определенное число. Чем больше длина палочки, тем большее числовое значение она выражает.
Слайд 5
Основные особенности этого дидактического материала - абстрактность, универсальность,
высокая эффективность.
Палочки Кюизенера
в наибольшей мере
отвечают
монографическому
методу обучения
числу и
счёту.
Слайд 6
Цель методики Кюизенера — использование принципа наглядности.
С
его помощью сложные абстрактные понятия из области элементарной математики
— числа, количественные величины, соотношения между ними — представлены в форме, которая максимально доступна детям. Это помогает научить ребёнка тем действиям, которые необходимы для закрепления в памяти простых, но важных математических понятий.
Слайд 7
Каждый цвет и каждая длина соответствуют определенному числу. Например,
палочка белого цвета – это куб со стороной 1см, она соответствует числу
-1;
палочка розового цвета – это прямоугольная призма длиной 2см и соответствует числу 2;
палочка оранжевого цвета – длиной 10см и соответствует числу 10.
Таким образом, все палочки в наборе различаются по трем признакам: цвет, длина и число, которому они соответствуют.
Данный материал представляет собой набор счетных палочек 10 разных цветов и разной длины от 1 до 10см. Комплектация набора не случайна, а является сложно продуманным математическим множеством.
Что же такое палочки Кюизенера?
Слайд 8
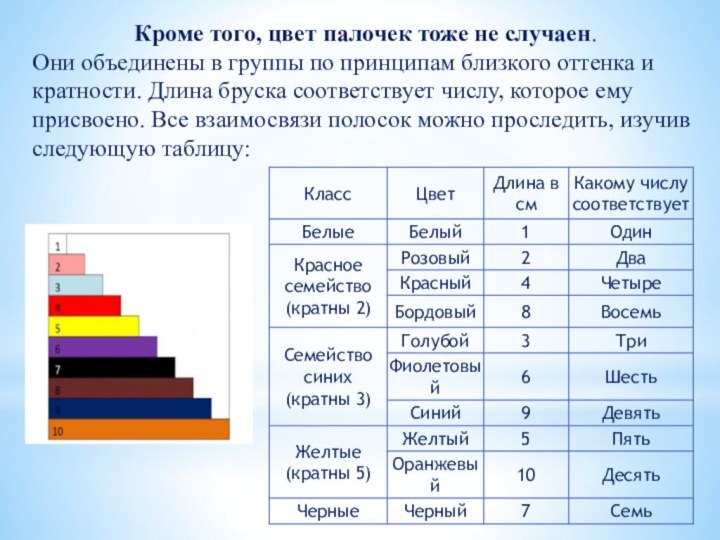
Кроме того, цвет палочек тоже не случаен.
Они объединены
в группы по принципам близкого оттенка и кратности. Длина
бруска соответствует числу, которое ему присвоено. Все взаимосвязи полосок можно проследить, изучив следующую таблицу:
Слайд 9
Цветные палочки позволяют решать
следующие задачи:
Познакомить с
понятием цвета (различать: цвет, классифицировать по цвету).
Познакомить с понятием
величины, длины, высоты, ширины (упражнять в сравнении предметов по высоте, длине, ширине).
Познакомить детей с последовательностью чисел натурального ряда.
Осваивать прямой и обратный счет.
Познакомить с составом числа.
Усвоить отношения между числами (больше — меньше, больше — меньше на...), пользоваться знаками сравнения.
Помочь овладеть арифметическими действиями сложения, вычитания, умножения и деления.
Развивать творческие способности, воображение, фантазию, способности к моделированию и конструированию.
Познакомить со свойствами геометрических фигур.
Развивать пространственные представления (слева, справа, выше, ниже)
Развивать логическое мышление, внимание, память.
Воспитывать самостоятельность, инициативу, настойчивость в достижении цели.
Слайд 10
Целесообразно организовывать развитие и обучение детей с использованием
палочек Кюизенера:
во-первых, вне занятий — наличие наборов палочек или
полосок в предметно-развивающей среде группы (математический центр);
во-вторых, в совместной и самостоятельной игровой деятельности (конструирование из палочек, моделирование цветными полосками);
в-третьих, на занятиях (комплексных, интегрированных), обеспечивающих наглядность, системность и доступность, смену видов деятельности.
Заниматься с палочками дети могут индивидуально или небольшими подгруппами в игровой деятельности, кроме того возможна и фронтальная работа со всей группой детей. Однако фронтальная работа не должна быть ведущей, так как накопление детского опыта происходит в повседневной детской деятельности, в игре. Важно осуществлять подбор игр, учитывая индивидуальные способности, возрастные возможности каждого ребенка, а также уровень развития детей.
Слайд 11
На начальном этапе занятий палочки Кюизенера
используются как игровой
материал. Дети играют с ними, как с обычными кубиками, палочками,
конструктором, по ходу игр и занятий, знакомясь с цветами, размерами и формами.
Слайд 12
Второй этап занятий палочки Кюизенера
Используются для работы по
схемам (выкладывание палочек на изображение), сначала с воспитателем, а
потом самостоятельно. Выкладываем свое изображение: фантазируем - домики, деревья, машинки, паровозики и пр.
Слайд 13
На третьем этапе
палочки уже выступают как пособие
для маленьких математиков. И тут дети учатся постигать законы
загадочного мира чисел и других математических понятий, изучают количественный состав, сколько палочек таких может уместиться в этой палочке, строим лесенки, какая палочка длиннее, какая короче.
Слайд 14
Примеры заданий на первом этапе:
Слайд 15
Схемы для палочек Кюизенера
Существует огромное количество схем. Их
нужно заполнять разноцветными брусочками полностью или частично. Еще можно
повторить рисунок на другой поверхности, а потом сравнивать фигуры. Схемы могут быть черно-белыми, разукрашенными. Занятия по ним развивают логическое и творческое детское мышление, навыки счета, представление цветов. Есть даже схемы, по которым можно создавать объемные сюжетные рисунки и даже целые фрагменты из волшебных сказок.
Второй этап
Слайд 16
Третий этап работы с палочками Кюизенера: математический
Цель:
Дети в буквальном смысле учатся «чувствовать» числа, то есть
обучение проходит не через абстрактные понятия, которые для ребенка пока очень расплывчаты, а через практику. - освоение сравнений и понятия части и целого.
Например, Чебурашка очень любит есть конфеты. Он может выбрать: либо полакомиться одной синей конфетой, но большой, либо большим количеством белых конфет, но маленьких. Какие конфеты выберет Чебурашка? Сколько белых конфет помещается в одну большую синюю?
Таким образом, мы ребенка подводим к азам счета.
Слайд 17
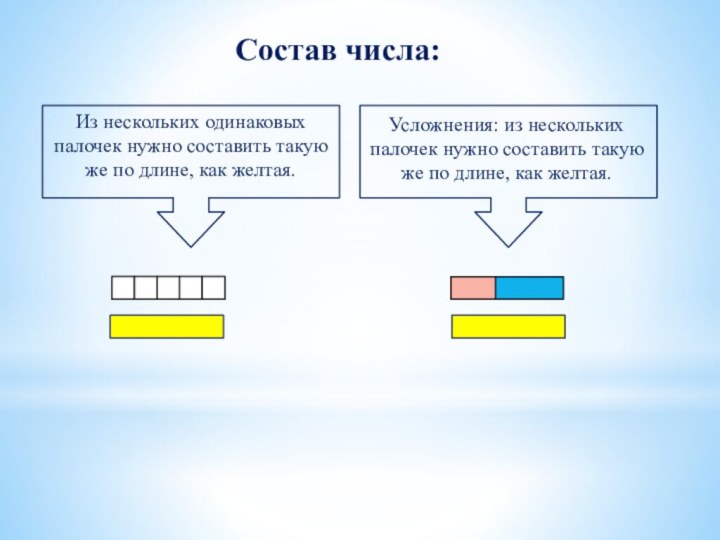
Состав числа:
Из нескольких одинаковых палочек нужно составить такую
же по длине, как желтая.
Усложнения: из нескольких палочек
нужно составить такую же по длине, как желтая.
Слайд 18
Примеры заданий на третий этапе
Выкладываем лесенку из 10
палочек от меньшей (белой) к большей (оранжевой) и наоборот.
Пройдитесь пальчиками по ступенькам лесенки, можно посчитать вслух от 1 до 10 и обратно.
Найти любую палочку, которая короче синей, длиннее красной.
Вы называете число — ребенок находит палочку соответствующего цвета. Вначале числа можно называть по порядку, далее — задача усложняется, числа идут вразбивку.
Слайд 19
Попросить составить два поезда. Первый из розовой и
фиолетовой, а второй из голубой и красной. Один поезд
состоит из голубой и красной палочки. Из белых палочек составь поезд длиннее имеющегося на 1 вагон.
С закрытыми глазами попросить взять любую палочку из коробки, посмотреть на нее и назовать ее цвет (позже можно определять цвет палочек даже с закрытыми глазами).
Положить синюю палочку между красной и желтой, а оранжевую слева от красной, розовую слева от красной.
Построить поезд из вагонов разной длины, начиная от самого короткого и заканчивая самым длинным. Спросить, какого цвета вагон стоит пятым, восьмым. Какой вагон справа от синего, слева от желтого. Какой вагон тут самый короткий, самый длинный? Какие вагоны длиннее желтого, короче синего.
Слайд 20
Методика Кюизенера – универсальна. Хотя палочки Кюизенера предназначены
непосредственно для обучения математике и объяснения математических концепций, они
оказывают дополнительное положительное воздействие на ряд пограничных областей: развивают мелкую моторику, зрительное и пространственное восприятие, стимулируют воображение, приучают к порядку.
Палочки Кюизенера просты и понятны детям: они привыкают к ним еще в совсем раннем возрасте и уже воспринимают в качестве игрового материала, а не видят в них скучное заучивание чисел.
Слайд 21
Недостатки методики Кюизенера
Практически все специалисты единогласно утверждают,
что недостатков у палочек Кюизенера нет. На сегодняшний день
этот дидактический материала является одним из самых лучших и действенных пособий, позволяющих с самого раннего возраста приобщать детей к математике. Мнение специалистов подтверждают и многочисленные восторженные отзывы родителей, которые уже практикуют занятия по методике Кюизенера в домашних условиях. Но, как известно, даже в мёде можно найти ложку дегтя. Не стали исключением и "цветные числа". Пресловутой "ложкой дегтя" можно считать необходимость систематических совместных (взрослого и ребёнка) занятий со
счетными палочками. В противном случае эффект
будет практически не заметен.