- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
Содержание
- 2. Локальная интерполяция 1. Кусочно–постоянная
- 4. Для правой кусочно-постоянной интерполяции
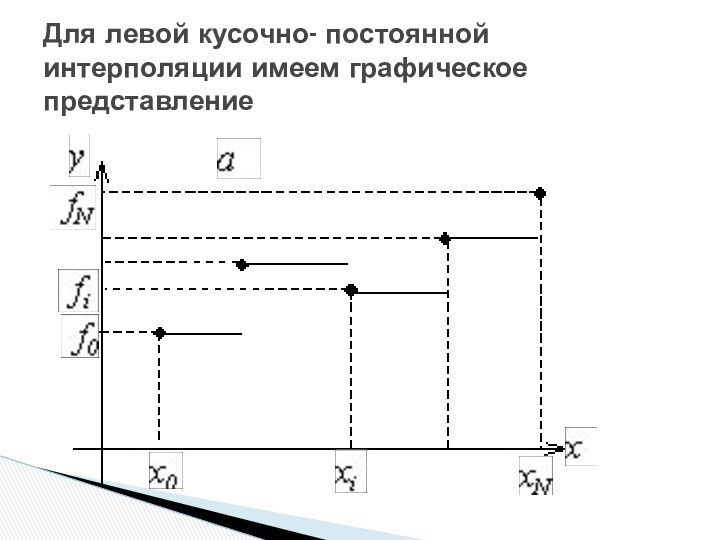
- 5. Для левой кусочно- постоянной интерполяции имеем графическое представление
- 6. На каждом интервале [xi–1, xi] функция является
- 7. Получаем систему уравнений: откуда находим
- 8. Следовательно, функцию F(z) можно записать в виде
- 9. Т.е.
- 10. Или F(x) = ki * (x
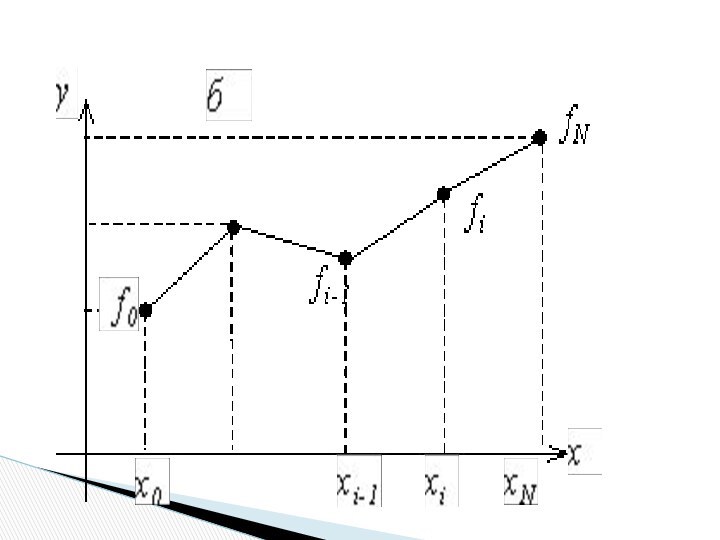
- 11. Иллюстрация кусочно–линейной интерполяции приведена на рисунке
- 13. Заданы значения некоторой функции:Пример:
- 14. Требуется найти значение функции при х=1 и
- 16. Точка х=3.2 принадлежит третьему интервалу [3, 3.5],
- 18. В случае глобальной интерполяции отыскивается единый полином
- 19. Допустим, что заданы две точки: (x0,f0) и
- 20. Для того, чтобы доказать это, выпишем систему
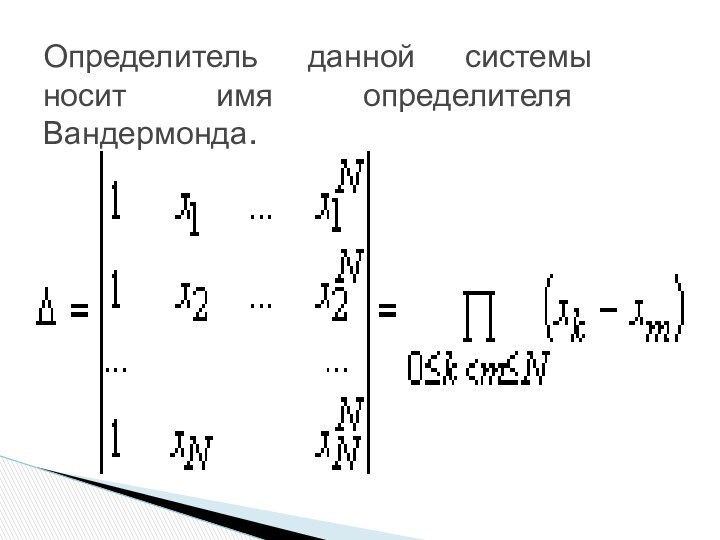
- 22. Определитель данной системы носит имя определителя Вандермонда.
- 23. Из курса математического анализа известно, что определитель
- 24. Решение ищем в виде где li(z) –
- 25. Убедимся в том, что если такие полиномы построены, то Ln(x) будет удовлетворять условиям интерполя-ции:
- 26. Каким образом построить базисные полиномы? Определимi=0,1,…, N
- 27. Легко понять, чтоФункция li(z) является полиномом N–й
- 28. i≠k;, т.е. k=1,…,i-1 или k=i+1,…,N.Таким образом, нам
- 30. Погрешность метода зависит от свойств исходной функции,
- 31. Рассмотрим частные случаи. Пусть N=1, т.е. заданы
- 32. т.е. получаем формулы кусочно–линейной интерполяции.
- 33. Пусть N=2. Тогда:В результате мы получили ф-лы квад-ратичной или параболической интерпо- ляции
- 34. Пример: Заданы значений неко-торой функции:Требуется найти значение
- 37. На каждом i–м отрезке [xi–1, xi], i=1,
- 38. • непрерывности первой и второй производной:S /i(xi–1)=S
- 39. ai=fi, i=1, 2,..., N, bi hi –
- 40. Недостающие два уравнения выводятся из дополнительных условий:
- 41. После этого вычисляются коэффициенты bi, di: i=1,
- 43. Данная CЛАУ имеет трехдиагональную матрицу и решается методом прогонки.Коэффициенты определяются из формул:
- 44. Для вычисления значения S(x) в произвольной точке
- 45. пример
- 46. Требуется вычислить значения функции в точках 0.25
- 48. Решая эту систему линейных уравнений, получим:
- 50. Рассмотрим точку 0.25, которая принадлежит первому отрезку, т.е. i=1. Следовательно, получим,
- 51. Рассмотрим точку 0.8, которая принадлежит четвертому отрезку, т.е. i=4.Следовательно,
- 52. Выполнить интерполяцию сплайнами третьей степени. Построить график и отметить на нем узлы интерполяции.пример
- 53. Построение интерполяционного многочлена в форме Ньютона применяется
- 54. Будем искать интерполяционный многочлен в виде:Pn(x)=a0+a1(x-x0)+a2(x-x0)(x-x1)+...+an(x-x0)(x-x1)...(x-xn-1)Найдем значения
- 55. a1=Δy0/ha2=Δ2y0/2!h2a3=Δ3y0/3!h3....................an=Δny0/n!hnТаким образом: Pn(x)=y0+ Δy0/h*(x-x0)+ Δ2y0/2!h2*(x-x0)(x-x1)+...+ Δny0/n!hn*(x-x0)(x-x1)...(x-xn-1) (1)
- 56. Практически формула (1) применяется в несколько ином
- 57. Построить интерполяционный многочлен Ньютона. Начертить график и
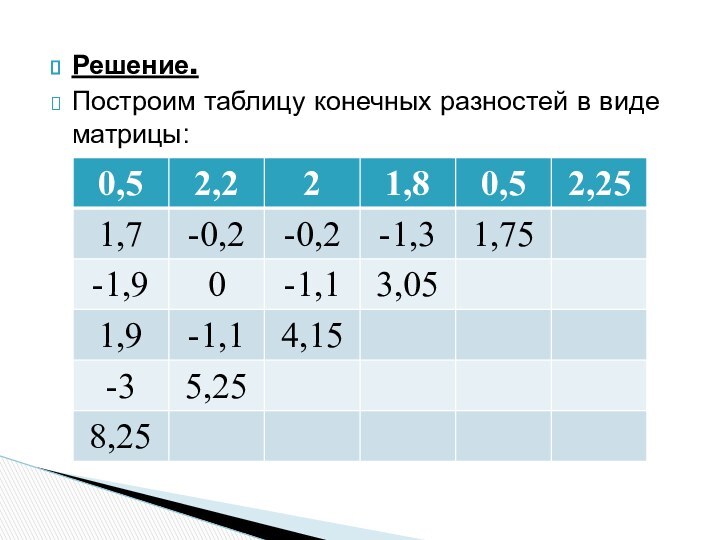
- 58. Решение.Построим таблицу конечных разностей в виде матрицы:
- 59. Скачать презентацию
- 60. Похожие презентации
Локальная интерполяция 1. Кусочно–постоянная интерполяция На каждом отрезке [xi-1,xi] интерполя-ционный многочлен равен константе , а именно левому или правому значе-нию функции. Для левой кусочно-постоянной интерполяции

![ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ Локальная интерполяция 1. Кусочно–постоянная интерполяция На каждом отрезке [xi-1,xi]](/img/tmb/14/1313807/0fbc3a776c04529e04cac9b2c18b9ab7-720x.jpg)
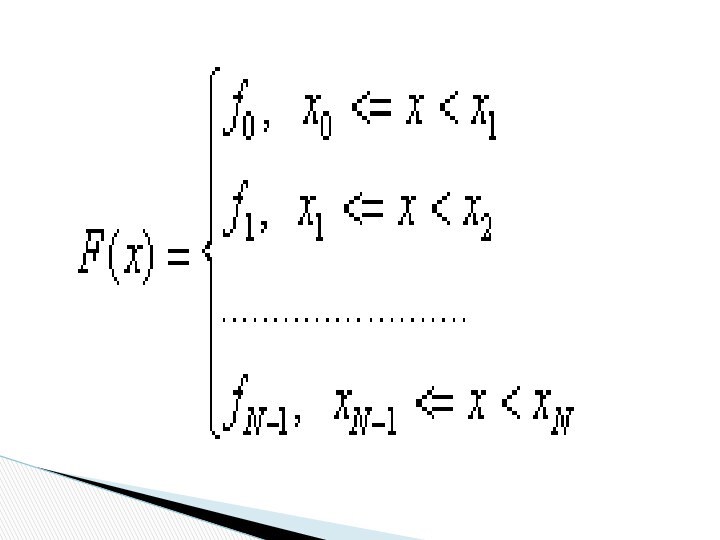

![ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ На каждом интервале [xi–1, xi] функция является линейной . Значения коэффициентов находятся](/img/tmb/14/1313807/3ee979dcb972330c4394e44cc0bdb01a-720x.jpg)







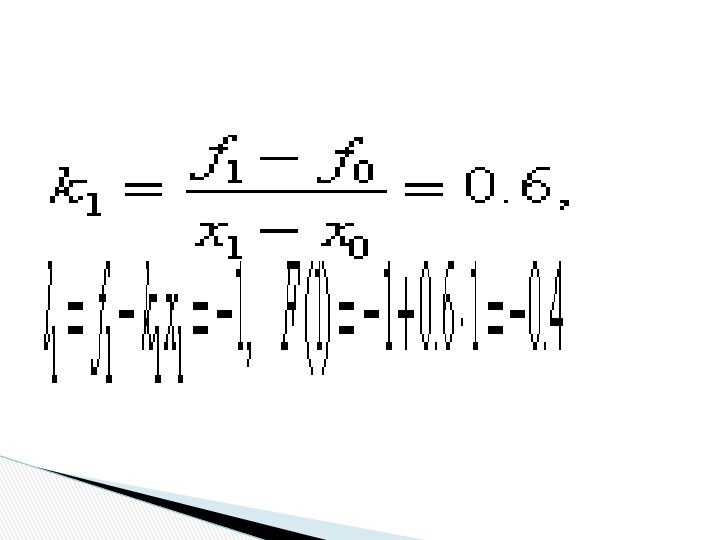
![ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ Точка х=3.2 принадлежит третьему интервалу [3, 3.5], т.е. и, следовательно, по формулам](/img/tmb/14/1313807/9c436af2d960209b8b3666493640f378-720x.jpg)

![ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ В случае глобальной интерполяции отыскивается единый полином на всём интервале [a, b],](/img/tmb/14/1313807/49a2f0c15008022580ce44b84a0d3ee1-720x.jpg)


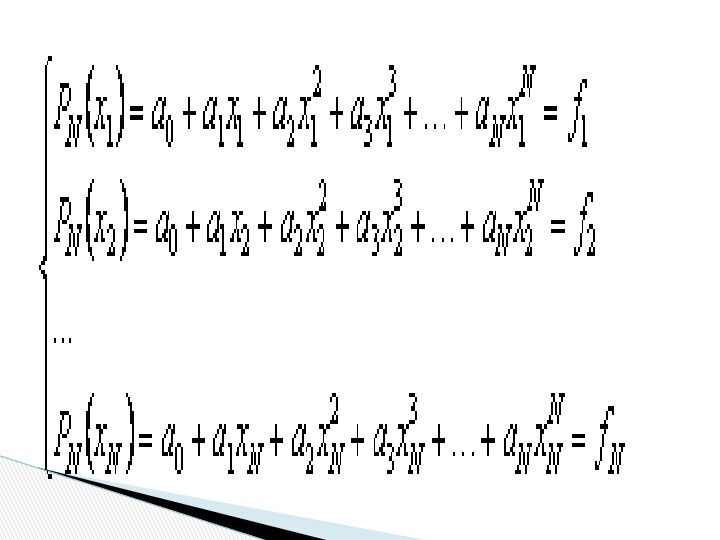






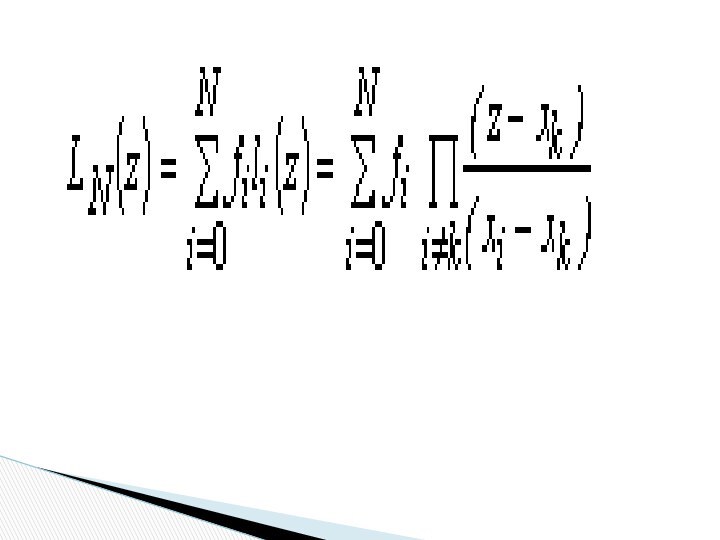





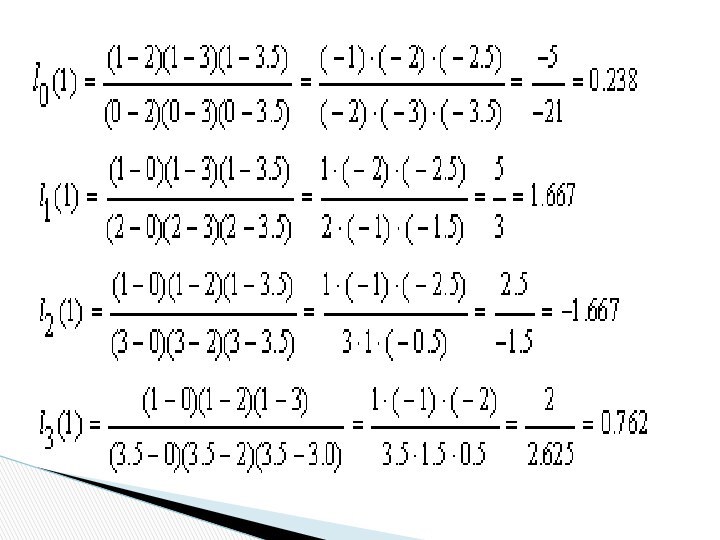
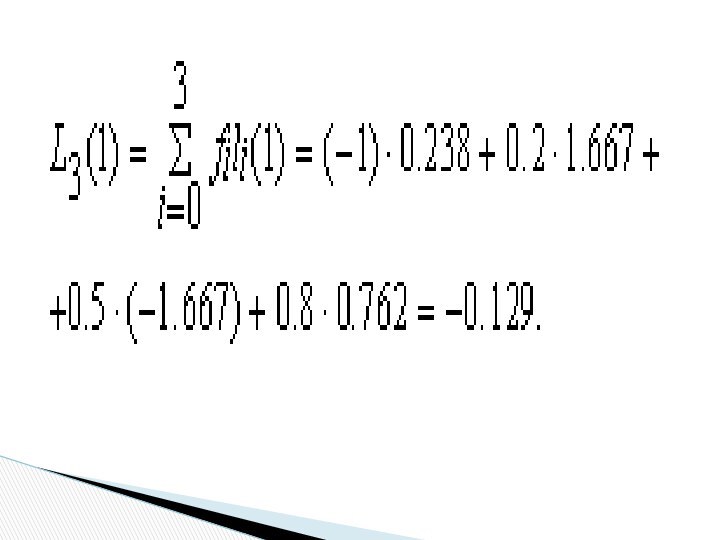
![ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ На каждом i–м отрезке [xi–1, xi], i=1, 2,…, N, решение будем искать](/img/tmb/14/1313807/0f43fe3866871ed4f9a07a5cb46cbd9f-720x.jpg)

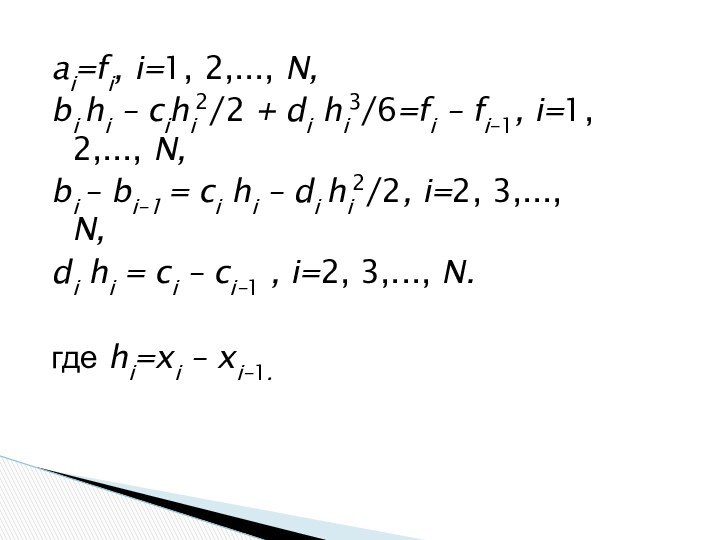

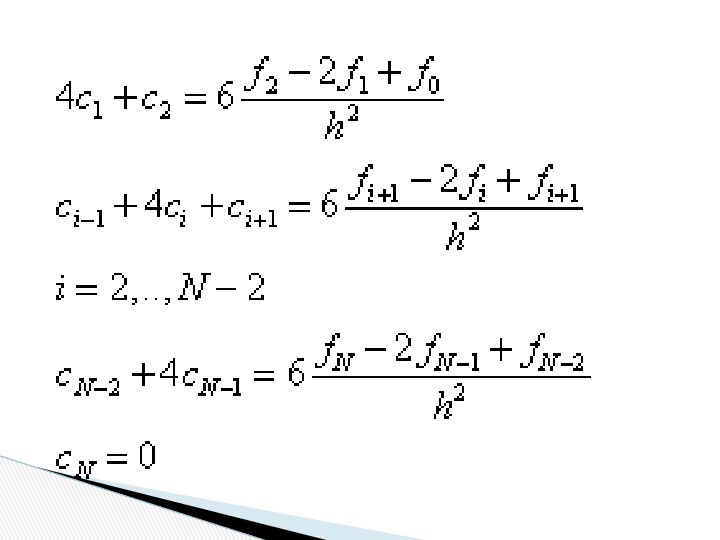

![ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ Для вычисления значения S(x) в произвольной точке отрезка z∈[a, b] необходимо решить](/img/tmb/14/1313807/07bca5eae3d88dcfead9c884f3118460-720x.jpg)

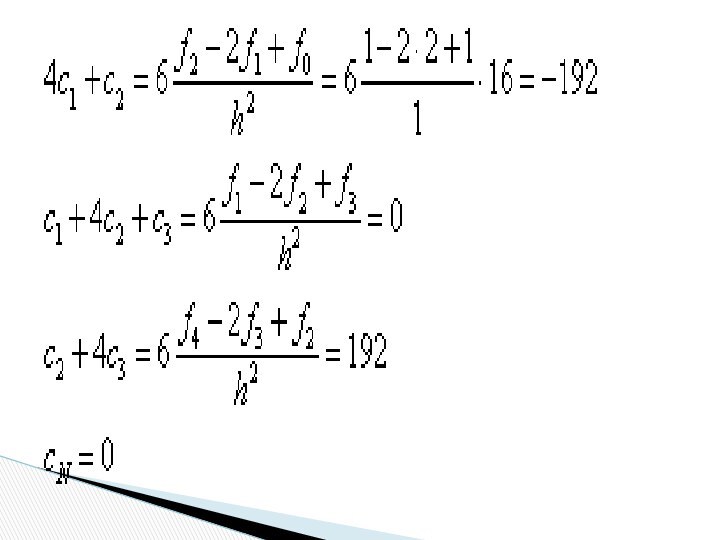

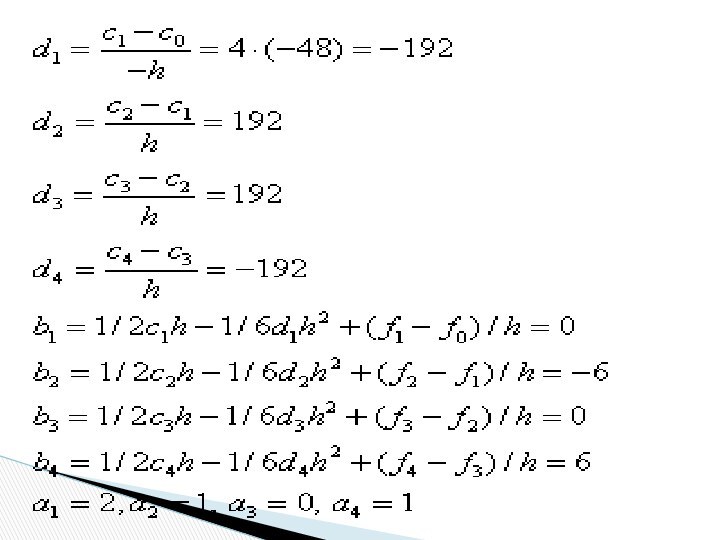









Слайд 6 На каждом интервале [xi–1, xi] функция является линейной
.
Значения коэффициентов находятся из выполнения условий интерполяции в
концах отрезка: Кусочно–линейная интерполяция
Слайд 10 Или F(x) = ki * (x -
xi-1) + fi-1, ki = (fi - fi-1) /
(xi - xi-1), xi-1 ≤ x ≤ xi, i=1,2,...,N-1При использовании линейной интерполяции сначала нужно определить интервал, в который попадает значение х, а затем подставить его в формулу. Итоговая функция будет непрерывной, но производная будет разрывной в каждом узле интерполяции.
Слайд 14 Требуется найти значение функции при х=1 и х=3.2
по кусочно–постоянной и кусочно–линейной интерполяции.
РЕШЕНИЕ.
Точка х=1 принадлежит первому
локальному отрезку [0, 2], т.е. i=1 и, следовательно, по формулам левой кусочно–постоянной интерполяции F(1) = f0 = –1, по формулам правой кусочно–постоянной интерполяции
F(1)=f1=0.2. Воспользуемся формулами кусочно–линейной интерполяции:
Слайд 16 Точка х=3.2 принадлежит третьему интервалу [3, 3.5], т.е.
и, следовательно, по формулам левой кусочно – постоянной интерполяции
F(3.2)= =0.5, по формулам правой кусочно – постоянной интерполяции F(3.2)= =0.8. Воспользуемся формулами кусочно–линейной интерполяции:Слайд 18 В случае глобальной интерполяции отыскивается единый полином на
всём интервале [a, b], т. е. строится полином, который
используется для интерполяции функции f(x) на всём интервале изменения аргумента х. Будем искать интерполирующую функцию в виде полинома (многочлена) m–ой степени Pm(x)=a0+a1x+a2x2+a3x3+…+am xm.Глобальная интерполяция
Слайд 19 Допустим, что заданы две точки: (x0,f0) и (x1,
f1), т.е. N=1. Через эти точки можно провести единственную
прямую, т.е. интерполирующей функцией будет полином первой степени P1(x)=a0+a1x. Через три точки (N=2) можно провести параболу P2(x)=a0+a1x+a2x2 и т.д. Рассуждая таким способом, можно предположить, что искомый полином должен иметь степень NСлайд 20 Для того, чтобы доказать это, выпишем систему уравнений
на коэффициенты. Уравнения системы представляют собой условия интерполяции при
каждом x=xiСлайд 23 Из курса математического анализа известно, что определитель отличен
от нуля, если xk≠xm (т. е. все узлы интерполяции
различные). Таким образом, доказано, что система имеет решение.Для нахождения коэффициентов а0, а1, а2, …, аn надо решить СЛАУ, что является сложной задачей. Но есть другой способ построения полинома N-ой степени, который не требует решения такой системы.
Слайд 24
Решение ищем в виде
где li(z) – базисные
полиномы N–й степени, для которых выполняется условие: .
Полином
Лагранжа
Слайд 25 Убедимся в том, что если такие полиномы построены,
то Ln(x) будет удовлетворять условиям интерполя-ции:
Слайд 27
Легко понять, что
Функция li(z) является полиномом N–й степени
от z и для нее выполняются условия "базисности":
=0
Слайд 28
i≠k;, т.е. k=1,…,i-1 или k=i+1,…,N.
Таким образом, нам удалось
решить задачу о построении интерполирующего полинома N-ой степени, и
для этого не нужно решать СЛАУ. Полином Лагранжа можно записать в виде:Слайд 30 Погрешность метода зависит от свойств исходной функции, а
также от расположения узлов интерполяции и точки z. Полином
Лагранжа имеет малую погрешность при небольших значениях N<20. При больших N погрешность начинает расти, что свидетельствует о том, что метод Лагранжа не сходится (т. е. его погрешность не убывает с ростом N).Слайд 31 Рассмотрим частные случаи. Пусть N=1, т.е. заданы значения
функции только в двух точках. Тогда базовые полиномы имеют
вид:
Слайд 33
Пусть N=2. Тогда:
В результате мы получили ф-лы квад-ратичной
или параболической интерпо-
ляции
Слайд 34
Пример: Заданы значений неко-торой функции:
Требуется найти значение функ-ции
при z=1, используя интерпо-ляционный полином Лагранжа. Для этого случая
N=3, т.е. полином Лагранжа имеет третий порядок. Вычислим значения базисных полиномов при z=1:Слайд 37 На каждом i–м отрезке [xi–1, xi], i=1, 2,…,
N, решение будем искать в виде полинома третьей степени:
Si(x)=ai+bi(x–xi)+ci(x–xi)2/2+di(x–xi)3/6
Неизвестные
коэффициенты ai, bi, ci, di, i=1, 2,..., N, находим из:• условий интерполяции: Si(xi)=fi, i=1, 2,..., N; S1(x0)=f0,
• непрерывности функции Si(xi–1)=Si–1(xi–1), i=2, 3,..., N,
Кубический интерполяционный сплайн
Слайд 38
• непрерывности первой и второй производной:
S /i(xi–1)=S /i–1(xi–1),
S //i(xi–1)=S //i–1(x i–1), i=2, 3,..., N.
Учитывая, что ,
для
определения 4N неизвестных получаем систему 4N–2 уравнений:
Слайд 39
ai=fi, i=1, 2,..., N,
bi hi – cihi2/2
+ di hi3/6=fi – fi–1, i=1, 2,..., N,
bi –
bi–1 = ci hi – di hi2/2, i=2, 3,..., N, di hi = ci – ci–1 , i=2, 3,..., N.
где hi=xi – xi–1.
Слайд 40 Недостающие два уравнения выводятся из дополнительных условий: S
//(a)=S //(b)=0. Можно показать, что при этом . Из
системы можно исключить неизвестные bi , di , получив систему N+1 линейных уравнений (СЛАУ) для определения коэффициентов ci:c0 =0, cN =0,
hici–1+2(hi+hi+1)ci+h i+1ci+1=6
i=1, 2,…, N–1. (1)
Слайд 41
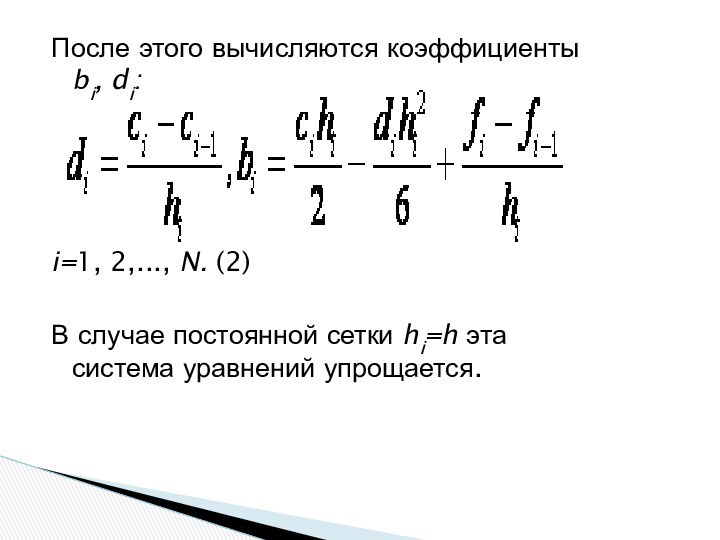
После этого вычисляются коэффициенты bi, di:
i=1, 2,...,
N. (2)
В случае постоянной сетки hi=h эта система уравнений
упрощается. Слайд 43 Данная CЛАУ имеет трехдиагональную матрицу и решается методом
прогонки.
Коэффициенты определяются из формул:
Слайд 44 Для вычисления значения S(x) в произвольной точке отрезка
z∈[a, b] необходимо решить систему уравнений на коэффициенты ci,
i=1,2,…, N–1, затем найти все коэффициенты bi, di. Далее, необходимо определить, на какой интервал [xi0, xi0–1] попадает эта точка, и, зная номер i0, вычислить значение сплайна и его производных в точке zS(z)=ai0 +bi0(z–xi0)+ci0(z–xi0)2/2+di0(z–x i0)3/6
S /(z)=bi0+ci0(z–xi0)+di0(z–x i0)2/2, S //(z)=ci0+di0(z–x i0).
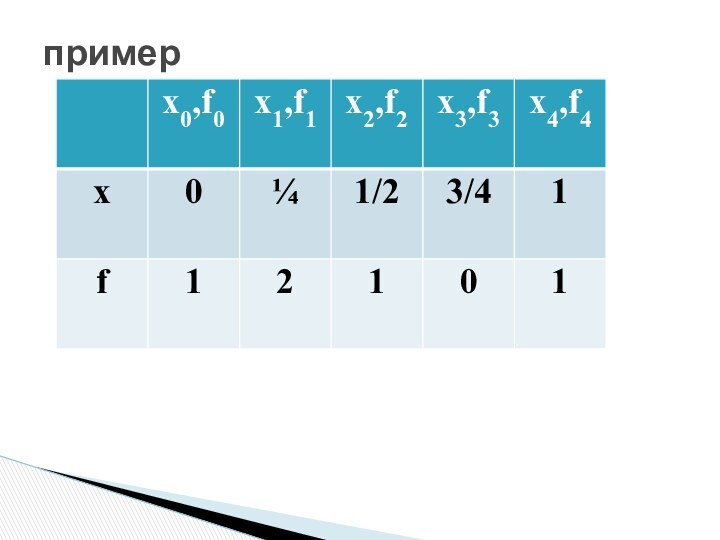
Слайд 46 Требуется вычислить значения функции в точках 0.25 и
0.8, используя сплайн – интерполяцию.
В нашем случае: hi=1/4,
Выпишем
систему уравнений для определения :
Слайд 50 Рассмотрим точку 0.25, которая принадлежит первому отрезку, т.е.
i=1. Следовательно, получим,
Слайд 52 Выполнить интерполяцию сплайнами третьей степени. Построить график и
отметить на нем узлы интерполяции.
пример
Слайд 53 Построение интерполяционного многочлена в форме Ньютона применяется главным
образом когда разность xi+1-xi=h постоянна для всех значений x=0..n-1.
Конечная
разность k-го порядка:Δyi=yi+1-yi
Δ2yi= Δyi+1- Δyi=yi+2-2yi+1+yi
………………………………
Δkyi=yi+k-kyi+1-k+k(k-1)/2!*yi+k-2+...+(-1)kyi
Интерполяционная формула Ньютона.
Слайд 54
Будем искать интерполяционный многочлен в виде:
Pn(x)=a0+a1(x-x0)+a2(x-x0)(x-x1)+...+an(x-x0)(x-x1)...(x-xn-1)
Найдем значения коэффициентов
a0, a1, a2, ...,an:
Полагая x=x0, находим a0=P(x0)=y0;
Далее подставляя значения
x1, x2, ...,xn получаем:
Слайд 55
a1=Δy0/h
a2=Δ2y0/2!h2
a3=Δ3y0/3!h3
....................
an=Δny0/n!hn
Таким образом:
Pn(x)=y0+ Δy0/h*(x-x0)+ Δ2y0/2!h2*(x-x0)(x-x1)+...+ Δny0/n!hn*(x-x0)(x-x1)...(x-xn-1)
(1)
Слайд 56
Практически формула (1) применяется в несколько ином виде.
Возьмем:
t=(x-x0)/h, тогда x=x0+th и формула (1) переписывается как:
Pn(x)=y0+tΔy0+t(t-1)/2! Δ2y0+...+t(t-1)...(t-n+1)/n!Δny0
(2)Формула (2) называется интерполяционной формулой Ньютона.
Слайд 57 Построить интерполяционный многочлен Ньютона. Начертить график и отметить
на нем узлы интерполяции. Вычислить значение функции в точке
х=1.25.пример





























